看資料結構寫程式碼(20)稀疏矩陣(順序儲存方式)
阿新 • • 發佈:2019-01-02
雜談:昨天辭職了,告別了繁重又無意義的工作。準備在家專心學習資料結構,好好磨練自己的基本功。
在寫這個小例子的時候遇到了 stack overflow(棧溢位)的問題,是 自己 分配了 過大的 棧變數,導致棧溢位。說實話,這還是 第一次 遇到,呵呵,別笑話我。看到網上的部落格在 說這個問題,還提起一些 作業系統術語,自己還真是 一知半解。好好努力,打好基本功吧。騷年。
進入正題:
當矩陣 的 有用資訊非常少時,我們考慮將矩陣壓縮儲存。這就涉及到 特殊矩陣 和 稀疏矩陣。
特殊矩陣 指的是 有一定規律的 矩陣,這個矩陣 我們 只儲存 部分 有用資訊,其餘的資訊 可以通過 公式 轉換 求得。例如 對稱矩陣,我們按行儲存主對角線以下(包括主對角線)的元素,其餘元素 我們可以通過 下面的公式求得。
稀疏矩陣,指的事沒有一定規律的矩陣,並且 有用資訊總數/矩陣總數 小於等於 0.05 的時候,我們稱之為 稀疏矩陣。
稀疏矩陣的表示方式有三種:1.三元組 2. 行邏輯連結順序表 3 .十字連結串列
前兩種 是 順序的儲存方式,第三種 是連結串列的儲存方式。
下面程式碼給出的 是行邏輯連結順序表的方式,這種方式 只是 比 三元組的 方式 多 了 一個存放 每行首元素位置的陣列,這樣使矩陣在矩陣乘法 和 矩陣 加減法 帶來了 很大的便利。
歡迎指出 程式碼 bug,下面上程式碼
// Sparse Matrix.cpp : 定義控制檯應用程式的入口點。 // //稀疏矩陣的順序儲存方式實現(行邏輯連結資料表) #include "stdafx.h" //#define MATRIX_MAX_SIZE 10000 //#define MATRIX_MAX_ROW 500 #define MATRIX_MAX_SIZE 100 #define MATRIX_MAX_ROW 50 enum E_State { E_State_Error = 0, E_State_Ok = 1, }; typedef int ElementType; //矩陣元素結構 struct MatrixData { int row;//行 int col;//列 ElementType data;//資料 }; struct SMatrix { MatrixData base[MATRIX_MAX_SIZE]; int rPos[MATRIX_MAX_ROW];//儲存每行第一個元素在陣列中的位置,並且保留了 最後一行的 邊界值 int rowNum;//行數 int colNum;//列數 int totalNum;//總數 }; void SMatrixInit(SMatrix * matrix,int * base,int row,int col){ matrix->rowNum = row; matrix->colNum = col; int totalNum = 0; for (int i = 0; i < row; i++) { int lastRowTotal = totalNum;//記錄從第一行到 上一行的總數 for (int j = 0; j < col; j++) { ElementType data = base[i*col+j]; if (data != 0) { matrix->base[totalNum].row = i; matrix->base[totalNum].col = j; matrix->base[totalNum].data = data; totalNum++; } } matrix->rPos[i] = lastRowTotal; } matrix->rPos[row] = totalNum;//為了 矩陣相乘,新增 邊界條件 matrix->totalNum = totalNum; } //普通轉置 時間複雜度 O(m.colNum * m.totalNum) //遍歷矩陣m,將第一列到 最後 一列 的矩陣元素加入到 t矩陣中 void SMatrixTranspose(SMatrix m,SMatrix * t){ t->totalNum = m.totalNum; t->rowNum = m.colNum; t->colNum = m.rowNum; int total = 0; for (int i = 0; i < m.colNum; i++) { for (int j = 0; j < m.totalNum; j++) { MatrixData data = m.base[j]; if (data.col == i) { t->base[total].row = data.col; t->base[total].col = data.row; t->base[total].data = data.data; total++; } } } } //快速轉置 時間複雜度為 O(m.totalNum + m.colNum) void SMatrixQuickTranspose(SMatrix m,SMatrix * t){ t->totalNum = m.totalNum; t->rowNum = m.colNum; t->colNum = m.rowNum; if (m.totalNum == 0) { return; } int col[MATRIX_MAX_ROW] = {0}; for (int i = 0; i < m.totalNum; i++)//計算矩陣m 每一列 的 元素個數 { MatrixData data = m.base[i]; col[data.col+1]++; } //計算 矩陣M 每一列 起始元素 在陣列中的位置 for (int i = 1; i < m.colNum; i++) { col[i] = col[i-1] + col[i]; } for (int i = 0; i < m.totalNum; i++) { MatrixData data = m.base[i]; int colBase = col[data.col]; t->base[colBase].col = data.row; t->base[colBase].row = data.col; t->base[colBase].data = data.data; col[data.col]++; } //最後設定 每行 首元素地址 t->rPos[0] = 0; for (int i = 1; i < t->rowNum; i++) { t->rPos[i] = col[i-1]; } } //矩陣相加 E_State SMatrixAdd(SMatrix m1,SMatrix m2,SMatrix * sum){ if (m1.rowNum != m2.rowNum || m1.colNum != m2.colNum) { return E_State_Error; } int totalNum = 0; sum->rowNum = m1.rowNum; sum->colNum = m1.colNum; for (int i = 0; i < m1.rowNum; i++) { int m1Start = m1.rPos[i]; int m1End = m1.rPos[i+1]; int m2Start = m2.rPos[i]; int m2End = m2.rPos[i+1]; sum->rPos[i] = totalNum; while (m1Start < m1End && m2Start < m2End) { MatrixData m1Data = m1.base[m1Start]; MatrixData m2Data = m2.base[m2Start]; int m1Col = m1Data.col; int m2Col = m2Data.col; if (m1Col == m2Col)//相等 { int sumData =m1Data.data + m2Data.data; if (sumData != 0) { sum->base[totalNum].row = i; sum->base[totalNum].col = m1Col; sum->base[totalNum].data = sumData; totalNum++; } m1Start++; m2Start++; } else if (m1Col < m2Col)//m2 的列 大 { sum->base[totalNum].row = i; sum->base[totalNum].col = m1Col; sum->base[totalNum].data = m1Data.data; totalNum++; m1Start++; } else//m1的列大 { sum->base[totalNum].row = i; sum->base[totalNum].col = m2Col; sum->base[totalNum].data = m2Data.data; totalNum++; m2Start++; } } while (m1Start < m1End) { MatrixData m1Data = m1.base[m1Start]; int m1Col = m1Data.col; sum->base[totalNum].row = i; sum->base[totalNum].col = m1Col; sum->base[totalNum].data = m1Data.data; totalNum++; m1Start++; } while (m2Start < m2End) { MatrixData m2Data = m2.base[m2Start]; int m2Col = m2Data.col; sum->base[totalNum].row = i; sum->base[totalNum].col = m2Col; sum->base[totalNum].data = m2Data.data; totalNum++; m2Start++; } } sum->rPos[sum->rowNum] = totalNum; sum->totalNum = totalNum; return E_State_Ok; } //矩陣相減 E_State SMatrixSub(SMatrix m1,SMatrix m2,SMatrix * sub){ if (m1.rowNum != m2.rowNum || m1.colNum != m2.colNum) { return E_State_Error; } for (int i = 0; i < m2.totalNum; i++) { m2.base[i].data = -m2.base[i].data; } E_State state = SMatrixAdd(m1,m2,sub); return state; } //矩陣相乘 E_State SMatrixMult(SMatrix m1,SMatrix m2,SMatrix * result){ if (m1.colNum != m2.rowNum)//排除不合法的情況.. { return E_State_Error; } result->rowNum = m1.rowNum; result->colNum = m2.colNum; result->totalNum = 0; if (m1.totalNum * m2.totalNum != 0) { for (int m1Row = 0; m1Row < m1.rowNum; m1Row++) { int m1End = m1.rPos[m1Row+1]; int colCount[MATRIX_MAX_ROW] = {0}; for (int m1Start = m1.rPos[m1Row]; m1Start < m1End; m1Start++) { MatrixData m1Data = m1.base[m1Start]; int col = m1Data.col; for (int m2start = m2.rPos[col]; m2start < m2.rPos[col+1]; m2start++) { MatrixData m2Data = m2.base[m2start]; colCount[m2Data.col] += m1Data.data * m2Data.data; } } result->rPos[m1Row] = result->totalNum; for (int col = 0; col < m2.colNum; col++) { if (colCount[col] != 0) { result->base[result->totalNum].col = col; result->base[result->totalNum].row = m1Row; result->base[result->totalNum].data = colCount[col]; result->totalNum ++; } } } result->rPos[result->rowNum] = result->totalNum; } return E_State_Ok; } //遍歷矩陣 void SMatricTraverse(SMatrix matrix){ int rowNum = 0; printf("--------------遍歷開始------------------------\n"); for (int i = 0; i < matrix.totalNum; i++) { MatrixData data = matrix.base[i]; printf("%d行 %d列 : %d\n",data.row+1,data.col+1,data.data); } printf("--------------遍歷結束------------------------\n"); } int initData[5][10] = { {1,0,0,0,0,0,0,0,0,0}, {0,0,2,0,0,0,0,0,5,0}, {0,0,0,3,0,0,0,0,0,0}, {0,2,0,0,0,0,0,0,0,0}, {1,0,0,0,0,0,0,0,0,9}, }; int initAddData[5][10]= { {1,0,0,0,3,0,0,0,0,0}, {0,0,2,0,4,0,0,0,5,0}, {0,0,0,3,0,0,0,0,0,0}, {0,2,0,0,2,0,0,0,0,0}, {1,0,0,0,1,0,0,0,0,9}, }; int initData2 [10][2] = { {1,0}, {0,0}, {0,0}, {0,0}, {0,0}, {0,6}, {0,0}, {0,0}, {5,0}, {0,0}, }; int _tmain(int argc, _TCHAR* argv[]) { SMatrix matrix; SMatrixInit(&matrix,(int *)initData,5,10); SMatricTraverse(matrix); printf("--------------普通轉置-----------------------\n"); SMatrix tMatrix; SMatrixTranspose(matrix,&tMatrix); SMatricTraverse(tMatrix); printf("--------------快速轉置-----------------------\n"); SMatrix qtMatrix; SMatrixQuickTranspose(matrix,&qtMatrix); SMatricTraverse(qtMatrix); printf("--------------矩陣相乘-----------------------\n"); SMatrix m2; SMatrixInit(&m2,(int *)initData2,10,2); SMatrix mul; SMatrixMult(matrix,m2,&mul); SMatricTraverse(mul); printf("--------------矩陣相加-----------------------\n"); SMatrix mAdd; SMatrixInit(&mAdd,(int *)initAddData,5,10); SMatrix mSum; SMatrixAdd(matrix,mAdd,&mSum); SMatricTraverse(mSum); printf("--------------矩陣相減-----------------------\n"); SMatrix mSub; SMatrixSub(matrix,mAdd,&mSub); SMatricTraverse(mSub); return 0; }
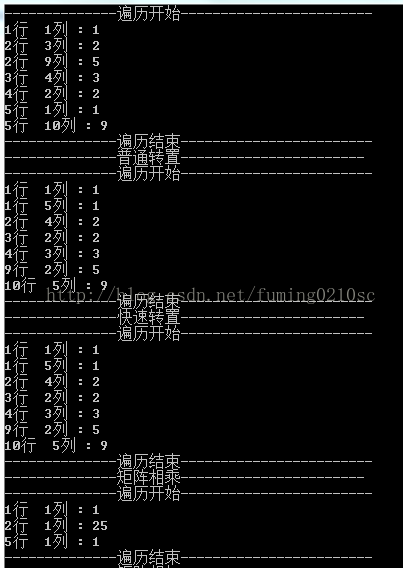
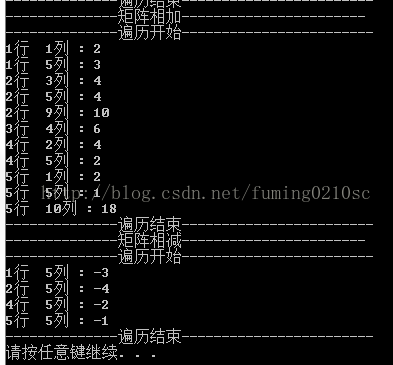
執行程式碼,截圖