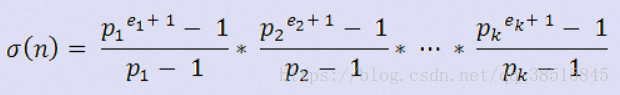這道題我很久以前寫過一篇部落格，這裡就不再討論，做法就是尤拉函式打表然後二分查詢（據說暴力查詢也行？）即可。

這題表示目前還不會，看題解似乎與二分圖有關。。。知識盲區，估計挺久以後才有時間補

題意大致是對給定的a、b，求滿足x*y==a&&x>=b&&y>=b&&x<y的(x,y)的個數。

我的解法是先線性篩打1e6的素數表，當b>sqrt(a)||b*b==a時顯然沒有滿足條件的(x,y)，ans=0；而當b<=sqrt(a)時，利用素數表把a分解質因數，再對質因數暴搜尋找符合條件的值，每找到一 個滿足x>=sqrt(b)&&x*x!=a&&x<=sqrt(a)的x就ans++，因為x*y==a，所以y一定大於sqrt(a)，也就大於b。

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define N 1000002
int t,ans;
ll a,b;
bool notprime[N];
int prime[100005],cnt;
void init(){
	notprime[1]=true;
	for(int i=2;i<N;i++){
		if(!notprime[i])
		prime[cnt++]=i;
		for(int j=0;j<cnt&&i*prime[j]<N;j++){
			notprime[i*prime[j]]=true;
			if(i%prime[j]==0)
			break;
		}
	}
}
int pcnt,e[105];
ll p[105];
void fenjie(ll x){//把x分解為p[0]^e[0] * p[1]^e[1] * ... * p[pcnt-1]^e[pcnt-1]
	pcnt=0;
	memset(e,0,sizeof(e));
	for(int i=0;i<cnt&&prime[i]<=x;i++){
		if(x%prime[i]==0){
			p[pcnt]=prime[i];
			while(x%prime[i]==0)
			x/=prime[i],e[pcnt]++;
			pcnt++;
		}
	}
	if(x>1){
		p[pcnt]=x,e[pcnt++]++;
	}	
}
void dfs(int now,ll s){//通過分解的質因數列舉x的因子，不懂的可能需要了解一下算術基本定理
	if(s>sqrt(a))//若當前列舉的因子s已經大於sqrt(a)，顯然之後所有情況也不符合條件，剪掉
	return;
	if(now==pcnt){//列舉完所有素因子的個數後，判斷s是否符合條件
		if(s>=b&&(s*s)!=a)
			ans++;
		return;
	}
	for(int i=0;i<=e[now];i++){//列舉因子s中素因子p[now]的個數
		if(i==0)
		s*=1;
		else
		s*=p[now];
		dfs(now+1,s);
	}
}
int main(){
	init();
	cin>>t;
	int cas=0;
	while(t--){
		scanf("%lld %lld",&a,&b);
		ans=0;
		if(b<=(int)sqrt(a)){
			fenjie(a);
			dfs(0,1);
		} 
		cout<<"Case "<<++cas<<": "; 
		cout<<ans<<"\n";
	}
	return 0;
}
 

題意大致是定義了一個sigma(n)（如下圖），對給定的n，需要求從i從1到n所有的sigma(i)中偶數的個數。

首先我們可以把這個式子化一下，變成sigma(n)=(p1-1)*(p1^e1+p1^(e1-1)+...+1)/(p1-1)*...*(pk-1)*(pk^ek+pk^(ek-1)+...+1)/(pk-1)，約去分母，即為sigma(n)=(p1^e1+p1^(e1-1)+...+1)*...*(pk^ek+pk^(ek-1)+...+1)。

從這個式子可以發現，當n含有的除了2以外的素因子的冪次只要有一個為奇數時sigma(n)就為偶數。

為什麼呢？首先，除了2以外的素因子都是奇數，奇數的任意次冪均為奇數，奇數的0次冪，假設奇數的k次冪到0次冪的和為奇數，則奇數的k+1次冪到0次冪的和為 (奇數)+(奇數的k+1次冪)，顯然是偶數，即奇數的奇數次冪到0次冪的和為偶數。而偶數乘以任何數都是偶數，因此滿足上述條件的sigma(n)為偶數。

然後逆向思考一下，什麼情況下sigma(n)不為偶數？自然就是除了2以外的素因子的冪次全部都是偶數的時候啦！這不就是平方數嘛！當然，我們還需要考慮一下素因子2，因為它是個偶數，所以導致除了考慮平方數以外還需要考慮它們的2倍（不需要考慮4倍是因為 (平方數)*4也是平方數，避免重複計數）！因此，對於給定的n，1到n中sigma(i)為偶數的個數有n-sqrt(n)-sqrt(n/2)。

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define For(i,a,b) for(int i=a;i<=b;i++)
#define INF 0x3f3f3f3f
#define N 1005
#define db double;
int t;
ll n,ans;
int main(){
	cin>>t;
	int cas=0;
	while(t--){
		cin>>n;
		ans=0;
		ans+=(ll)sqrt(n),ans+=(ll)sqrt(n/2),ans=n-ans;
		cout<<"Case "<<(++cas)<<": "<<ans<<endl;
	}
	return 0;
}

題目大意是對於給定的n和k，求出n^k的最高的三位數字和最低的三位數字。這題似乎和我寫過的xdoj1029 數一的逆襲有點像。

首先，求低三位很簡單嘛，就是((n%1000)^k)%1000，直接上快速冪。

那麼，求高三位該怎麼辦呢？高精度暴力乘法？肯定超時。這時候我們想到了利用浮點數。假設x=n^k，y=log10(n^k)=klog10(n)，令y1=(int)y，y2=y-y1，可知x=10^(y1+y2)=(10^y1)*(10^y2)，10^y1只有x的最高位是1，其他位全是0，即每一位的數值是什麼由10^y2確定，且10^y2的值為1.多，因此我們只需要求出(int)((10^y2)*100)即為高三位的值。

#include<iostream>
#include<cmath>
#include<string>
#include<algorithm>
using namespace std;
int t,n,k;
string aans;
#define db double
void qpow(int x,int y,int p){
	aans.clear();
	int ans=1;
	while(y){
		if(y&1) ans=ans*x%p;
		y>>=1;
		x=x*x%p;
	}
	int tt=ans;
	while(ans){
		aans+=(ans%10+'0');
        ans/=10;
 	}
 	if(tt==0)//需要注意的是末三位的輸出格式，需用前導0補齊三位，這裡我寫的比較麻煩且無腦
 	aans+="0";
     if(tt<10){
		aans+="00";
	}
	else if(tt<100){
		aans+="0";
	}
	reverse(aans.begin(),aans.end());
}
int main(){
	cin>>t;
	for(int cas=1;cas<=t;cas++){
		cin>>n>>k;
		cout<<"Case "<<cas<<": ";
		db ans=k*log10(n);
		qpow(n%1000,k,1000);
		cout<<(int)(pow(10,ans-(int)ans)*100)<<" "<<aans<<endl;
	}
	return 0;
}

題目與哥德巴赫猜想有關，還記得之前寧夏邀請賽網賽的時候寫一道哥德巴赫猜想的題因為溢位T成了傻逼。

題意：對給定的n，求滿足a<=b&&a+b==n的素數(a,b)的對數。

受網賽那題的影響，還有空間大小計算失誤，以為1e7素數表打不了，開始居然寫了個miller_rabbin素數測試，成功的T了。。。然後再次計算了空間大小，轉為素數篩，對每個n列舉素數a，通過bool陣列O(1)判b即可。

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define For(i,a,b) for(int i=a;i<=b;i++)
#define INF 0x3f3f3f3f
#define N 10000004
#define db double;
int n,t,cnt,prime[800005],y,ans;//這裡一個小技巧，先本地陣列開大一點，打完表看究竟有多少個，再將陣列儘量開小，直接1e7會爆空間
bool notprime[N+1];
void init(){
	notprime[1]=true;
	For(i,2,N){
		if(!notprime[i]) prime[cnt++]=i;
		for(int j=0;j<cnt&&prime[j]*i<=N;j++){
			notprime[prime[j]*i]=true;
			if(i%prime[j]==0){
				break;
			}
		}
	}
}

int main(){
	init();
	int cas=0; 
	cin>>t;
	while(t--){
		ans=0;
		cin>>n;
		for(int j=0;prime[j]<=n/2;j++){
			y=n-prime[j];
			if(notprime[y]==0) ans++;
		}
		cout<<"Case "<<(++cas)<<": "<<ans<<"\n";
	}
	return 0;
}

大意：定義H(n)=sigma(n/i)（i從1到n）,對給定的n求H(n)。

我們可以把i以sqrt(n)為分界進行考慮，對於小於等於sqrt(n)的i，n/i的值各不相同，需要一個個列舉i來得到n/i的值；

對於大於等於sqrt(n)的i，n/i的個數為n/(n/i)-n/(n/i+1)，因為很多都是相同的，所以沒必要一個個列舉i，可以通過列舉n/i的值解決，因為i大於等於sqrt(n)，所以n/i小於等於sqrt(n)。注意當n/i==i時會重複計數，需要特判。

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define For(i,a,b) for(int i=a;i<=b;i++)
#define INF 0x3f3f3f3f
#define N 50005
#define db double;
int n,t,p[N],cnt,y;
ll ans=0;
template<class T>
inline bool scan_d(T &ret){
	char c;
	int sgn;
	if(c=getchar(),c==EOF) return 0;
	while(c!='-'&&(c<'0'||c>'9')) c=getchar();
	sgn=(c=='-')?-1:1;
	ret=(c=='-')?0:(c-'0');
	while(c=getchar(),c>='0'&&c<='9') ret=ret*10+c-'0';
	ret*=sgn;
	return 1;
}
int main(){
	scan_d(t);
	For(cas,1,t){
		scan_d(n);
		int sn=sqrt(n);
		ans=0;
		for(int i=1;i<=sn;i++){
			ans+=(n/i-n/(i+1))*1ll*i+n/i;
			if(n/i==i)
			ans-=i;
		}
		printf("Case %d: %lld\n",cas,ans);
	}
	return 0;
}

題意：對於給定的n，求有多少對(i,j)（i從1到n，j從1到n，i<=j)，滿足i和j的最小公倍數為n。

這題主要用到算術基本定理。將n分解質因數，可知，i和j的最小公倍數為n，則i和j只能含有n所含有的質因子，且i和j中至少有一個數該質因子的冪次為n中該質因子的冪次。

假設n分解為p1^e1 * p2^e2 * ... * pk^ek，先拋開i<=j這個條件，總情況數為(2*e1+1)*(2*e2+1)*...*(2*ek+1)——對於每個質因子， 先選定i或j其中一個為e次冪，另一個則可以從0到e次冪，因此為2*(e+1)，又因為兩個都是e的情況計算了兩次，所以減1，再把所有素因子的情況乘起來。

再考慮i<=j，因為i<j和i>j是完全對稱的，i==j只有i=j=n一種情況，那麼只需要去掉對稱的一半情況數即可。

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define For(i,a,b) for(int i=a;i<=b;i++)
#define INF 0x3f3f3f3f
#define N 10000005
#define db double
int t;
ll n,ans;
template<class T>
inline bool scan_d(T &ret){
	char c;
	int sgn;
	if(c=getchar(),c==EOF) return 0;
	while(c!='-'&&(c<'0'||c>'9')) c=getchar();
	sgn=(c=='-')?-1:1;
	ret=(c=='-')?0:(c-'0');
	while(c=getchar(),c>='0'&&c<='9') ret=ret*10+c-'0';
	ret*=sgn;
	return 1;
}
bool notprime[N];
int cnt,prime[1000005];
void init(){
	notprime[1]=true;
	For(i,2,10000001){
		if(!notprime[i]) prime[cnt++]=i;
		for(int j=0;j<cnt&&prime[j]*i<=10000001;j++){
			notprime[prime[j]*i]=true;
			if(i%prime[j]==0)
			break;
		}
	}
}
int p[205],e[205],pcnt;
void fenjie(ll x){
	pcnt=0,ans=1;
	memset(e,0,sizeof(e));
	for(int i=0;i<cnt&&prime[i]<=x;i++){
		if(x%prime[i]==0){
			p[pcnt]=prime[i];
			while(x%prime[i]==0){
				e[pcnt]++;
				x/=prime[i];
			}
			ans*=(2*e[pcnt++]+1);
		}
	}
	if(x>1){
		p[pcnt]=x,e[pcnt]++;
		ans*=(2*e[pcnt++]+1);
	}
	cout<<(ans-1)/2+1<<"\n";
}
int main(){
	init();
	scan_d(t);
	For(cas,1,t){
		scan_d(n);
		cout<<"Case "<<cas<<": ";
		fenjie(n);
	}
	return 0;
}

題意：對給定n求Hn。

這題想了挺久的，總感覺除了暴力沒啥好方法，但是陣列又開不下。。。這可咋整。

還好靈光一閃，想到了分割槽間打表（以前從來沒見過這玩意，  所以自己琢磨了很久才想到）。方法就是將很大的資料量分為多個區間，比如本題至多1e8，可分為1e6個區間，每個區間也就是100個數，只需要存下每個區間的第一個數，查詢的時候就能在100次以內推出答案。

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define For(i,a,b) for(int i=a;i<=b;i++)
#define INF 0x3f3f3f3f
#define N 1000005
#define db double
int n,m,t,mm;
db ans;
template<class T>
inline bool scan_d(T &ret){
	char c;
	int sgn;
	if(c=getchar(),c==EOF) return 0;
	while(c!='-'&&(c<'0'||c>'9')) c=getchar();
	sgn=(c=='-')?-1:1;
	ret=(c=='-')?0:(c-'0');
	while(c=getchar(),c>='0'&&c<='9') ret=ret*10+c-'0';
	ret*=sgn;
	return 1;
}
db f[N];
void init(){
	int tt; 
	for(int i=1;i<=100000000;i++){
		if(i%100==1){
			tt=i/100+1;
			f[tt]=f[tt-1];
		}
		f[tt]+=1.0/i;
	}
}
int main(){
	init();
	scan_d(t);
	For(cas,1,t){
		scan_d(n);
		m=n/100;
		mm=n-100*m;
		ans=f[m];
		For(i,n-mm+1,n){
			ans+=1.0/i;
		}
		printf("Case %d: %.10f\n",cas,ans);
	}
	return 0;
}

題意：對於給定x，x=y^k，求k的最大值。

算術基本定理分解質因數。。。對所有質因數的冪次求gcd即可。需要注意的是x為負數的情況，可以先去掉負號，與正數一樣  處理，這時候若gcd為偶數，則需將gcd除2直到gcd為奇數為止。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
#define ll long long
#define N 100005
ll t,n,prime[N],cnt,ans;
bool notprime[N];
void init(){
	notprime[1]=true;
	for(int i=2;i<N;i++){
		if(!notprime[i]) prime[cnt++]=i;
		for(int j=0;j<cnt&&prime[j]*i<N;j++){
			notprime[prime[j]*i]=true;
			if(i%prime[j]==0)
			break;
		}
	}
}
ll p[205],e[205],pcnt;
void fenjie(ll x){
	memset(e,0,sizeof(e));
	pcnt=0;
	for(int i=0;i<cnt&&prime[i]<=x;i++){
		if(x%prime[i]==0){
			p[pcnt]=prime[i];
			while(x%prime[i]==0){
				x/=prime[i];
				e[pcnt]++;
			}
			pcnt++;
		}
	}
	if(x>1)
	p[pcnt]=x,e[pcnt++]++;
}
int main(){
	init();
	cin>>t;
	for(int cas=1;cas<=t;cas++){
		cin>>n;
		bool flag=0;
		if(n<0)
		flag=1,n=-n;
		fenjie(n);
		ans=0;
		for(int i=0;i<pcnt;i++){
			ans=__gcd(ans,e[i]);
		}
		if(!flag||ans%2==1)//x是偶數或者gcd是奇數均可直接輸出
		printf("Case %d: %lld\n",cas,ans);
		else{//x是奇數
			while(ans%2==0) ans/=2;//若gcd是偶數，則需除2到是奇數為止
			printf("Case %d: %lld\n",cas,ans);
		}
	}
	return 0;
}

題意：一個很大很大的數，除以一個int型的數，問是否可整除。

思路：通過字串一位一位轉化成數字同時對要除的數取模即可。//我腦子抽了直接上java大數了

import java.util.*;//沒錯，這是java程式碼，雖然C艹寫這題也很簡單，但是我懶的再寫一遍了
import java.math.*;

public class Main
{
	public static void main(String[] args)
	{
		Scanner input = new Scanner(System.in);
		int t=input.nextInt();
		for(int cas=1;cas<=t;cas++){
			BigInteger a=input.nextBigInteger();
			BigInteger b=input.nextBigInteger();
			if(b.compareTo(BigInteger.valueOf(0))<0){ 
				b=b.multiply(BigInteger.valueOf(-1));
				a.multiply(BigInteger.valueOf(-1));
			}
			int ans=a.mod(b).intValue();
			if(ans==0){
			    System.out.println("Case "+cas+": divisible");
			}
			else
				System.out.println("Case "+cas+": not divisible");
		}
	}
}

題意挺好懂，但是還挺難描述的，就不多說了。

這種題一看就是找計算式的，大致一推規律，就可以發現公式sigma(Ai)*k*n^(k-1)%mod，k比較大，上快速冪。

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define For(i,a,b) for(int i=a;i<=b;i++)
#define INF 0x3f3f3f3f
#define N 1005
#define db double
int n,k,mod,t,ans,s;
template<class T>
inline bool scan_d(T &ret){
	char c;
	int sgn;
	if(c=getchar(),c==EOF) return 0;
	while(c!='-'&&(c<'0'||c>'9')) c=getchar();
	sgn=(c=='-')?-1:1;
	ret=(c=='-')?0:(c-'0');
	while(c=getchar(),c>='0'&&c<='9') ret=ret*10+c-'0';
	ret*=sgn;
	return 1;
}
int qpow(int a,int b){
	int res=1;
	a%=mod;
	while(b){
		if(b&1) res=(res*a)%mod;
		b>>=1;
		a=a*a%mod;
	}
	return res;
}
int main(){
	scan_d(t);
	For(cas,1,t){
		s=0;
		scan_d(n),scan_d(k),scan_d(mod);
		For(i,1,n){
			scan_d(ans);
			ans%=mod;
			s=(s+ans)%mod;
		}
		printf("Case %d: %d\n",cas,qpow(n,k-1)*(k%mod)%mod*s%mod);
	}
	return 0;
}

題意：求a到b區間內素數的個數。

思路：區間素數篩。先預處理素數篩打出素數表，注意必須包括所有可能的sqrt(b)，然後通過1到sqrt(b)區間的素數篩去a到b區間的非素數，再遍歷陣列對素數進行計數。（因為a、b數值太大，陣列開不下，需要整體偏移a，即0到b-1)

#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
using namespace std;
#define N 100005
#define ll long long
int t,a,b,prime[10005],cnt,ans;
bool noprime[N],notprime[N];
void init(){
	notprime[1]=1;
	for(int i=2;i<N;i++){
		if(!notprime[i]) prime[cnt++]=i;
		for(int j=0;j<cnt&&prime[j]*i<N;j++){
			notprime[prime[j]*i]=1;
			if(i%prime[j]==0)
			break;
		}
	}
}
int main(){
	init();
	cin>>t;
	for(int cas=1;cas<=t;cas++){
		cin>>a>>b;
		ans=0;
		memset(noprime,false,sizeof(noprime));
		int qaq=sqrt(b);
		for(int i=0;i<cnt&&prime[i]<=qaq;i++){
			ll tt=max(2ll,(a-1ll+prime[i])/prime[i]);
			for(ll j=tt;prime[i]*j<=b;j++){
				noprime[prime[i]*j-a]=true;
			}
		}
		for(int i=0;i<=b-a;i++){
			if(!noprime[i])
			ans++;
		}
		if(a==1)
		ans--;
		printf("Case %d: %d\n",cas,ans);
	}
	return 0;
}

這題xdoj上有類似的xdoj1019 自然數的祕密，我也恰好寫過部落格點我點我，也就不再多提了。思路就是二分，需要注意無解時會死迴圈，要想辦法判斷一下。

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define For(i,a,b) for(int i=a;i<=b;i++)
#define INF 0x3f3f3f3f
#define N 1005
#define db double
int n,l,r,mid,t,ans,now,f[20],num,cnt;
template<class T>
inline bool scan_d(T &ret){
	char c;
	int sgn;
	if(c=getchar(),c==EOF) return 0;
	while(c!='-'&&(c<'0'||c>'9')) c=getchar();
	sgn=(c=='-')?-1:1;
	ret=(c=='-')?0:(c-'0');
	while(c=getchar(),c>='0'&&c<='9') ret=ret*10+c-'0';
	ret*=sgn;
	return 1;
}
void init(){
	f[0]=1;
	for(int i=1;f[i-1]<=1e8;i++){
		f[i]=f[i-1]*5;
		cnt=i;
	}
}
int NOF(int x){//num of five
	int s=0;
	for(int i=1;i<=cnt;i++){
		if(f[i]<=x)
		s+=x/f[i];
	}
	return s;
}
int main(){
	init();
	scan_d(t);
	For(cas,1,t){
		scan_d(n);
		l=5,r=5*n,now=-1,num=0;
		while(l<=r){
			mid=(l+r)>>1;
			num=NOF(mid);
			if(num==n){
				now=mid;
				r=mid-1;
			}
			else if(l==r){
				break;
			}
			if(num<n){
				l=mid+1;
			}
			else
			r=mid-1;
		}
		printf("Case %d: ",cas);
		if(now==-1){
			cout<<"impossible\n";
		}
		else
		cout<<now<<"\n";
	}
	return 0;
}

這道題在這套題裡過的人數不算少。。。但可能這題的想法恰好是我想不到的，覺得比其他一些過的人少點的還難，挺好的一道題。

題意：轉化一下，可以理解為對於給定的n，求x從1到n的G[x]的和，其中G[x]定義為gcd(x,i)（i從1到x-1)的和。

首先，這題與尤拉函式有關。考慮當gcd(n,i)=j時，則有gcd(n/j,i/j)=1，所以gcd(n,i)=j的個數就是gcd(n/j,i/j)=1的個數，而gcd(n/j,i/j)=1的個數自然就是phi[n/j]。

因此一個樸素的想法是打出尤拉函式表，然後打出G[n]表，再求一個字首和，最後O(1)查詢即可。

令G[n]為n對應的所有gcd(n,i)(1<=i<n)的，G[n]打表時如果根號n列舉每個n的所有因子，然後求出G[n]的值，O(nsqrt(n))，n=4e6，這樣顯然是會超時的。。。所以我們需要列舉所有可能的因子的值i，然後內層迴圈列舉該因子的倍數n，G[n]+=i*phi[n/i]。打出G[n]的表後再求出字首和即可。

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define For(i,a,b) for(int i=a;i<=b;i++)
#define INF 0x3f3f3f3f
#define N 4000000
#define db double
ll gcd[N+5],phi[N+5];
int n;
template<class T>
inline bool scan_d(T &ret){
	char c;
	int sgn;
	if(c=getchar(),c==EOF) return 0;
	while(c!='-'&&(c<'0'||c>'9')) c=getchar();
	sgn=(c=='-')?-1:1;
	ret=(c=='-')?0:(c-'0');
	while(c=getchar(),c>='0'&&c<='9') ret=ret*10+c-'0';
	ret*=sgn;
	return 1;
}
void init(){
	For(i,1,N) phi[i]=i;
	for(int i=2;i<=N;i+=2) phi[i]/=2;
	for(int i=3;i<=N;i+=2){
		if(phi[i]==i){
			for(int j=i;j<=N;j+=i)
			phi[j]=phi[j]/i*(i-1);
		}
	} 
}
void init1(){
	For(i,1,(N+1)/2){
		for(int j=2*i;j<=N;j+=i){
			gcd[j]+=i*phi[j/i];
		}
	} 
	For(i,3,N){
		gcd[i]+=gcd[i-1];
	}
}
int main(){
	init();
	init1();
	while(scan_d(n),n){
		cout<<gcd[n]<<"\n";
	}
	
	return 0;
}

沒看題。。。以後再說

同P

題意：給定u，v，m，n，L，求(m-n)*x=v-u (%L)，即求(m-n)*x-L*y=v-u。這裡我們可以通過擴充套件歐幾里得解同餘方程。

但是我第一次寫的因為取模的問題寫出了一個bug（居然也AC了），當然後來發現了。。。

第一遍寫的：

#include<iostream>
#include<algorithm>
#include<cstdlib>
#include<cstdio>
using namespace std;
#define ll long long
#define For(i,a,b) for(int i=a;i<=b;i++)
#define INF 0x3f3f3f3f
#define N 1005
#define db double
ll n,m,x0,y0,L,ans,gc;
template<class T>
inline bool scan_d(T &ret){
	char c;
	int sgn;
	if(c=getchar(),c==EOF) return 0;
	while(c!='-'&&(c<'0'||c>'9')) c=getchar();
	sgn=(c=='-')?-1:1;
	ret=(c=='-')?0:(c-'0');
	while(c=getchar(),c>='0'&&c<='9') ret=ret*10+c-'0';
	ret*=sgn;
	return 1;
}
ll exgcd(ll a,ll b,ll &x,ll &y){
	if(b==0){
		x=1,y=0;return a;
	}
	ll d=exgcd(b,a%b,x,y);
	int t=x;x=y,y=t-a/b*y;
	return d;
}
ll solve(ll a,ll b,ll n,ll gc){
	ll x,y,k=b/gc;
	exgcd(a,n,x,y);
	return (k*x%(L/gc)+L/gc)%(L/gc);//這個地方有點小問題，13 645 31 23 1000會輸出-46而不是79
}
int main(){
	cin>>x0>>y0>>m>>n>>L;
	L=-L;
	if(m==n||(y0-x0)%(gc=__gcd(m-n,L)))
	cout<<"Impossible\n",exit(0);
	ans=solve(m-n,y0-x0,L,gc);
	cout<<ans<<endl;
	return 0;
}

第二遍取模時進行了處理，當L/gc為負數時，為保證結果是正數，需要加應該是-L/gc。

#include<iostream>
#include<algorithm>
#include<cstdlib>
#include<cstdio>
using namespace std;
#define ll long long
#define For(i,a,b) for(int i=a;i<=b;i++)
#define INF 0x3f3f3f3f
#define N 1005
#define db double
ll n,m,x0,y0,L,ans,gc;
template<class T>
inline bool scan_d(T &ret){
	char c;
	int sgn;
	if(c=getchar(),c==EOF) return 0;
	while(c!='-'&&(c<'0'||c>'9')) c=getchar();
	sgn=(c=='-')?-1:1;
	ret=(c=='-')?0:(c-'0');
	while(c=getchar(),c>='0'&&c<='9') ret=ret*10+c-'0';
	ret*=sgn;
	return 1;
}
ll exgcd(ll a,ll b,ll &x,ll &y){
	if(b==0){
		x=1,y=0;return a;
	}
	ll d=exgcd(b,a%b,x,y);
	int t=x;x=y,y=t-a/b*y;
	return d;
}
ll solve(ll a,ll b,ll n,ll gc){
	ll x,y,k=b/gc;
	exgcd(a,n,x,y);
	if(L/gc>0)
	return (k*x%(L/gc)+(L/gc))%(L/gc);
	else
	return ((k*x)%(L/gc)+(-L/gc))%(L/gc);
}
int main(){
	cin>>x0>>y0>>m>>n>>L;
	L=-L;
	if(m==n||(y0-x0)%(gc=__gcd(m-n,L)))
	cout<<"Impossible\n",exit(0);
	ans=solve(m-n,y0-x0,L,gc);
	cout<<ans<<endl;
	return 0;
}

題意：已知A，B，C，k，解C*x=B-A (% 2^k)同餘方程。

和前一題青蛙的約會有點類似，因此可以擴充套件歐幾里得來求解。

#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
#define ll long long
#define For(i,a,b) for(int i=a;i<=b;i++)
ll f[40],a,b,c,gc,t,ans;
int k;
void init(){//預先存的負值，方便之後使用
	f[0]=-1;
	For(i,1,32){
		f[i]=f[i-1]*2;
	}
}
void exgcd(ll a,ll b,ll &x,ll &y){
	if(b==0) x=1,y=0;
	else
	exgcd(b,a%b,x,y),t=x,x=y,y=t-a/b*y;
}
ll solve(ll a,ll b,ll c){
	ll x,y,k=c/gc,tt1=b/gc,tt=b/gc;
	exgcd(a,b,x,y);
	if(tt<0)
	tt1=-tt;
	return (k*x%tt+tt1)%tt;
}
int main(){
	init();
	while(cin>>a>>b>>c>>k,a||b||c||k){
		//c*x=b-a(%2^k) c*x-f[k]*y=b-a
		gc=__gcd(c,f[k]);
		if((b-a)%gc!=0){
			cout<<"FOREVER\n";
		}
		else{
			ans=solve(c,f[k],b-a);
			cout<<ans<<endl;
		}
	}
	return 0;
} 

題意：用斐波那契數列表示數x，若x=f[2]+f[0]，則x可以表示為101。用沒有相鄰的1的斐波那契表示法表示數x和y，並對它們的和同樣用沒有相鄰的1的斐波那契表示法表示。

這題算是貪心？可以想到一個結論，假設某個數從它所能包含的最大的斐波那契數開始表示，那麼一定沒有相鄰的1。為什麼呢？假設該數的某個表示含有兩個相鄰的1——即f[j]和f[j-1]，那麼這兩位一定可以用f[j+1]來表示，我們的貪心使其變為了1位；若有f[j]、f[j-1]、f[j-2]，則顯然會變為f[j+1]、f[j-2]，不再相鄰。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
#define ll long long
#define For(i,a,b) for(int i=a;i<=b;i++)
#define INF 0x3f3f3f3f
#define N 105
#define db double
ll f[N],tt;
char ac[N],bc[N];
void init(){
	f[0]=1,f[1]=2;
	For(i,2,40) f[i]=f[i-1]+f[i-2];
}
struct node{
	char cnum[N];
	ll num,ws;
	int kg;
}a,b,c;
void cal(node &aa){
	aa.ws=strlen(aa.cnum)-1,aa.num=0;
	for(int i=aa.ws;i>=0;i--){
		aa.num+=(aa.cnum[i]-'0')*f[aa.ws-i];
	}
}
void incal(node &aa){
	tt=aa.num,aa.ws=-1;
	for(int i=40;i>=0;i--){
		if(tt>=f[i]){
			tt-=f[i],aa.cnum[++aa.ws]='1';
		}
		else if(aa.ws>=0||i==0)
		aa.cnum[++aa.ws]='0';
	}
	aa.cnum[aa.ws+1]='\0';
}
void print(node aa){
	For(i,1,aa.kg) cout<<" ";
	cout<<aa.cnum<<"\n";
}
int main(){
	init();
	while(cin>>a.cnum>>b.cnum){//按fib數列由大至小分解出來的1一定兩兩不相鄰
		//因為若某個數分解後出現倆個相鄰的1，則這兩位加起來可以由更大的一位表示！
		cal(a),cal(b),c.num=a.num+b.num;
		incal(c),incal(a),incal(b);
		c.kg=2,a.kg=c.ws-a.ws+2,b.kg=c.ws-b.ws+1;
		print(a),cout<<"+",print(b);
		For(i,1,c.kg) cout<<" ";
		For(i,1,c.ws+1) cout<<"-";
		cout<<"\n";
		print(c);
		cout<<"\n";
	} 
	return 0;
}

題意：判斷一個數是不是素數。數範圍很小，個數也不多，根號n的複雜度暴力判斷或者預處理素數篩都行。

#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;
int n;
bool f(int t){
	if(t==1||t==2)
	return false;
	for(int i=2;i<=sqrt(t);i++){
		if(t%i==0)
		return false;
	}
	return true;
}
int main(){
	int d=1;
	while(scanf("%d",&n)){
		if(n<=0)
		break;
		if(f(n)){
			cout<<d<<": yes\n";
		}
		else
		cout<<d<<": no\n";
		d++;
	}
	return 0;
}

題意：對給定的一堆數字求兩兩之間最大的gcd值。

不得不說，這輸入真是毒瘤。。。因為不清楚每組資料究竟有多少個數，先以字串形式讀入一行，再處理成對應的數。

因為資料量不大，直接兩兩求gcdO(n^2)暴力即可。

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
int a[110];
int gcd(int l,int b){
	return b==0?l:gcd(b,l%b);
}
int main(){
	int n;
	char c;
	cin>>n;
	getchar();
	while(n--){
		memset(a,0,sizeof(a));
		int num=0,flag=0;
		while(scanf("%c",&c)){
			if(c=='\n'){
				if(flag==0)
				num++;
				break;
			}	
			if(c>='0'&&c<='9'){
				a[num]=a[num]*10+c-'0';
				flag=0;
			}
			else if(c==' '&&flag==0){
				flag=1;
				num++;
			}
		}
		int ans=0;
		for(int i=0;i<num-1;i++){
			for(int j=i+1;j<num;j++){
				ans=max(ans,gcd(a[i],a[j]));
			}
		}
		cout<<ans<<endl;
	}
	return 0;
}

題意：求[a,b]區間內i*i+i+41為素數所佔的比例，保留兩位小數。

方法很簡單，因為資料量不大，直接預處理出素數個數的字首和，然後算一下就好。然而！！！這裡一個大問題，精度。。。求dalao告知為啥最後要加點東西才能過。。。

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define For(i,a,b) for(int i=a;i<=b;i++)
#define INF 0x3f3f3f3f
#define N 1005
#define db double
int a,b,tt,tat,ans;
template<class T>
inline bool scan_d(T &ret){
	char c;
	int sgn;
	if(c=getchar(),c==EOF) return 0;
	while(c!='-'&&(c<'0'||c>'9')) c=getchar();
	sgn=(c=='-')?-1:1;
	ret=(c=='-')?0:(c-'0');
	while(c=getchar(),c>='0'&&c<='9') ret=ret*10+c-'0';
	ret*=sgn;
	return 1;
}
bool flag;
int sum[10005];
void init(){
	sum[0]=1;
	For(i,1,10000){
		if(i<40){
			sum[i]=sum[i-1]+1;
			continue;
		}
		tt=i*i+i+41,tat=sqrt(tt),flag=1;
		For(j,2,tat){
			if(tt%j==0){
				flag=0;
				break;
			}
		}
		sum[i]=sum[i-1]+flag;
	}
}
int main(){
	init();
	while(cin>>a>>b){
		db fz=sum[b]-(a==0?0:sum[a-1]),fm=(b-a+1);
		printf("%.2lf\n",fz/fm*100+1e-5);//+1e-5,1e-6,1e-8,1e-10,1e-12都行，1e-4不行，其他沒試
	}
	return 0;
}

題意：求法裡數列的個數。法裡數列定義啥的看原題。

很容易想到，第n項新增的法裡數列的個數是與n互質的數的個數，也就是尤拉函式phi[n]，預處理字首和即可。

#include<iostream>
#include<cstdio>
using namespace std;
#define ll long long
#define For(i,a,b) for(int i=a;i<=b;i++)
#define INF 0x3f3f3f3f
#define N 1000000
#define db double
int n,m,t,ans,phi[N+5];
ll f[N+5];
template<class T>
inline bool scan_d(T &ret){
	char c;
	int sgn;
	if(c=getchar(),c==EOF) return 0;
	while(c!='-'&&(c<'0'||c>'9')) c=getchar();
	sgn=(c=='-')?-1:1;
	ret=(c=='-')?0:(c-'0');
	while(c=getchar(),c>='0'&&c<='9') ret=ret*10+c-'0';
	ret*=sgn;
	return 1;
}
void getphi(){
	For(i,1,N) phi[i]=i;
	for(int i=2;i<=N;i+=2) phi[i]/=2;
	for(int i=3;i<=N;i+=2){
		if(phi[i]==i){
			for(int j=i;j<=N;j+=i){
				phi[j]=phi[j]/i*(i-1);
			}
		}
	} 
}
void getf(){
	f[2]=1;
	For(i,3,N){
		f[i]=f[i-1]+phi[i];
	}
}
int main(){
	getphi();
	getf();
	while(scan_d(n),n){
		cout<<f[n]<<endl;
	}
	return 0;
}

題意：按大小順序輸出1到(2^64)-1的所有"super power number"，其中"super power number"的定義是能表示成x^y和m^n，其中x>0&&m>0&&y>1&&n>1。

由算術基本定理，可以想到，將num分解質因數後，若所有冪次的gcd不為質數，則gcd至少含有兩個非1因子，即num至少可表示x^y和m^n兩種形式，其中gcd%y==0&&gcd%n==0。

上述情況即為滿足條件的數，那麼我們可以開始構造，先特判加上1，列舉底數i從2到sqrt(sqrt(2^64 -1))也就是65535——因為至少4次冪才滿足條件——迴圈內部再列舉每個底數的冪次numi和冪數j，如果numi是非質數就把j存起來，即為一個滿足條件的數，注意2^64-1恰好是unsigned long long所能表示的最大數值，因此要防止溢位。列舉完畢後再排個序即可。

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define ull unsigned long long
#define For(i,a,b) for(int i=a;i<=b;i++)
#define INF 0x3f3f3f3f
#define N 4000000
#define db double
int cnt,prime[100];
bool np[100];
void Prime(){
	np[1]=1;
	For(i,2,90){
		if(!np[i]) prime[cnt++]=i;
		for(int j=0;j<cnt&&prime[j]*i<=90;j++){
			np[prime[j]*i]=1;
			if(i%prime[j]==0) break;
		} 
	}
}
map<ull,bool> mp;
void init(){
	ull maxnum=1;
	For(i,1,63){
		maxnum*=2;
	}
	maxnum+=(maxnum-1);
	mp.insert(make_pair(1,true));
	int tt=65535;
	ull tt1,j,numi;
	For(i,2,tt){
		j=i*1ull*i*i*i,numi=4;
		while(1){
			if(numi>=4&&np[numi]) mp[j]=true;
			if(j<=maxnum/i) j*=i,numi++;//此處防止溢位，不可能等到j大於2^64-1再判斷，因此要提前一點判斷。
			else break;
		}
	}
}
int main(){
	Prime();
	init();
	map<ull,bool>::iterator it=mp.begin();
	for(;it!=mp.end();it++){
		cout<<it->first<<"\n";
	}
	return 0;
}

其餘三題估計短時間內不會補