問題背景：

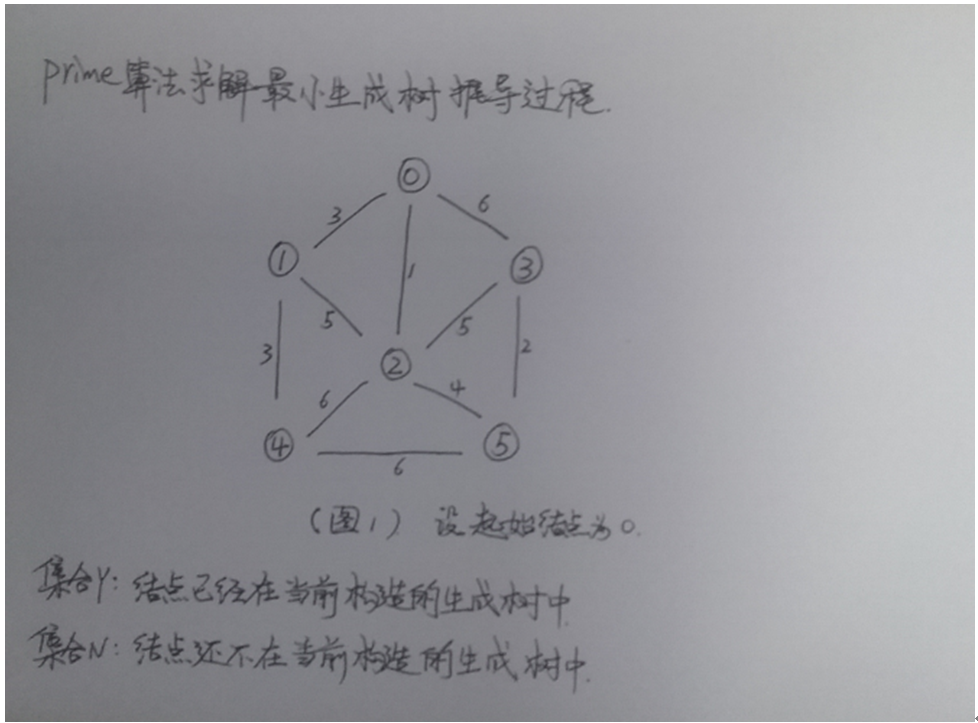
對於一個圖，它的所有生成樹中必有一個“邊的權值最小”的生成樹，我們把它稱為最小生成樹。

概念很抽象，換做實際問題：

有十個城市，各個城市之間距離或遠或近。需要建設一個道路網，把十個城市連線在一起，要求道路網的道路長度最小。

各個城市的連線可以抽象為一個圖，本質上即是求該圖的一個最小生成樹。

每一個圖可能有多個生成樹，但最小生成樹 所有邊的權值之和是最小的。

Prime演算法簡介：

最小生成樹和最短路徑一樣，都是在實際中非常常見的圖演算法問題。

同樣也有專門的演算法來構造圖的最小生成樹。

Prime演算法是求解最小生成樹問題最常用的演算法，思想和上次講解的 最短路徑Dijkstra演算法 有些接近。

1.     把所有節點分成兩類，一類是已經加入到了 當前的生成樹中（集合 Y） ，一類是還沒有加入當前的生成樹中（集合N）。

PS:  1. 顯然，這種分類可以用flag來設定。

         2. 最終的生成樹是一步一步構造的，所以說是 “當前的”生成樹。

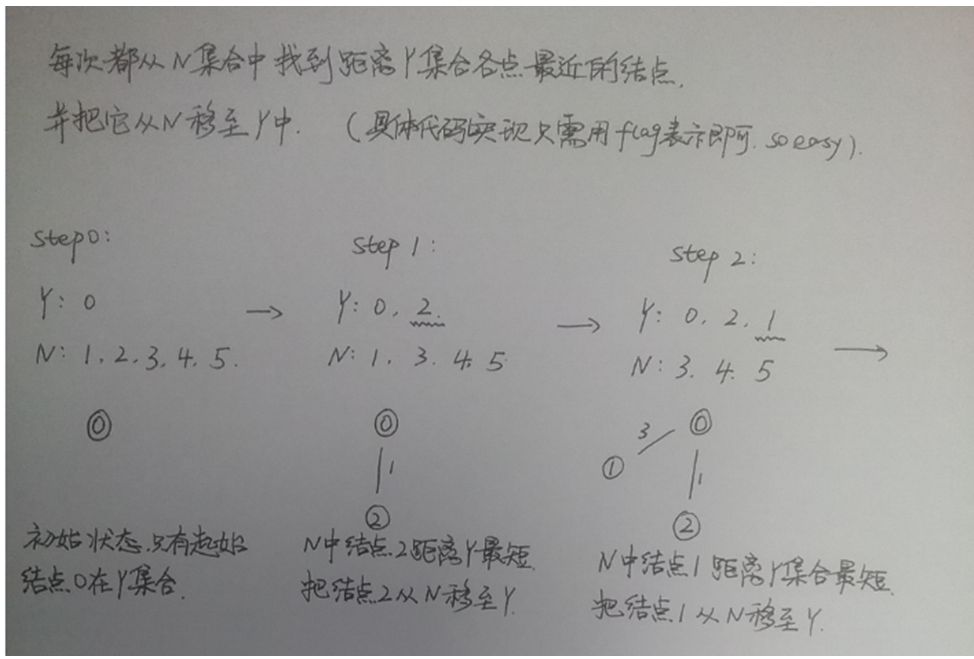
2.     從 Y 中取得一個節點 Vy, 從 N 中取得一個節點 Vn. 使其滿足 Vy和Vn之間邊的權值最小。

3、 找到滿足上述條件的節點後，把Vn結點從 N 移入 Y中。

Ps： 具體程式碼實現是，flag值修改即可。 （最原始的做法，後續會有改進方式）

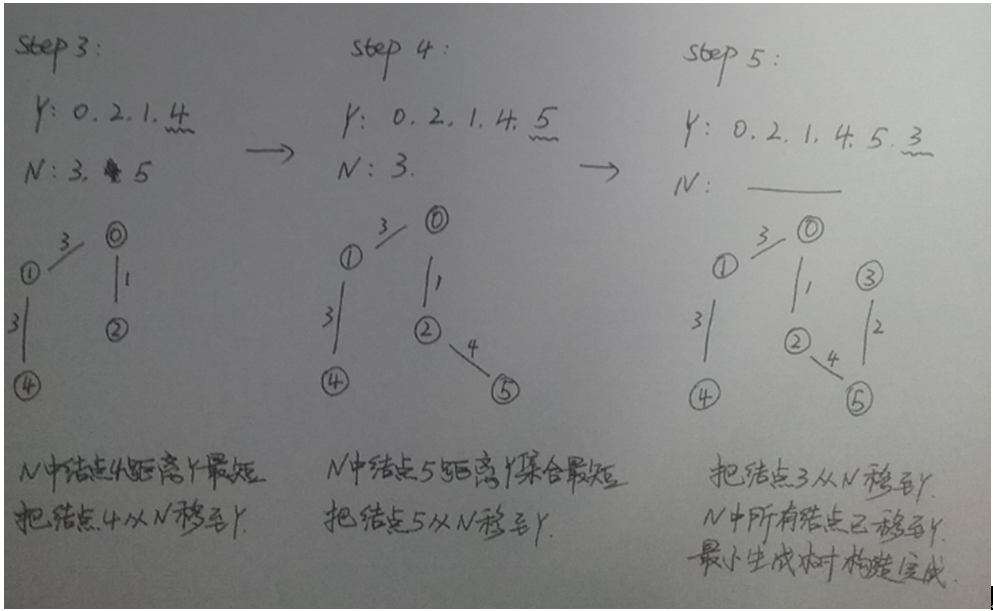
3.     重複上述 2. 3. 兩步，直到所有節點全部加入Y中。

具體例子：

程式碼轉化與具體實現：

程式碼實現時需要注意的幾個問題：

1.     如何表示集合Y 和集合 N

當然，可以使用一個flag陣列表示，比如為true表示在Y中，false在N中。

2.     集合Y和集合N中均可能有多個節點，如何從N集合中找到符合條件（距離Y中所有節點最近）的結點？

最粗暴的方法，每次都分別遍歷 Y 和 N集合，兩重遍歷可以找到N中的該結點，但是效率會很差。可以從資料結構設計的角度改善。

建立一個數組， int minDis[ N ]

對於其中元素 minDis[i]，其含義是 j 節點到 Y 集合所有節點距離的最小值。

尋找N中符合條件的結點時，只需要遍歷N集合中結點minDis的資料，找到最小值即可。

顯然，對於Y集合中的結點 i ，minDis[i]都是 0.

這樣，minDis陣列也可以替代上步中的flag陣列： minDis值是0，即代表結點在Y集合中。

3.     每次從N集合中找到符合條件的結點 i 後，都需要做哪些處理？

首先，要把它從N移動到Y中。 minDis[i] = 0 即可。（原因參考上步的說明）

其次，要判斷是否需要更新N中剩餘結點 mindDis的值。

因為minDis[j] 儲存的是j結點到Y中所有結點距離的最小值，當把i結點從N移動到Y中後，Y集合元素增多，對於N中剩餘結點j而言，minDis[j]的值可能會減小。

什麼情況下該值會減小？

當從N移動到Y中的結點 I 距離 j結點的值 小於 當前 minDis[j]的值，就需要更新minDis.

參考程式碼：

		#define N 100
		int matrix[N][N];

		//最小生成樹資訊
		int treeLenthResult = 0; 	//最終生成的最小生成樹 邊的權值之和
		int minDis[N];
		int closeVertex[N]; 
		
		//設定起始結點下標是0 （從頂點0開始構造）
		//初始化minDis
		for (int i = 0; i < N; i++) {
			minDis[i] = matrix[i][0];
			closeVertel[i] = 0;
		}
		//起始結點初始化
		minDis[0] = 0;
		closeVertel[0] = 0;

		//N-1次遍歷，每次都從集合N中找到一個結點，距離集合Y中所有結點值最小
		for (int i = 1; i < N; i++) {
			int tmpDis = INF;
			int tmpLoc = -1;
			for (int j = 0; j < N; j++) {
				//minDis[j] != 0  --> j結點不在當前的生成樹中
				if ((minDis[j] != 0) && (minDis[j] < tmpDis) ) {
					tmpDis = minDis[j];
					tmpLoc = j;
				}
			}
			
			if (tmpLoc != -1) {
				//tmpLoc結點 是本輪迴圈中找到的目標結點
				//更新當前得到生成樹邊的權值之和
				treeLenthResult += tmpDis;	
			}

			//tmpLoc結點從N結合移至Y集合
			minDis[tmpLoc] = 0;
			//更新N集合中剩餘的其他結點
			for (int j = 0; j < N; j++) {
				if (minDis[j] > matrix[j][tmpLoc]) {
					minDis[j] = matrix[j][tmpLoc];
					closeVertex[j] = tmpLoc;		//此時，j結點距離Y集合中 tmpLoc結點最近
				}
			}
		}