【[HNOI2011]數學作業】
阿新 • • 發佈:2019-01-02
我又對著跑出正解的程式調了好久
怕不是眼瞎了
這就是個分段矩陣,我們很容易就得到了遞推式
$\(f[i]=f[i-1]*10^k+i\)
其中\(k=log_{10}i\)
於是就是分段矩陣
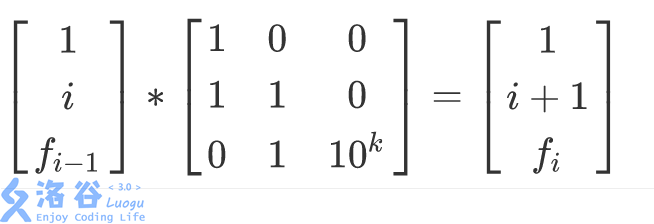
之後就是程式碼了,沒有加快速乘WA了好久
#include<iostream> #include<cstring> #include<cstdio> #define re register #define LL long long LL n,m; LL ans[4][4],a[4][4]; LL Ans=0; inline LL mul(LL a,LL b) { LL s=0; while(b) { if(b&1ll) s=s+a%m; b>>=1ll; a=a+a%m; } return s; } inline void did_a() { LL mid[4][4]; for(re int i=1;i<=3;i++) for(re int j=1;j<=3;j++) mid[i][j]=a[i][j],a[i][j]=0; for(re int i=1;i<=3;i++) for(re int j=1;j<=3;j++) for(re int p=1;p<=3;p++) a[i][j]=(a[i][j]+mul(mid[i][p],mid[p][j])%m)%m; } inline void did_ans() { LL mid[4][4]; for(re int i=1;i<=3;i++) for(re int j=1;j<=3;j++) mid[i][j]=ans[i][j],ans[i][j]=0; for(re int i=1;i<=3;i++) for(re int j=1;j<=3;j++) for(re int p=1;p<=3;p++) ans[i][j]=(ans[i][j]+mul(mid[i][p],a[p][j])%m)%m; } inline void Rebuild(LL t) { memset(a,0,sizeof(a)),memset(ans,0,sizeof(ans)); ans[1][1]=a[1][1]=1ll; ans[2][1]=a[2][1]=1ll; ans[2][2]=a[2][2]=1ll; ans[3][2]=a[3][2]=1ll; ans[3][3]=a[3][3]=t; } inline void Quick(LL b) { while(b) { if(b&1ll) did_ans(); b>>=1ll; did_a(); } } inline void work() { LL now=1; LL t=10; while(now<=n) { if(t<0) return; Rebuild(t); if(n>=t-1) Quick(t-1-now); else Quick(n-now); Ans=(ans[3][1]%m+mul(now,ans[3][2])%m+mul(Ans,ans[3][3])%m)%m; now=t; t*=10; } } int main() { scanf("%lld%lld",&n,&m); work(); printf("%lld\n",Ans); return 0; }
