實現功能：

在自編碼器（autoencoder）中有編碼器（encoder）和解碼器（decoder）。我們只看 encoder 壓縮的過程，使用它將一個數據集降維到只有兩個Feature時，將資料放入一個二維座標系內。

思路：

我們只顯示 encoder 之後的資料， 並畫在一個二維直角座標系內。做法很簡單，我們將原有 784 Features 的資料壓縮成僅剩 2 Features 的資料。

實現程式碼：

import tensorflow as tf
import matplotlib.pyplot as plt

# Import MNIST data
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("/tmp/data", one_hot= False)

# Visualize decoder setting
# Parameter
learning_rate = 0.01    # 0.01 this learning rate will be better! Tested
training_epochs = 10	# 10 Epoch 訓練
batch_size = 256
display_step = 1

# Network Parameters
n_input = 784  # MNIST data input (img shape: 28*28)

# tf Graph input(only pictures)
X = tf.placeholder("float",[None, n_input])

# hidden layer settings
n_hidden_1 = 128
n_hidden_2 = 64
n_hidden_3 = 10
n_hidden_4 = 2
weights = {
    'encoder_h1': tf.Variable(tf.truncated_normal([n_input, n_hidden_1],)),
    'encoder_h2': tf.Variable(tf.truncated_normal([n_hidden_1, n_hidden_2],)),
    'encoder_h3': tf.Variable(tf.truncated_normal([n_hidden_2, n_hidden_3],)),
    'encoder_h4': tf.Variable(tf.truncated_normal([n_hidden_3, n_hidden_4],)),

    'decoder_h1': tf.Variable(tf.truncated_normal([n_hidden_4, n_hidden_3],)),
    'decoder_h2': tf.Variable(tf.truncated_normal([n_hidden_3, n_hidden_2],)),
    'decoder_h3': tf.Variable(tf.truncated_normal([n_hidden_2, n_hidden_1],)),
    'decoder_h4': tf.Variable(tf.truncated_normal([n_hidden_1, n_input],)),
	}
biases = {
    'encoder_b1': tf.Variable(tf.random_normal([n_hidden_1])),
    'encoder_b2': tf.Variable(tf.random_normal([n_hidden_2])),
    'encoder_b3': tf.Variable(tf.random_normal([n_hidden_3])),
    'encoder_b4': tf.Variable(tf.random_normal([n_hidden_4])),

    'decoder_b1': tf.Variable(tf.random_normal([n_hidden_3])),
    'decoder_b2': tf.Variable(tf.random_normal([n_hidden_2])),
    'decoder_b3': tf.Variable(tf.random_normal([n_hidden_1])),
    'decoder_b4': tf.Variable(tf.random_normal([n_input])),
	}

# Building the encoder
def encoder(x):
    layer_1 = tf.nn.sigmoid(tf.add(tf.matmul(x, weights['encoder_h1']),
                                   biases['encoder_b1']))
    layer_2 = tf.nn.sigmoid(tf.add(tf.matmul(layer_1, weights['encoder_h2']),
                                   biases['encoder_b2']))
    layer_3 = tf.nn.sigmoid(tf.add(tf.matmul(layer_2, weights['encoder_h3']),
                                   biases['encoder_b3']))
    layer_4 = tf.add(tf.matmul(layer_3, weights['encoder_h4']),
                                    biases['encoder_b4'])
    return layer_4

# Building the decoder
def decoder(x):
    layer_1 = tf.nn.sigmoid(tf.add(tf.matmul(x, weights['decoder_h1']),
                                   biases['decoder_b1']))
    layer_2 = tf.nn.sigmoid(tf.add(tf.matmul(layer_1, weights['decoder_h2']),
                                   biases['decoder_b2']))
    layer_3 = tf.nn.sigmoid(tf.add(tf.matmul(layer_2, weights['decoder_h3']),
                                biases['decoder_b3']))
    layer_4 = tf.nn.sigmoid(tf.add(tf.matmul(layer_3, weights['decoder_h4']),
                                biases['decoder_b4']))
    return layer_4

# Construct model
encoder_op = encoder(X) 			# 128 Features
decoder_op = decoder(encoder_op)	# 784 Features

# Prediction
y_pred = decoder_op	# After
# Targets (Labels) are the input data.
y_true = X			# Before

# Define loss and optimizer, minimize the squared error
cost = tf.reduce_mean(tf.pow(y_true - y_pred, 2))
optimizer = tf.train.AdamOptimizer(learning_rate).minimize(cost)

# Launch the graph
with tf.Session() as sess:
    # tf 馬上就要廢棄tf.initialize_all_variables()這種寫法
    # 替換成下面:
    sess.run(tf.global_variables_initializer())
    total_batch = int(mnist.train.num_examples/batch_size)
    # Training cycle
    for epoch in range(training_epochs):
        # Loop over all batches
        for i in range(total_batch):
            batch_xs, batch_ys = mnist.train.next_batch(batch_size)  # max(x) = 1, min(x) = 0
            # Run optimization op (backprop) and cost op (to get loss value)
            _, c = sess.run([optimizer, cost], feed_dict={X: batch_xs})
        # Display logs per epoch step
        if epoch % display_step == 0:
            print("Epoch:", '%04d' % (epoch+1),
                  "cost=", "{:.9f}".format(c))

    print("Optimization Finished!")

    encoder_result = sess.run(encoder_op, feed_dict={X: mnist.test.images})
    plt.scatter(encoder_result[:, 0], encoder_result[:, 1], c=mnist.test.labels)
    plt.show()
 

實現結果：

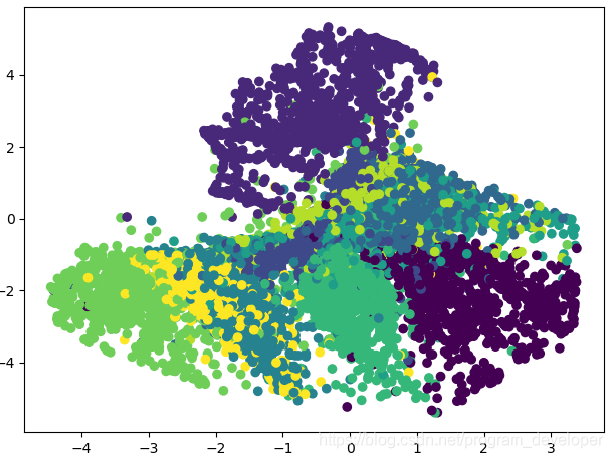
 實驗結果分析：

我們知道mnist資料集中有10個數字，也就是有10類資料，每個數字是以28*28（784）維圖片展示的。我們在上面的實驗中將所有資料降維到2維資料，並展示在二維資料座標中。從圖1中我們可以看到，所有資料降到2維之後，還是可以把相同類別的資料歸到同一類中。在圖1中，同樣顏色的點，代表分到同一類的資料（Lebel相同）。在這個實驗中自編碼器（autoencoder）類似於PCA，起到了降維的作用。

Reference：