梯度下降

學習完基礎知識和矩陣運算之後，我們再回頭看下第一節講的線性迴歸的程式碼：

import tensorflow as tf
import numpy as np

trX = np.linspace(-1, 1, 101)
trY = 2 * trX + np.random.randn(*trX.shape) * 0.33 # 建立一些線性值附近的隨機值

X = tf.placeholder("float") 
Y = tf.placeholder("float")

def model(X, w):
    return tf.multiply(X, w) # X*w線性求值，非常簡單

w = tf.Variable(0.0, name="weights") 
y_model = model(X, w)

cost = tf.square(Y - y_model) # 用平方誤差做為優化目標

train_op = tf.train.GradientDescentOptimizer(0.01).minimize(cost) # 梯度下降優化

# 開始建立Session幹活！
with tf.Session() as sess:
    # 首先需要初始化全域性變數，這是Tensorflow的要求
    tf.global_variables_initializer().run()

    for i in range(100):
        for (x, y) in zip(trX, trY):
            sess.run(train_op, feed_dict={X: x, Y: y})

    print(sess.run(w)) 
 

除了這一句

train_op = tf.train.GradientDescentOptimizer(0.01).minimize(cost)

應該都可以看懂了。
我們這一節就來講看不懂的這一行，梯度下降優化函式。

從畫函式圖形說起

所謂梯度下降，其實沒有什麼神祕的，就是求個函式極值問題而己。
函式比矩陣強的一點是可以畫圖啊。

所以我們先學習一下如何畫函式的圖形：

import matplotlib.pyplot as plt
import numpy as np

x = np.linspace(-10,10,1000)
y = x ** 2 - 2 * x+ 1
plt.plot(x, y)
plt.title("matplotlib")
plt.xlabel("height")
plt.ylabel("width")
# 設定圖例
plt.legend(["X","Y"], loc="upper right")
plt.grid(True)
plt.show()
 

上面我們用np.linspace來生成若干點組成的向量，然後取y=x2−2x+1y=x2−2x+1的值。
畫出的影象是這樣的：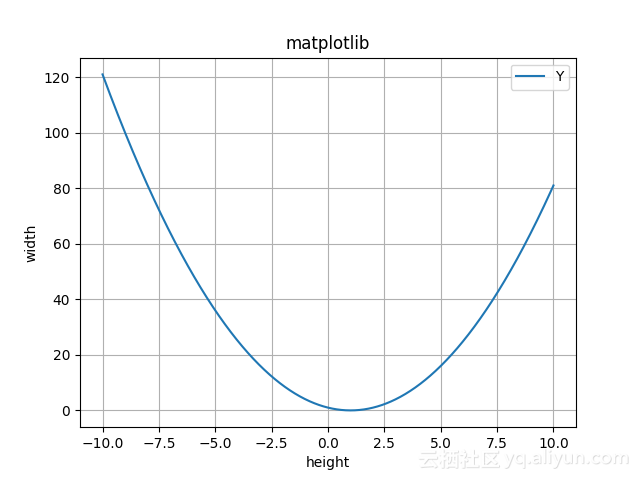

求函式的最小值

現在我們想要求這條曲線上的最小值點。因為這個函式的定義域是無限的，我們不可能從負無窮到正無窮挨個試那個最小。
但是，我們可以隨便找一個點為起點，然後比較一下它左邊相鄰一點的點和右邊和它相鄰一點的點看看哪個更小。然後取較小的那個點，繼續這個過程。

假設我們從x=-5這個座標開始，y=(-5)(-5)-2(-5)+1=36。所以這個點是(-5,36). 
我們取0.1為步長，看看-5.1和-4.9的y值是多少，發現同(-5.1, 37.21)和(-4.9,34.81)。-4.9的值更小，於是-4.9就成為新一輪迭代的值。然後從(-4.9,34.81)到(-4.8,33.64)，以此類推。一直到(1.0, 0)達到最小值，左右都比它大，這個極值就找到了。
求極值的這個函式我們稱為損失函式loss function，或代價函式cost function，或者誤差函式error function。這幾個名稱可以互換使用。
求得的極小值，我們稱為x∗=argminf(x)x∗=argminf(x)

這種方法可以解決問題。但是它的問題在於慢。在函式下降速度很快的時候可以多移動一點加快速度，下降速度變慢了之後少移一點防止跑過了。

那麼這個下降速度如何度量呢？我們都學過，用導數-derivative，也就是切線的斜率。有了導數之後，我們可以沿著導數的反方向，也就是切換下降的方向去尋找即可。
這種沿著x的導數的反方向移動一小步來減少f(x)值的技術，就被稱為梯度下降 - gradient descent.
第n+1的值為第n次的值減去導數乘以一個可以調整的係數。
也就是
xn+1=xn−ηdf(x)dxxn+1=xn−ηdf(x)dx
其中，這個可調整的係數ηη，我們稱為學習率。學習率越大下降速度越快，但是也可能錯過最小值而產生振盪。
選擇學習率的方法一般是取一個小的常數。也可以通過計算導數消失的步長。還可以多取幾個學習率值，然後取效果最好的一個。

f(x)=x2−2x+1f(x)=x2−2x+1的導函式為f′(x)=2x−2f′(x)=2x−2
我們還是選擇從(-5,36)這個點為起點，學習率我們取0.1。
則下一個點$x_2=-5 - 0.1 （2（-5）-2）= -3.8$
則第2個點下降到(-3.8,23.04)。比起第一種演算法我們右移0.1，這次一下子就右移了1.2,效率提升12倍。

晉階三維世界

我們看下我們在做線性迴歸時使用的損失函式：

cost = tf.square(Y - y_model)

這是個平方函式fLoss=Σni=1(yi−(wxi+b))2fLoss=Σi=1n(yi−(wxi+b))2
其中yiyi是已知的標註好的結果，xixi是已知的輸入值。未知數只有兩個，w和b。
所以下一步求梯度下降的問題變成求二元二次函式極小值的問題。

我們還是先看圖，二元二次函式的圖是什麼樣子的。我們取個f(x,y)=x2+y2+x+y+1f(x,y)=x2+y2+x+y+1為例吧。

先學畫圖：

from mpl_toolkits.mplot3d import Axes3D
import numpy as np
import matplotlib.pyplot as plt

# 建立 3D 圖形物件
fig = plt.figure()
ax = Axes3D(fig)

X3 = np.linspace(-10,10,100)
Y3 = np.linspace(-10,10,100)
X3, Y3 = np.meshgrid(X3, Y3)
Z3 = X3*X3 + Y3*Y3 + X3 + Y3 + 1
ax.plot_surface(X3, Y3, Z3, cmap=plt.cm.winter)

# 顯示圖
plt.show()

圖繪製出來是這樣子的：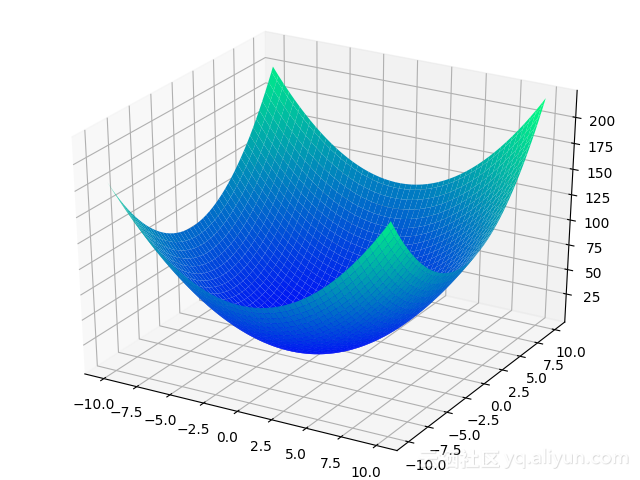

從一條曲線變成了一個碗一樣的曲面。但是仍然是有最小值點的。

現在不只是有x一個方向，而是有x和y兩個方向。兩個方向也好辦，x方向和y方向分別找梯度就是了。分別取x和y方向的偏微分。
xn+1=xn−η∂f(x,y)∂x,yn+1=yn−η∂f(x,y)∂yxn+1=xn−η∂f(x,y)∂x,yn+1=yn−η∂f(x,y)∂y

偏導數雖然從dd換成了∂∂，但是求微分的公式還是一樣的。只不過在求x的時候把y當成常數就是了。

我們可以用梯度符號來簡單表示∇=(∂f(x,y)∂x,∂f(x,y)∂y)∇=(∂f(x,y)∂x,∂f(x,y)∂y)，這個倒三角符號讀作nabla.

在Tensorflow裡，梯度下降這樣基本的操作自然是不需要我們操心的，我們只需要呼叫tf.train.GradientDescentOptimizer就好。

例子我們在前面已經看過了，我們複習一下：

cost = tf.square(Y - y_model) # 用平方誤差做為優化目標

train_op = tf.train.GradientDescentOptimizer(0.01).minimize(cost) # 梯度下降優化

賦給GradientDescentOptimizer的0.01就是我們的ηη，學習率。

自適應梯度演化史

如果您的邏輯思維比較強的話，一定會發現從二維導數升級到三維梯度時，有一個引數我們沒有跟著一起擴容，那就是學習率ηη.

我們還是看一個圖，將上面的方程變成f(x,y)=8x2+y2+x+y+1f(x,y)=8x2+y2+x+y+1

Z3 = 8*X3*X3 + Y3*Y3 + X3 + Y3 + 1

影象變成下面這樣子：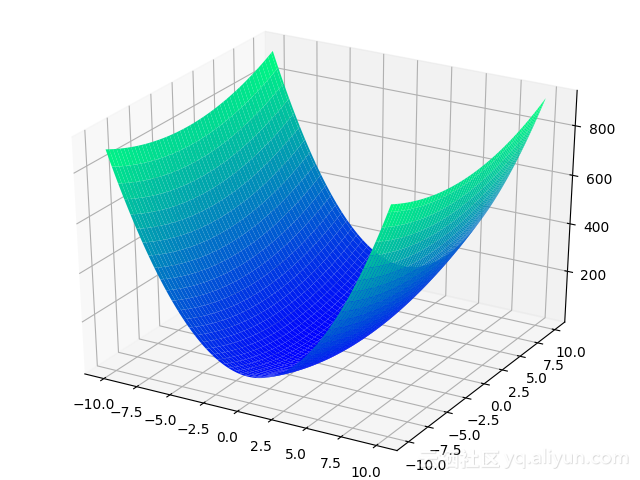

大家可以直觀地感受到，∂f(x,y)∂x∂f(x,y)∂x和∂f(x,y)∂y∂f(x,y)∂y方向的下降速度是明顯不一樣的。
如果對於更高維的情況，問題可能更嚴重，眾口難調。

最簡單的方法可能是對於每個維度都用一個專門的學習率。不過這樣也太麻煩了，這時Adaptive Gradient自適應梯度下降就被當時在UC伯克利讀博士的John C. Duchi提出了，簡寫為AdaGrad. 
在Tensorflow中，我們可以通過tf.train.AdagradOptimizer來使用AdaGrad.

AdaGrad的公式為(xt+1)i=(xt)i−ηΣtτ=1(∇f(xτ))2i√(∇f(xt))i(xt+1)i=(xt)i−ηΣτ=1t(∇f(xτ))i2(∇f(xt))i

但是，AdaGrad也有自己的問題。雖然初始指定一個ηη值之後可以自適應，但是如果這個ηη太大的話仍然會導致優化不穩定。但是如果太小了，隨著優化，這個學習率會越來越小，可能就到不了極小值就停下來了。

於是當時在Google做實習生的Mathew Zeiler做出了兩點改進：一是引入時間視窗概念，二是不用手動指定學習率。改進之後的演算法叫做AdaDelta. 
公式中用到的RMS是指Root Mean Square，均方根. 
AdaDelta的公式為(∇xi)i=−(RMS[Δx]t−1)i(RMS[g]t)i(∇f(xi))i(∇xi)i=−(RMS[Δx]t−1)i(RMS[g]t)i(∇f(xi))i
具體過程請看Zeiler同學寫的paper: http://arxiv.org/pdf/1212.5701v1.pdf

在Tensorflow中，我們只要使用tf.train.AdadeltaOptimizer這個封裝就好。

AdaDelta並不是唯一的改進方案，類似的方案還有RMSProp, Adam等。我們可以使用tf.train.RMSPropOptimizer和tf.train.AdamOptimizer來呼叫就好了。

還記得第1節中我們講卷積神經網路的例子嗎？我們用的不再是梯度下降，而是RMSProp：

cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits=py_x, labels=Y))
train_op = tf.train.RMSPropOptimizer(0.001, 0.9).minimize(cost)
predict_op = tf.argmax(py_x, 1)

物理學的啟示

雖然各種自適應梯度下降方法洋洋大觀，但是複雜的未必就是最好的。導數的物理意義可以認為是速度。速度的變化我們可以參考物理學的動量的概念，同時引入慣性的概念。如果遇到坑，靠動量比較容易衝出去，而其它方法就要迭代很久。
在Tensorflow中，可以通過tf.train.MomentumOptimizer來使用動量方法。

我們可以看一下Mathew Zeiler的論文中對於幾種方法的對比：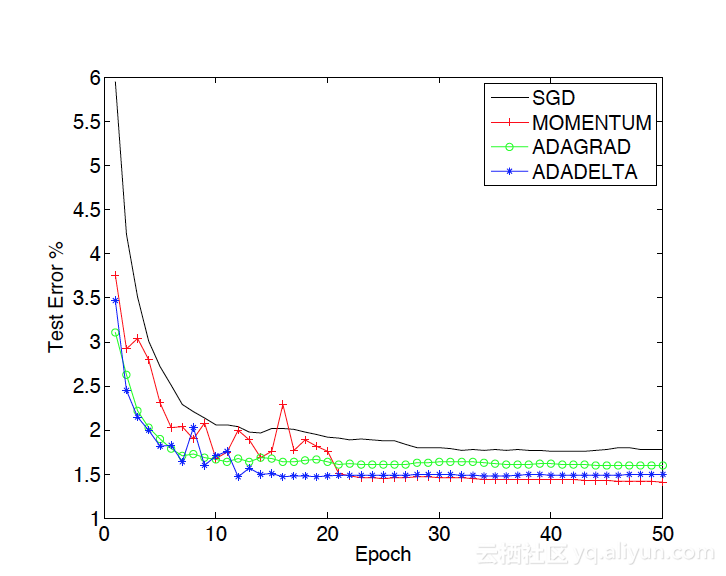

從中可以看到，雖然在前期，動量方法上竄下跳不像AdaGrad穩定，但是後期效果仍然是最好的。