在逆序對的問題中，如果採用暴力求解的方法，一般也是有效的，但是O(n²)時間複雜度實在是難以接受的。但是對於逆序對問題，卻有一個看似不想關的演算法來解決–歸併排序。時間複雜度和空間複雜度完全與歸併排序一樣，只是在歸併過程中，添加了一個變數，對於逆序對的數目進行了記錄。這樣就將時間複雜度降低到了O(nlogn)。

原理

因為逆序對的數目可能存在平方數個逆序對，因此要想將逆序對數目求解的複雜度降低到O(nlogn)，就不能對每一個逆序對進行計算。根據歸併排序思想，使用歸併求解逆序對時，將會在將兩個有序數組合併成一個有序陣列的過程中，記錄逆序對的數目，其他如陣列劃分和排序過程同歸並排序。

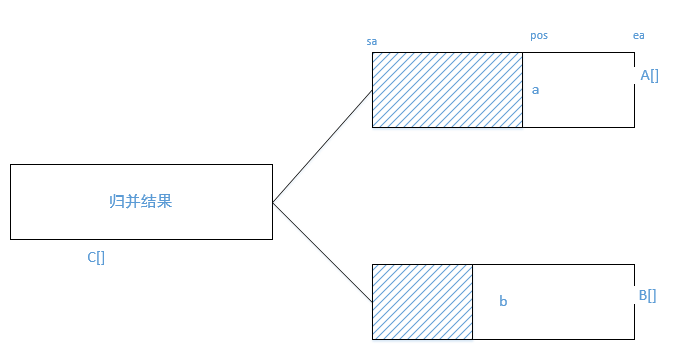
在歸併排序的合併步驟中，假設將兩個有序陣列A[] 和有序陣列B[] 和併為一個有序陣列C[]。計算逆序對問題轉換為計算逆序對(a,b)的問題，其中a來自A[], b來自B[]。當a < b的時候，不計數，當a>b的時候(a,b)就是逆序對，由於A[]是有序的，那麼A[]中位於a之後的元素對於B[]中的元素b也形成了逆序對，於是對於逆序對(a,b)，（假設A[]的起始下標為sa,結束下標為ea,a的下標為pos）實際上合併成C[]後會會產生ea-pos+1個逆序對。

也就是說，合併過程中，每次出現一對這樣的(a,b),逆序對數目sum = sum + ea-pos+1 ;

示例程式碼

    #include<iostream>

    #define N 100000

    using namespace std;

    void merge(int arr[],int start,int mid,int end,int temp[],long long *count){
        int index = 0,index1 = 0,index2 = 0;
        index = 0
 
; index1 = start; index2 = mid+1;

        while((index1<=mid) && (index2<=end)){
            if(arr[index1] <= arr[index2]){
                temp[index++] = arr[index1++];
            }
            else{
                temp[index++] = arr[index2++];
                //ans+=e1-p1+1;
                (*count) = (*count) + mid - index1 + 1;
            }
        }
        while(index1<=mid)
            temp[index++] = arr[index1++];
        while(index2<=end)
            temp[index++] = arr[index2++];

        for(int i=0;i<index;i++){
            // 複製也是遞迴進行的，所以並不是從start開始到end
            arr[start+i] = temp[i];
        }
    }

    void mergeSort(int arr[],int start,int end,int temp[],long long *count){
        if(start<end){ // 遞迴出口
            int mid = 0;
            mid = (start+end)>>1;
            mergeSort(arr,start,mid,temp,count);
            mergeSort(arr,mid+1,end,temp,count);
            merge(arr,start,mid,end,temp,count);
        }
    }
    int main(){
        long long count = 0;
        int m = 0;
        cin>>m;
        int *a = new int[m];
        for(int i=0;i<m;i++){
            cin>>a[i];
        }

        int *temp = new int[m];
        mergeSort(a,0,m-1,temp,&count);
        delete []a;
        delete []temp;
        cout<<count<<endl;

        return 0;
    }

輸入格式為：先輸入一個數字代表陣列的長度，回車，接下來依次輸入以空格分割的n個數組元素。輸出就是該陣列的逆序對數目。