歸併排序

歸併問題按照分治三步法進行介紹：
劃分問題：把序列分成元素個數儘量相等的兩半
遞迴求解：把兩半元素分別排序
合併問題：把兩個有序表合併成一個
借鑑一個部落格的圖
圖解排序演算法(四)之歸併排序

分而治之

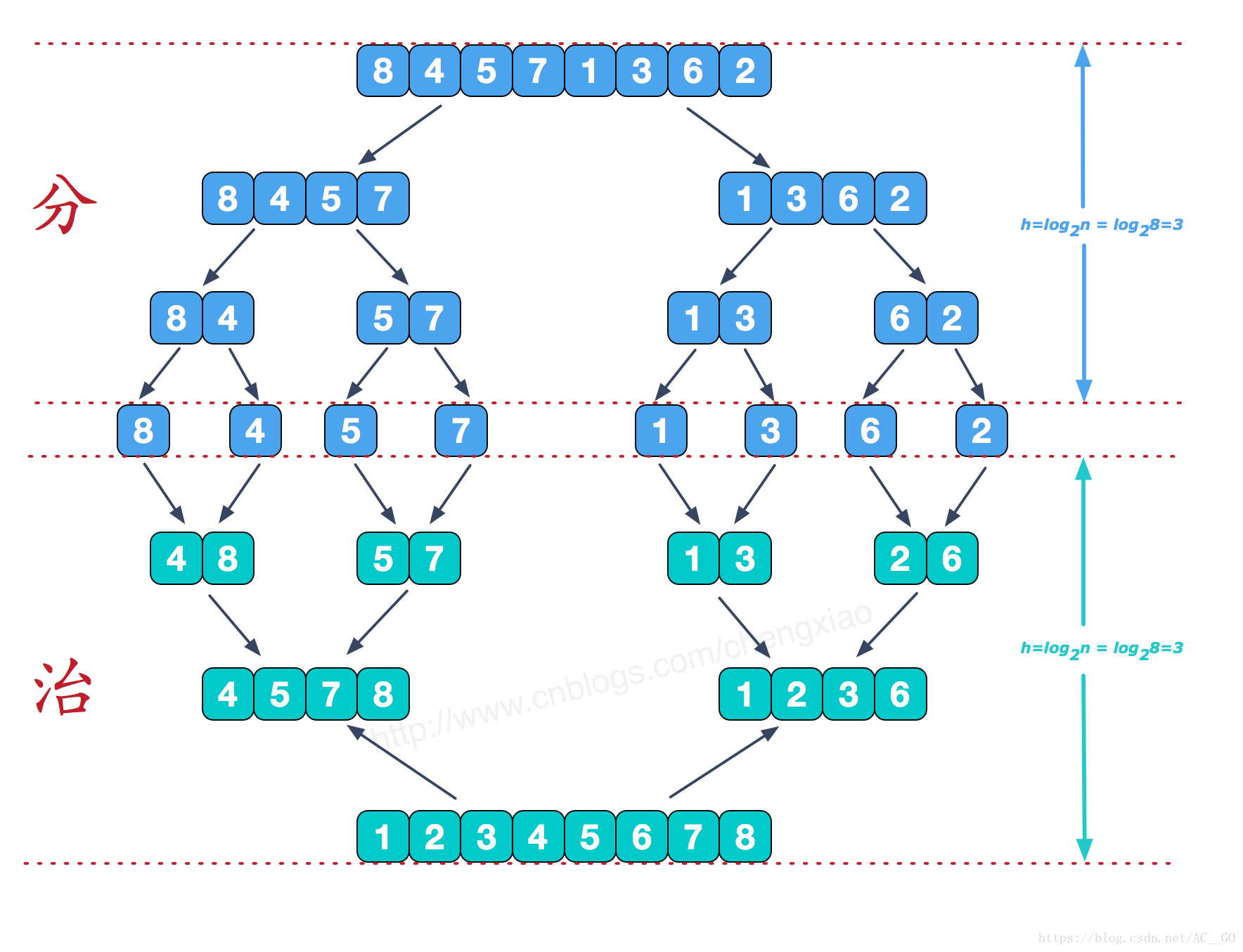
可以看到這種結構很像一棵完全二叉樹，本文的歸併排序我們採用遞迴去實現（也可採用迭代的方式去實現）。分階段可以理解為就是遞迴拆分子序列的過程，遞迴深度為log2n。

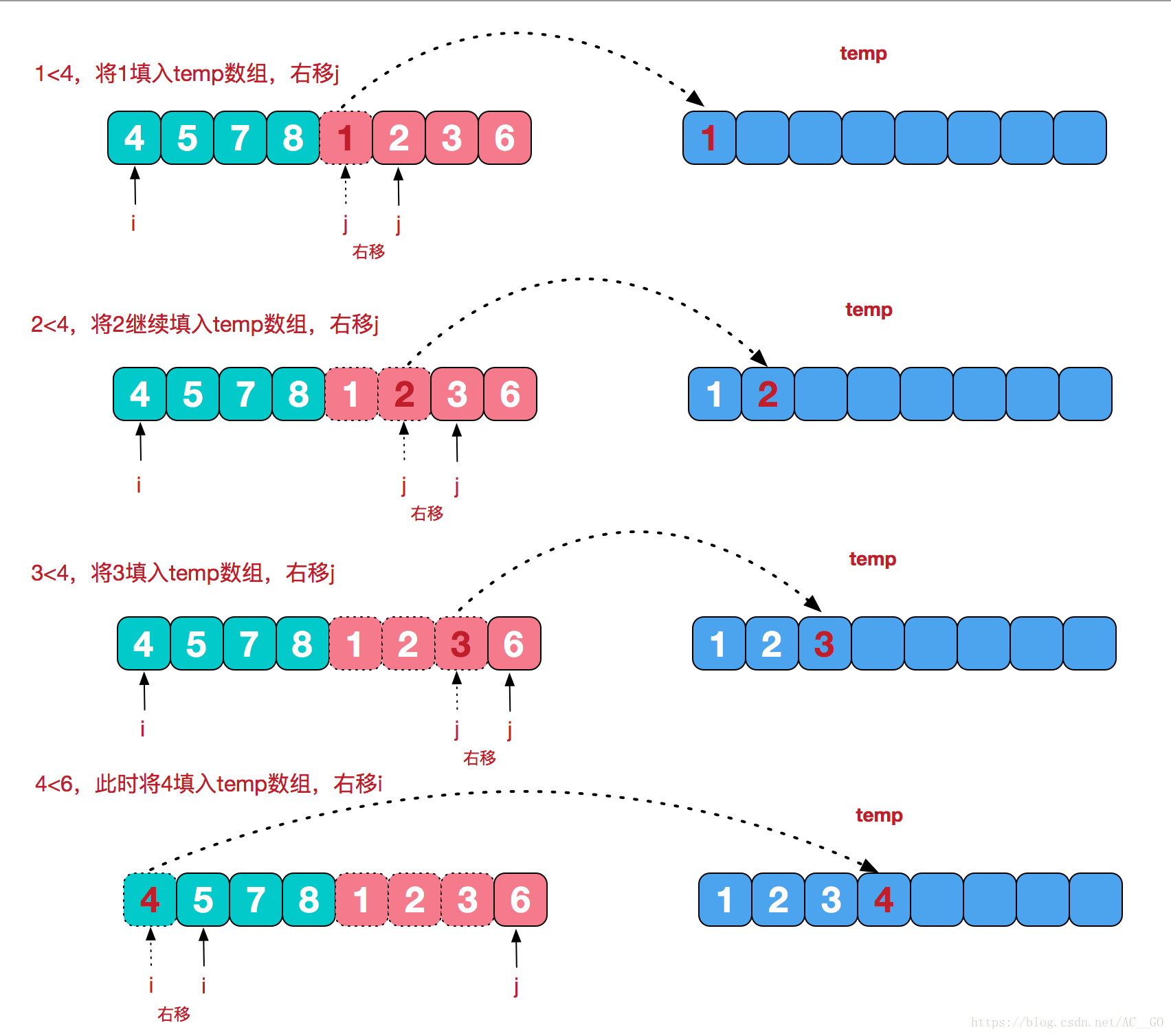
合併相鄰有序子序列

再來看看治階段，我們需要將兩個已經有序的子序列合併成一個有序序列，比如上圖中的最後一次合併，要將[4,5,7,8]和[1,2,3,6]兩個已經有序的子序列，合併為最終序列[1,2,3,4,5,6,7,8]，來看下實現步驟。

再借鑑一個部落格的程式碼：
白話經典算法系列之五 歸併排序的實現（講的真好）
首先考慮下如何將將二個有序數列合併。這個非常簡單，只要從比較二個數列的第一個數，誰小就先取誰，取了後就在對應數列中刪除這個數。然後再進行比較，如果有數列為空，那直接將另一個數列的資料依次取出即可。

//將有序陣列a[]和b[]合併到c[]中  
void MemeryArray(int a[], int n, int b[], int m, int c[])  
{  
    int i, j, k;  

    i = j = k = 0;  
    while (i < n && j < m)  
    {  
        if
 
 (a[i] < b[j])  
            c[k++] = a[i++];  
        else  
            c[k++] = b[j++];   
    }  

    while (i < n)  
        c[k++] = a[i++];  

    while (j < m)  
        c[k++] = b[j++];  
}  

可以看出合併有序數列的效率是比較高的，可以達到O(n)。

解決了上面的合併有序數列問題，再來看歸併排序，其的基本思路就是將陣列分成二組A，B，如果這二組組內的資料都是有序的，那麼就可以很方便的將這二組資料進行排序。如何讓這二組組內資料有序了？

可以將A，B組各自再分成二組。依次類推，當分出來的小組只有一個數據時，可以認為這個小組組內已經達到了有序，然後再合併相鄰的二個小組就可以了。這樣通過先遞迴的分解數列，再合併數列就完成了歸併排序。

//將有二個有序數列a[first...mid]和a[mid...last]合併。  
void mergearray(int a[], int first, int mid, int last, int temp[])  
{  
    int i = first, j = mid + 1;  
    int m = mid,   n = last;  
    int k = 0;  

    while (i <= m && j <= n)  
    {  
        if (a[i] <= a[j])  
            temp[k++] = a[i++];  
        else  
            temp[k++] = a[j++];  
    }  

    while (i <= m)  
        temp[k++] = a[i++];  

    while (j <= n)  
        temp[k++] = a[j++];  

    for (i = 0; i < k; i++)  
        a[first + i] = temp[i];  
}  
void mergesort(int a[], int first, int last, int temp[])  
{  
    if (first < last)  
    {  
        int mid = (first + last) / 2;  
        mergesort(a, first, mid, temp);    //左邊有序  
        mergesort(a, mid + 1, last, temp); //右邊有序  
        mergearray(a, first, mid, last, temp); //再將二個有序數列合併  
    }  
}  

bool MergeSort(int a[], int n)  
{  
    int *p = new int[n];  
    if (p == NULL)  
        return false;  
    mergesort(a, 0, n - 1, p);  
    delete[] p;  
    return true;  
}  

看了劉汝佳的演算法競賽入門經典，發現了更簡潔的寫法。貼出程式碼和解釋：

CODE：

#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <iostream>
#include <algorithm>
#include <cmath>
using namespace std;
const int maxn = 1000;
void merge_sort(int* A, int x,int y, int* T)
{
    if(y-x > 1)
    {
        int m = x + (y-x)/2;
        int p = x, q = m, i = x;//p為合併時左邊下標，q為右邊下標
        merge_sort(A, x, m, T);//左邊排序
        merge_sort(A, m, y, T);//右邊排序
        while(p < m || q < y){//只要有一個序列非空就要繼續合併陣列
            if(q >= y || (p < m && A[p] <= A[q]))//如果
                T[i++] = A[p++];//從左邊陣列複製到臨時空間
            else
                T[i++] = A[q++];//從右邊陣列複製到臨時空間
        }
        for(i = x; i < y; i++)
            A[i] = T[i];//從輔助空間複製回A陣列
    }
}

int main()
{
    int n;
    int A[maxn], T[maxn];
    cin >> n;
    for(int i = 0; i < n; i++)
        cin >> A[i];
    merge_sort(A,0,n,T);
    for(int i = 0; i < n; i++)
        cout << A[i] << ' ';
    return 0;
}

逆序對

在歸併排序的合併步驟中，假設將兩個有序陣列A[] 和有序陣列B[] 和併為一個有序陣列C[]。計算逆序對問題轉換為計算逆序對(a,b)的問題，其中a來自A[], b來自B[]。當a < b的時候，不計數，當a>b的時候(a,b)就是逆序對，由於A[]是有序的，那麼A[]中位於a之後的元素對於B[]中的元素b也形成了逆序對，於是對於逆序對(a,b)，（假設A[]的起始下標為sa,結束下標為ea,a的下標為pos）實際上合併成C[]後會會產生ea-pos+1個逆序對。

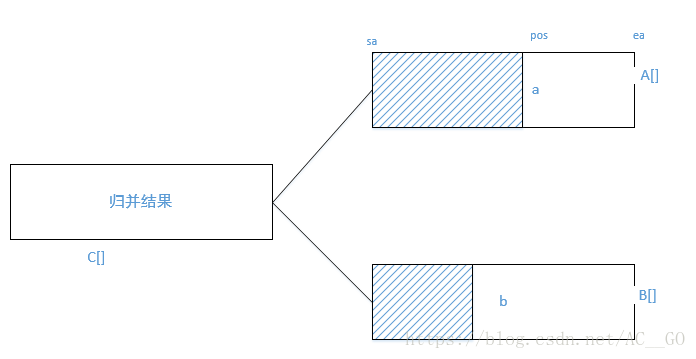
也就是說，合併過程中，每次出現一對這樣的(a,b),逆序對數目sum = sum + ea-pos+1 ;
根據這樣的原理，再給予對歸併排序的理解，將上面的計算公式加入到歸併排序中，就可以在O(nlogn)的時間複雜度裡計算出一個給定數字序列中逆序對的數目。

再看劉汝佳的描述：
只要對於右邊的每個j，統計左邊比它大的元素個數f(j)，則所有f(j)之和便是答案。
由於合併操作是從小到大進行的，當右邊的A[j]複製到T中時，左邊還沒來得及複製到T的那些數就是左邊所有比A[j]大的數
在歸併排序的程式碼的基礎上
將else T[i++] = A[q++];改為else{T[i++] = A[q++];cnt += m-p}。在呼叫前應給cnt清零。
程式碼按上面描述改一下就可以了

CODE

#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <iostream>
#include <algorithm>
#include <cmath>
using namespace std;
const int maxn = 1000;
int cnt;
void merge_sort(int* A, int x,int y, int* T)
{
    if(y-x > 1)
    {
        int m = x + (y-x)/2;
        int p = x, q = m, i = x;//p為合併時左邊下標，q為右邊下標
        merge_sort(A, x, m, T);//左邊排序
        merge_sort(A, m, y, T);//右邊排序
        while(p < m || q < y){//只要有一個序列非空就要繼續合併陣列
            if(q >= y || (p < m && A[p] <= A[q]))//如果
                T[i++] = A[p++];//從左邊陣列複製到臨時空間
            else
            {
                T[i++] = A[q++];//從右邊陣列複製到臨時空間
                cnt +=m-p;
            }
        }
        for(i = x; i < y; i++)
            A[i] = T[i];//從輔助空間複製回A陣列
    }
}

int main()
{
    int n;
    int A[maxn], T[maxn];
    cin >> n;
    for(int i = 0; i < n; i++)
        cin >> A[i];
    cnt = 0;
    merge_sort(A,0,n,T);
    for(int i = 0; i < n; i++)
        cout << A[i] << ' ';
    cout << endl;
    cout << cnt << endl;
    return 0;
}