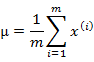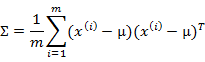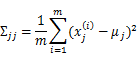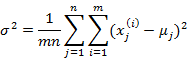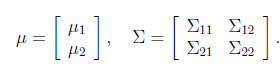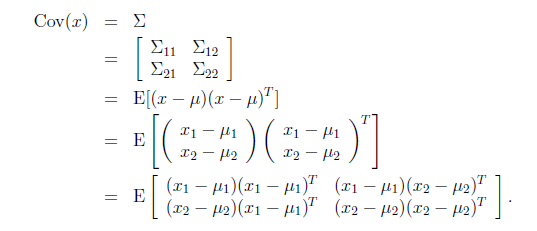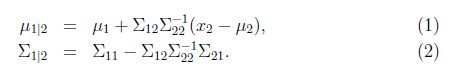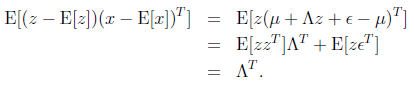因子分析(Factor Analysis)
1 問題
之前我們考慮的訓練資料中樣例![]() 的個數m都遠遠大於其特徵個數n,這樣不管是進行迴歸、聚類等都沒有太大的問題。然而當訓練樣例個數m太小,甚至m<<n的時候,使用梯度下降法進行迴歸時,如果初值不同,得到的引數結果會有很大偏差(因為方程數小於引數個數)。另外,如果使用多元高斯分佈(Multivariate
Gaussian distribution)對資料進行擬合時,也會有問題。讓我們來演算一下,看看會有什麼問題:
的個數m都遠遠大於其特徵個數n,這樣不管是進行迴歸、聚類等都沒有太大的問題。然而當訓練樣例個數m太小,甚至m<<n的時候,使用梯度下降法進行迴歸時,如果初值不同,得到的引數結果會有很大偏差(因為方程數小於引數個數)。另外,如果使用多元高斯分佈(Multivariate
Gaussian distribution)對資料進行擬合時,也會有問題。讓我們來演算一下,看看會有什麼問題:
多元高斯分佈的引數估計公式如下:
分別是求mean和協方差的公式,![]() 表示樣例,共有m個,每個樣例n個特徵,因此
表示樣例,共有m個,每個樣例n個特徵,因此![]() 是n維向量,
是n維向量,![]() 是n*n協方差矩陣。
是n*n協方差矩陣。
當m<<n時,我們會發現![]() 是奇異陣(
是奇異陣(![]() ),也就是說
),也就是說![]() 不存在,沒辦法擬合出多元高斯分佈了,確切的說是我們估計不出來
不存在,沒辦法擬合出多元高斯分佈了,確切的說是我們估計不出來![]() 。
。
如果我們仍然想用多元高斯分佈來估計樣本,那怎麼辦呢?
2 限制協方差矩陣
當沒有足夠的資料去估計![]() 時,那麼只能對模型引數進行一定假設,之前我們想估計出完全的
時,那麼只能對模型引數進行一定假設,之前我們想估計出完全的![]() (矩陣中的全部元素),現在我們假設
(矩陣中的全部元素),現在我們假設![]() 就是對角陣(各特徵間相互獨立),那麼我們只需要計算每個特徵的方差即可,最後的
就是對角陣(各特徵間相互獨立),那麼我們只需要計算每個特徵的方差即可,最後的![]() 只有對角線上的元素不為0
只有對角線上的元素不為0
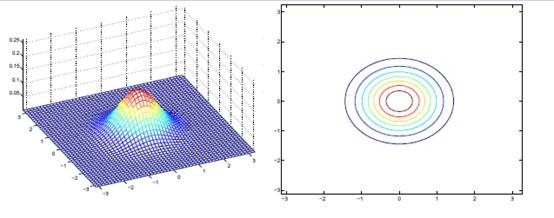
回想我們之前討論過的二維多元高斯分佈的幾何特性,在平面上的投影是個橢圓,中心點由![]() 決定,橢圓的形狀由
決定,橢圓的形狀由![]() 決定。
決定。![]() 如果變成對角陣,就意味著橢圓的兩個軸都和座標軸平行了。
如果變成對角陣,就意味著橢圓的兩個軸都和座標軸平行了。
如果我們想對![]() 進一步限制的話,可以假設對角線上的元素都是等值的。
進一步限制的話,可以假設對角線上的元素都是等值的。
其中
也就是上一步對角線上元素的均值,反映到二維高斯分佈圖上就是橢圓變成圓。
當我們要估計出完整的![]() 時,我們需要m>=n+1才能保證在最大似然估計下得出的
時,我們需要m>=n+1才能保證在最大似然估計下得出的![]() 是非奇異的。然而在上面的任何一種假設限定條件下,只要m>=2都可以估計出限定的
是非奇異的。然而在上面的任何一種假設限定條件下,只要m>=2都可以估計出限定的![]() 。
。
這樣做的缺點也是顯然易見的,我們認為特徵間獨立,這個假設太強。接下來,我們給出一種稱為因子分析的方法,使用更多的引數來分析特徵間的關係,並且不需要計算一個完整的![]() 。
。
3 邊緣和條件高斯分佈
在討論因子分析之前,先看看多元高斯分佈中,條件和邊緣高斯分佈的求法。這個在後面因子分析的EM推導中有用。
假設x是有兩個隨機向量組成(可以看作是將之前的![]() 分成了兩部分)
分成了兩部分)
那麼只知道聯合分佈的情況下,如何求得![]() 的邊緣分佈呢?從上面的
的邊緣分佈呢?從上面的![]() 和
和![]() 可以看出,
可以看出,
由此可見,多元高斯分佈的邊緣分佈仍然是多元高斯分佈。也就是說![]() 。
。
上面Cov(x)裡面有趣的是![]() ,這個與之前計算協方差的效果不同。之前的協方差矩陣都是針對一個隨機變數(多維向量)來說的,而
,這個與之前計算協方差的效果不同。之前的協方差矩陣都是針對一個隨機變數(多維向量)來說的,而![]() 評價的是兩個隨機向量之間的關係。比如
評價的是兩個隨機向量之間的關係。比如![]() ={身高,體重},
={身高,體重},![]() ={性別,收入},那麼
={性別,收入},那麼![]() 求的是身高與身高,身高與體重,體重與體重的協方差。而
求的是身高與身高,身高與體重,體重與體重的協方差。而![]() 求的是身高與性別,身高與收入,體重與性別,體重與收入的協方差,看起來與之前的大不一樣,比較詭異的求法。
求的是身高與性別,身高與收入,體重與性別,體重與收入的協方差,看起來與之前的大不一樣,比較詭異的求法。
上面求的是邊緣分佈,讓我們考慮一下條件分佈的問題,也就是![]() 的問題。根據多元高斯分佈的定義,
的問題。根據多元高斯分佈的定義,![]() 。
。
且
這是我們接下來計算時需要的公式,這兩個公式直接給出,沒有推導過程。如果想了解具體的推導過程,可以參見Chuong B. Do寫的《Gaussian processes》。
4 因子分析例子
下面通過一個簡單例子,來引出因子分析背後的思想。
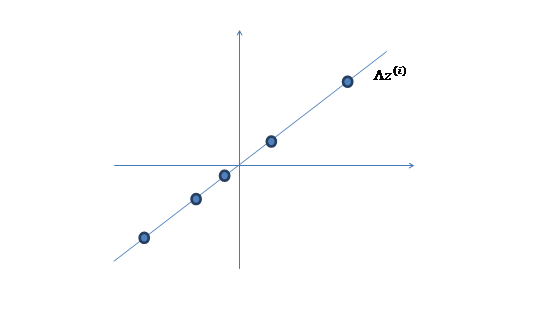
1、 首先在一個k維的空間中按照多元高斯分佈生成m個![]() (k維向量),即
(k維向量),即
4、 由於真實樣例![]() 與上述模型生成的有誤差,因此我們繼續加上誤差
與上述模型生成的有誤差,因此我們繼續加上誤差![]() (n維向量),
(n維向量),
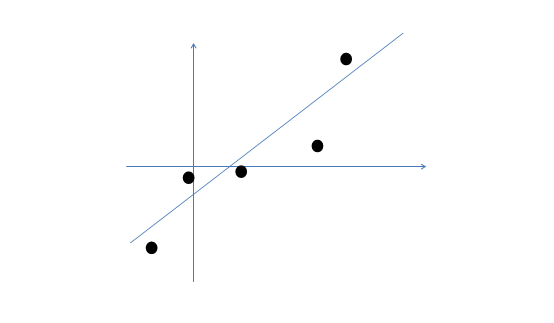
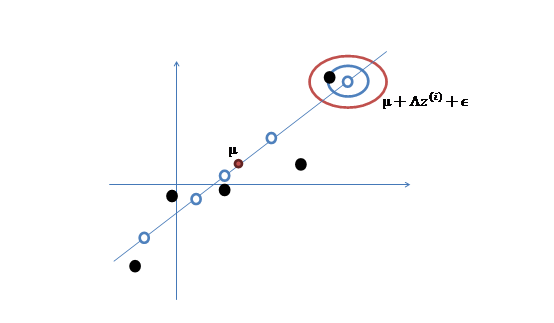
讓我們使用一種直觀方法來解釋上述過程:
那麼按照因子分析的理解,樣本點的生成過程如下:
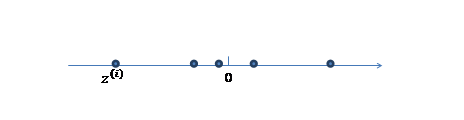
1、 我們首先認為在1維空間(這裡k=1),存在著按正態分佈生成的m個點![]() ,如下
,如下
均值為0,方差為1。
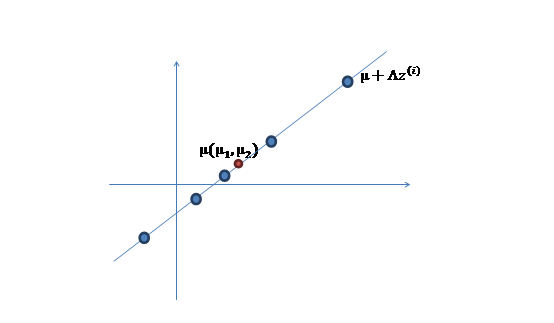
3、 之後加上![]() ,即將所有點的橫座標移動
,即將所有點的橫座標移動![]() ,縱座標移動
,縱座標移動![]() ,將直線移到一個位置,使得直線過點
,將直線移到一個位置,使得直線過點![]() ,原始左邊軸的原點現在為
,原始左邊軸的原點現在為![]() (紅色點)。
(紅色點)。
然而,樣本點不可能這麼規則,在模型上會有一定偏差,因此我們需要將上步生成的點做一些擾動(誤差),擾動![]() 。
。
5、 其中由於z和![]() 的均值都為0,因此
的均值都為0,因此![]() 也是原始樣本點(黑色點)的均值。
也是原始樣本點(黑色點)的均值。
由以上的直觀分析,我們知道了因子分析其實就是認為高維樣本點實際上是由低維樣本點經過高斯分佈、線性變換、誤差擾動生成的,因此高維資料可以使用低維來表示。
5 因子分析模型
上面的過程是從隱含隨機變數z經過變換和誤差擾動來得到觀測到的樣本點。其中z被稱為因子,是低維的。
我們將式子再列一遍如下:
下面使用的因子分析表示方法是矩陣表示法,在參考資料中給出了一些其他的表示方法,如果不明白矩陣表示法,可以參考其他資料。
矩陣表示法認為z和x聯合符合多元高斯分佈,如下
我們已知E[z]=0,因此
接著求
1 問題
之前我們考慮的訓練資料中樣例的個數m都遠遠大於其特徵個數n,這樣不管是進行迴歸、聚類等都沒有太大的問題。然而當訓練樣例個數m太小,甚至m<<n的時候,使用梯度下降法進行迴歸時,如果初值不同,得到的引數結果會有很大偏差(因為方程數小於引數個
1 問題
之前我們考慮的訓練資料中樣例的個數m都遠遠大於其特徵個數n,這樣不管是進行迴歸、聚類等都沒有太大的問題。然而當訓練樣例個數m太小,甚至m<<n的時候,使用梯度下降法
因子分析(Factor Analysis)
首先從原理上說,主成分分析是試圖尋找原有自變數的一個線性組合。這個組合方差要大,那麼攜帶的資訊也就多,也就是相當於把原始資料的主要成分給拿了出來。
而因子分析,是從假設出發,它是假設所有的自變數x出現的原因是因為背後存在一個潛變數f,即因 name 大量 tex 管理 ref 分析 一個 之間 ora
因子分析與因子分析法主成分分析通過線性組合將原變量綜合成幾個主成分,用較少的綜合指標來代替原來較多的指標(變量)。在多變量分析中,某些變量間往往存在相關性。是什麽原因使變量間有關聯呢?是否存在不能直接觀測到的 svd分解 主成分分析 http src inf 因子分析 分解 spa span
並且SVD分解也適用於一般的矩陣。
主成分分析和因子分析(未完成)
一、情感分析簡述
情感分析(sentiment analysis),又叫意見抽取(opinion extraction),意見挖掘(opinion mining),情感挖掘(sentiment mining)以及主觀分析(subjectivity analysis)。
情感分
何為分類分析
在機器學習和統計中,分類是基於包含其類別成員資格已知的觀察(或例項)的訓練資料集來識別新觀察所屬的一組類別(子群體)中的哪一個的問題。例如,將給定的電子郵件分配給“垃圾郵件”或“非垃圾郵件”類,並根據觀察到的患者特徵(性別,血壓,某些症狀的存在或不存在等)為給定患者分配
何為聚類分析
聚類分析或聚類是對一組物件進行分組的任務,使得同一組(稱為聚類)中的物件(在某種意義上)與其他組(聚類)中的物件更相似(在某種意義上)。它是探索性資料探勘的主要任務,也是統計 資料分析的常用技術,用於許多領域,包括機器學習,模式識別,影象分析,資訊檢索,生物資訊學,資料
一、課程介紹
斯坦福大學於2012年3月在Coursera啟動了線上自然語言處理課程,由NLP領域大牛Dan Jurafsky 和 Chirs Manning教授授課:https://class.coursera.org/nlp/
以下是本課程的學習筆記,以課程PP
迫於專案和實驗室事務,需要做一點工程物探相關的內容。(隱寫分析只能先往後稍稍了。。。)略讀一些參考文獻,梳理一下專案背景。
在之前的一些專案中,面波(surface wave),或者叫ground-roll wave(地滾波),通常是被作為干擾反射訊號的強振幅噪聲需要進行衰
因子分析
因子分析(Factor Analysis)是指研究從變數群中提取共性因子的統計技術,這裡的共性因子指的是不同變數之間內在的隱藏因子。例如,一個學生的英語、資料、語文成績都很好,那麼潛在的共 pos spa com strong 版本 url tro href http 團隊作業10——事後分析(Beta版本)
http://www.cnblogs.com/newteam6/p/6953992.html
團隊作業10——復審(Beta版本)
http:// 隨著 測試 到你 屬於 一次 有感 如何解決 lsp 資源 設想和目標
1.我們的軟件要解決什麽問題?是否定義得很清楚?是否對典型用戶和典型場景有清晰的描述?
解決用戶想要隨時鍛煉四則運算能力的問題;定義的很清楚;有清晰描述。
2.是否有充足的時間來做計劃?
有時間,在al 取消 spa 控制 server 信息 des 包含 flash poi 一、訪問入口
http://open.weibo.com/wiki/%E6%8E%88%E6%9D%83%E6%9C%BA%E5%88%B6%E8%AF%B4%E6%98%8E
微博開放接口的 mage -s ret 增刪 函數 tno png log 唯一性 一、HashMap簡介
HashMap是一種基於數組+鏈表+紅黑樹的數據結構,其中紅黑樹部分在JDK1.8後引入,當鏈表長度大於8的時候轉換為紅黑樹。
HashMap繼承於AbstractMap(M oss sub 性能檢測 數據庫 ble group 檢查 自己 情況 explain關鍵字結果
列名所代表的的含義:
Id:MySQL QueryOptimizer 選定的執行計劃中查詢的序列號。表示查詢中執行 select 子句或操作表的順序,id 值越大優先級越高,越 tro 滿足 並查集 con name font http -s esp 原題鏈接:https://www.luogu.org/problem/show?pid=1955
夏令營的模擬考試題,今天才發現是NOI原題,沒想到15年也有這樣裸的題。。。
離散化一下,這樣就能 語言 的人 感覺 哪些 開發 tps 部分 界面 發現 第一部分 調研,評測
評測:
軟件的bug,功能評測,黑箱測試
1.下載並使用,描述最簡單直觀的個人第一次上手體驗。
界面簡潔明了,把項目列表放在首頁最顯眼的位置。而且整體感覺很舒適,讓人第一感官很舒服。
2.按照描 arc 是不是 合作 一個 決定 例如 工具 角色 教訓 設想和目標
1. 我們的軟件要解決什麽問題?是否定義得很清楚?是否對典型用戶和典型場景有清晰的描述?
單個系統的部分功能 是 是
2. 我們達到目標了麽(原計劃的功能做到了幾個? 按照原計劃交付時間交 C++ 逗號表達式 重載逗號操作符 我們之前在 C 語言中也學習過了逗號表達式,那麽我們就先來再次重新看看逗號表達式。逗號操作符(,)可以構成逗號表達式,逗號表達式用於將多個子表達式連接為一個表達式,它的值為最後一個子表達式的值。逗號表達式中的前 N-1 個子表達式可以沒有返回值, ![]()
相關推薦
【機器學習-斯坦福】因子分析(Factor Analysis)
因子分析(Factor Analysis)
因子分析(factor analysis)
因子分析法(Factor Analysis)是什麽分析
主成分分析和因子分析(未完成)
斯坦福大學-自然語言處理入門 筆記 第七課 情感分析(sentiment analysis)
python資料分析:分類分析(classification analysis)
python資料分析:聚類分析(cluster analysis)
斯坦福大學自然語言處理第七課“情感分析(Sentiment Analysis)”
工程物探中的地震波面波多道分析(Multichannel analysis of surface waves, MASW)簡介
sklearn因子分析(python)
團隊作業10——復審和事後分析(Beta版本)
事後諸葛亮分析(Beta階段)
apigw鑒權分析(1-4)新浪微博開放平臺 - 鑒權分析
HashMap源碼分析(JDK1.8)
sql性能分析(explain關鍵字)
NOI2015 程序自動分析(luogu p1955)
個人作業——軟件產品案例分析(待更)
團隊作業9——事後分析(Beta版本)
逗號操作符重載分析(三十三)