2. 程式人生 > >AVL樹Java實現

AVL樹Java實現

阿新 • • 發佈：2019-01-02

歡迎探討，如有錯誤敬請指正

如需轉載，請註明出處http://www.cnblogs.com/nullzx/

1. AVL定義

AVL樹是一種改進版的搜尋二叉樹。對於一般的搜尋二叉樹而言，如果資料恰好是按照從小到大的順序或者從大到小的順序插入的，那麼搜尋二叉樹就對退化成連結串列，這個時候查詢，插入和刪除的時間都會上升到O(n)，而這對於海量資料而言，是我們無法忍受的。即使是一顆由完全隨機的資料構造成的搜尋二叉樹，從統計角度去分析，在進行若甘次的插入和刪除操作，這個搜尋二叉樹的高度也不能令人滿意。這個時候大家就希望能有一種二叉樹解決上述問題。這個時候就出現平衡搜尋二叉樹，它的基本原理就是在插入和刪除的時候，根據情況進行調整，以降低二叉樹的高度。平衡搜尋二叉樹典型代表就是AVL樹和紅黑樹。

AVL樹：任何一個節點的左子支高度與右子支高度之差的絕對值不超過1。需要我們注意的是，AVL樹定義不是說從根節點到葉子節點的最短距離比最長短距離大1。

image

上圖就是一顆AVL樹，從根節點到葉子節點的最短距離是5，最長距離是9。

2. 旋轉的定義

因為每種書中對旋轉的定義不一致，所以我們有必要在這裡特此說明一下

以某一個節點為軸，它的左子枝順時針旋轉，作為新子樹的根，我們稱之為順時針旋轉（clockwise）或者右旋轉。

同理，以某一個節點為軸，它的右子枝逆針旋轉，作為新子樹的根，我們稱之為逆時針旋轉（anticlockwise）或者左旋轉。

3. AVL插入操作

AVL樹的插入操作首先會按照普通搜尋二叉樹的插入操作進行，當插入一個數據後，我們會沿著插入資料時所經過的的節點回溯，回溯的過程中會判回溯路徑中的每個節點的左子支高度與右子支高度之差的絕對值是否超過1，如果超過1我們就進行調整，調整的目的是使得該節點滿足AVL樹的定義。調整的情況可以分為以下四旋轉操作，旋轉操作可以降低樹的高度，同時不改變搜尋二叉樹的性質（即任何一個節點左子支中的全部節點小於該節點，右子支的全部節點大於該節點）。

3.1 情況1

節點X左子支比右子支高度大2，且插入的節點位於X的左孩子節點XL的左子支上

image

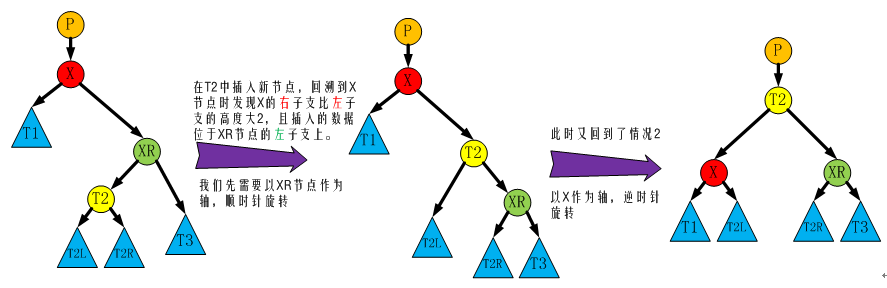
3.2 情況2

節點X右子支比左子支高度大2，且插入的節點位於節點X右孩子節點XR的右子支上

image

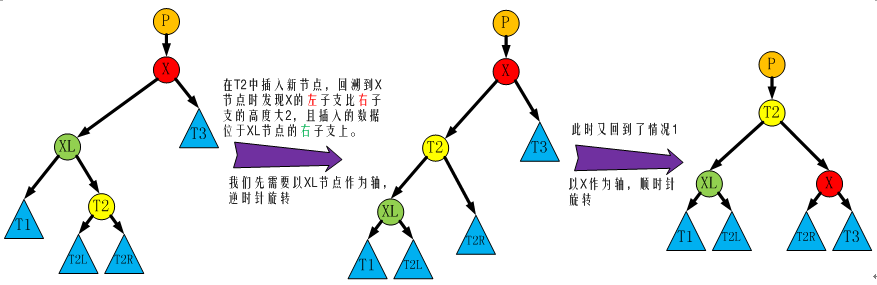
3.3 情況3

節點X左子支比右子支高度大2，且插入的節點位於節點X左孩子節點XL的右子支上

image

3.4 情況4

節點X左子支比右子支高度大2，且插入的節點位於節點X左孩子節點XL的右子支上

image

4. AVL刪除操作

AVL樹的刪除操作和插入操作一樣，首先會按照普通搜尋二叉樹的刪除操作進行，當刪除一個數據後，和插入操作一樣，我們通常採取的策略是沿著刪除資料時所經過的的節點回溯，回溯的過程中會判斷該節點的左子支高度與右子支高度之差的絕對值是否超過1（或者說大2），如果超過1，我們就進行調整，調整的目的是使得該節點滿足AVL樹的定義。調整的情況可以分為四種，和插入過程完全一樣，這裡不在贅述。


package datastruct;
 
import java.util.Comparator;
 
public class AVLtree <E>{
    private static class Node<E>{
        int h;
        E element;
        Node<E> left;
        Node<E> right;
        //由於java中不像C語言那樣有二級指標的概念，所以新增一個父類的引用，方便程式編寫
        Node<E> parent;
         
        public Node(E element, int h, Node<E> left, Node<E> right, Node<E> parent){
            this.element = element;
            this.h = h;
            this.left = left;
            this.right = right;
            this.parent = parent;
        }
    }
     
    private Node<E> root;//指向偽根節點的引用
    private int size = 0;//節點個數
    Comparator<? super E> cmp;//節點大小的比較器
     
    //如果呼叫了不帶引數的建構函式，則使用該內部類作為比較器，
    //但此時泛型E需要繼承Comparable介面,否則執行時會丟擲異常
    private static class Cmp<T> implements Comparator<T>{
        @SuppressWarnings({ "unchecked", "rawtypes" })
        @Override
        public int compare(T e1, T e2) {
            return ((Comparable)e1).compareTo(e2);
        }
         
    }
     
    //帶比較器的建構函式
    public AVLtree(Comparator<? super E> cmp){
        if(cmp == null){
            throw new IllegalArgumentException();
        }
        this.cmp = cmp;
        //建立一個偽根節點，該節點的右子支才是真正的AVL樹的根
        //使用偽根節點節點的目的是，對插入和刪除操作遞迴的形式能夠統一
        root = new Node<E>(null, -1, null, null, null);
    }
     
    //不帶比較器的建構函式
    public AVLtree(){
        this.cmp = new Cmp<E>();
        root = new Node<E>(null, -1, null, null, null);
    }
     
    //如果樹中節點有變動，從底向上逐級呼叫該函式，可以更新節點的高度
    private int getHight(Node<E> x){
        if(x == null){
            return 0;
        }else{
            return x.h;
        }
    }
     
    //求某個節點作為根時，該子樹的最小值
    private E treeMin(Node<E> x){
        while(x.left != null){
            x = x.left;
        }
        return x.element;
    }
     
    public int size(){
        return size;
    }
     
    //先根遍歷，除錯時使用
    public void preorderTraverse(){
        if(root != null){
            preorderTraverse0(root.right);
        }
    }
     
    private void preorderTraverse0(Node<E> x){
        if(x != null){
            System.out.print(x.element+" ");
            if(x.left != null){
                System.out.print(x.left.element+" ");
            }else{
                System.out.print("null  ");
            }
             
            if(x.right != null){
                System.out.print(x.right.element+" ");
            }else{
                System.out.print("null  ");
            }
            System.out.println();
            preorderTraverse0(x.left);
            preorderTraverse0(x.right);
        }
    }
     
    //逆時針旋轉（左旋），引數表示軸節點
    private void antiClockwiseRotate(Node<E> X){
        Node<E> P = X.parent;
        Node<E> XR = X.right;
        if(P.left == X){
            P.left = XR;
        }else{
            P.right = XR;
        }
        XR.parent = P;
         
        X.right = XR.left;
        if(XR.left != null){
            XR.left.parent = X;
        }
         
        XR.left = X;
        X.parent = XR;
         
        //旋轉後要更新這兩個節點的高度
        X.h = Math.max(getHight(X.left), getHight(X.right)) + 1;
        XR.h = Math.max(getHight(XR.left), getHight(XR.right)) + 1;
    }
     
    //順時針旋轉（右旋）,引數表示軸節點
    private void clockwistRotate(Node<E> X){
        Node<E> P = X.parent;
        Node<E> XL = X.left;
        if(P.left == X){
            P.left = XL;
        }else{
            P.right = XL;
        }
        XL.parent = P;
         
        X.left = XL.right;
        if(XL.right != null){
            XL.right.parent = X;
        }
         
        XL.right = X;
        X.parent = XL;
         
        //旋轉後要更新這兩個節點的高度
        X.h = Math.max(getHight(X.left), getHight(X.right)) + 1;
        XL.h = Math.max(getHight(XL.left), getHight(XL.right)) + 1;
    }
     
    //
    public void insert(E e){
        insert0(root.right, e);
    }
     
    private void insert0(Node<E> x, E e){
        if(x == null){
            root.right = new Node<E>(e, 1, null, null, root);//根節點
            size++;
            return;
        }
         
        if(cmp.compare(e, x.element) > 0){
            if(x.right != null){
                insert0(x.right, e);
                int lh = getHight(x.left);
                int rh = getHight(x.right);
                if(rh - lh == 2){
                    if(cmp.compare(e, x.right.element) > 0){
                        antiClockwiseRotate(x);
                    }else{
                        clockwistRotate(x.right);
                        antiClockwiseRotate(x);
                    }
                }
            }else{
                size++;
                x.right = new Node<E>(e, 1, null, null, x);
            }
        }else
        if(cmp.compare(e, x.element) < 0){
            if(x.left != null){
                insert0(x.left, e);
                int lh = getHight(x.left);
                int rh = getHight(x.right);
                if(lh - rh == 2){
                    if(cmp.compare(e, x.left.element) < 0){
                        clockwistRotate(x);
                    }else{
                        antiClockwiseRotate(x.left);
                        clockwistRotate(x);
                    }
                }
            }else{
                size++;
                x.left = new Node<E>(e, 1, null, null, x);
            }
        }else{
            //元素已存在，我們用新的元素更新舊，
            //compare返回值等於0,並不表示兩個物件完全相等
            x.element = e;
        }
        x.h = Math.max(getHight(x.left), getHight(x.right)) + 1;
    }
     
    public boolean delete(E e){
        return delete0(root.right, e);
    }
     
    //返回值表示是否刪除成功
    private boolean delete0(Node<E> x, E e){
        if(x == null){//沒有找到待刪除的元素
            return false;
        }
         
        if(cmp.compare(e, x.element) > 0){
            boolean reval = delete0(x.right, e);
            if(reval == false){
                return false;
            }
             
            int lh = getHight(x.left);
            int rh = getHight(x.right);
            if(lh - rh == 2){
                if(getHight(x.left.left) > getHight(x.left.right)){
                    clockwistRotate(x);
                }else{
                    antiClockwiseRotate(x.left);
                    clockwistRotate(x);
                }
            }
        }else
        if(cmp.compare(e, x.element) < 0){
            boolean reval = delete0(x.left, e);
            if(reval == false){
                return false;
            }
 
            int lh = getHight(x.left);
            int rh = getHight(x.right);
            if(rh - lh == 2){
                if(getHight(x.right.right) > getHight(x.right.left)){
                    antiClockwiseRotate(x);
                }else{
                    clockwistRotate(x.right);
                    antiClockwiseRotate(x);
                }
            }
        }else{//找到待刪除的元素
            Node<E> P = x.parent;
             
            if(x.left == null){//左子支為空，可直接刪除，在這一層一定不需要旋轉
                size--;
                if(P.left == x){
                    P.left = x.right;
                    if(P.left != null){
                        P.left.parent = P;
                    }
                }else{
                    P.right = x.right;
                    if(P.right != null){
                        P.right.parent = P;
                    }
                }
            }else
            if(x.right == null){//右子支為空，可直接刪除，在這一層一定不需要旋轉
                size--;
                if(P.left == x){
                    P.left = x.left;
                    if(P.left != null){                 
                        P.left.parent = P;
                    }
                }else{
                    P.right = x.left;
                    if(P.right != null){
                        P.right.parent = P;
                    }
                }
            }else{//找到待刪除的節點,用後繼節點代替，然後刪除後繼節點
                E nextVal = treeMin(x.right);
                x.element = nextVal;
                delete0(x.right, nextVal);
                int lh = getHight(x.left);
                int rh = getHight(x.right);
                if(lh - rh == 2){
                    if(getHight(x.left.left) > getHight(x.left.right)){
                        clockwistRotate(x);
                    }else{
                        antiClockwiseRotate(x.left);
                        clockwistRotate(x);
                    }
                }
            }
        }
        x.h = Math.max(getHight(x.left), getHight(x.right)) + 1;
        return true;
    }
     
    public static void main(String[] args){
        AVLtree<Integer> avl = new AVLtree<Integer>();
        /*可自行新增插入，刪除操作進行測試*/
        avl.insert(3);
        avl.insert(5);
        avl.insert(6);
        avl.insert(7);
        avl.insert(8);
        avl.insert(9);
        avl.preorderTraverse();
        System.out.println();
        System.out.println(avl.size());
         
        avl.delete(7);
        avl.delete(8);
        avl.preorderTraverse();
        System.out.println();
        System.out.println(avl.size());
    }
}

/**
 * Java 語言: AVL樹
 *
 * @author skywang
 * @date 2013/11/07
 */

public class AVLTreeTest {
    private static int arr[]= {3,2,1,4,5,6,7,16,15,14,13,12,11,10,8,9};

    public static void main(String[] args) {
        int i;
        AVLTree<Integer> tree = new AVLTree<Integer>();

        System.out.printf("== 依次新增: ");
        for(i=0; i<arr.length; i++) {
            System.out.printf("%d ", arr[i]);
            tree.insert(arr[i]);
        }

        System.out.printf("\n== 前序遍歷: ");
        tree.preOrder();

        System.out.printf("\n== 中序遍歷: ");
        tree.inOrder();

        System.out.printf("\n== 後序遍歷: ");
        tree.postOrder();
        System.out.printf("\n");

        System.out.printf("== 高度: %d\n", tree.height());
        System.out.printf("== 最小值: %d\n", tree.minimum());
        System.out.printf("== 最大值: %d\n", tree.maximum());
        System.out.printf("== 樹的詳細資訊: \n");
        tree.print();

        i = 8;
        System.out.printf("\n== 刪除根節點: %d", i);
        tree.remove(i);

        System.out.printf("\n== 高度: %d", tree.height());
        System.out.printf("\n== 中序遍歷: ");
        tree.inOrder();
        System.out.printf("\n== 樹的詳細資訊: \n");
        tree.print();

        // 銷燬二叉樹
        tree.destroy();
    }
}





相關推薦

AVL樹(Java實現)

height sea postorder int void brush node 情況 裏的 AVL樹基本操作 未完....待續.... AVL樹代碼 public class AVLTree<Key extends Comparable<? supe

AVL樹Java實現

歡迎探討，如有錯誤敬請指正 如需轉載，請註明出處http://www.cnblogs.com/nullzx/ 1. AVL定義 AVL樹是一種改進版的搜尋二叉樹。對於一般的搜尋二叉樹而言，如果資料恰好是按照從小到大的順序或者從大到小的順序插入的，那麼搜尋二叉樹就對

JAVA數據結構--AVL樹的實現

oid 非遞歸 max https -a ext 二叉 line 英語 AVL樹的定義 在計算機科學中，AVL樹是最先發明的自平衡二叉查找樹。在AVL樹中任何節點的兩個子樹的高度最大差別為1，所以它也被稱為高度平衡樹。查找、插入和刪除在平均和最壞情況下的時間復雜度都是。增

AVL樹-自平衡二叉查詢樹(Java實現)

      在電腦科學中，AVL樹是最先發明的自平衡二叉查詢樹。AVL樹得名於它的發明者 G.M. Adelson-Velsky 和 E.M. Landis，他們在 1962 年的論文 "An algorithm for the organization of inform

平衡二叉樹AVL樹的實現(c++STL)

pre 根節點 code 先序 blog ltr ons void 過程 #include <iostream> using namespace std; template<class Type> class AVLtree;

數據結構實現（四）二叉查找樹java實現

.com ML treenode 設置 AC getparent 邏輯圖 技術分享 ldb 轉載 http://www.cnblogs.com/CherishFX/p/4625382.html 二叉查找樹的定義： 　　二叉查找樹或者是一顆空樹，或者是一顆具有以下特性的非空二

輸入某二叉樹的前序遍歷和中序遍歷的結果，請重建出該二叉樹(java實現並測試)

假設輸入的前序遍歷和中序遍歷的結果中都不含重複的數字。例如輸入前序遍歷序列{1,2,4,7,3,5,6,8}和中序遍歷序列{4,7,2,1,5,3,8,6}，則重建二叉樹並返回。 package ssp; class TreeNode { int val; TreeNod

AVL樹的實現(程式碼實現)

AVL又叫平衡二叉樹，它是二叉搜尋樹的升級版，為什麼有 平衡二叉樹呢？是因為有些二叉搜尋樹要兼顧查詢和插入的功能，那麼很有可能在插入的情況下，有一種極端情況就是插入的值老是小於根節點，這樣子的話，資料都被插入在了二叉搜尋樹的左側，出現左側一溜下去的情況，這樣的二叉搜尋樹跟個連結串列差不多，查

最優二叉搜尋樹(JAVA實現）

演算法課上老師講的最優二叉搜尋樹，自己又查了些資料才看明白。這篇只記錄下自己用java的實現和自己的一些細節的理解。想學習整個演算法的可以參照 https://blog.csdn.net/zhangyifei521/article/details/50833792 package bes

資料結構之二叉查詢樹Java實現原始碼及註釋

二叉查詢樹（Binary Search Tree），（又：二叉搜尋樹，二叉排序樹）它或者是一棵空樹，或者是具有下列性質的二叉樹： 若它的左子樹不空，則左子樹上所有結點的值均小於它的根結點的值； 若它的右子樹不空，則右子樹上所有結點的值均大於它的根結點的值； 它的左、右子樹也分別為二叉排序樹。以下是樓主用jav

AVL樹C++實現（插入，刪除，查詢，清空，遍歷操作）

AVL.h檔案程式碼 #pragma once #include<iostream> #include<stack> #include <assert.h> using namespace std; using namespace std; template<cl

(模板)AVL樹的實現

#include <iostream> #include <algorithm> using namespace std; class ANode { public: int v, height; //v表示權值,height表示樹的高度 A

AVL樹的實現(完整程式碼)

AVL樹的實現 1.類的架構 public class AvlTree<T extends Comparable<? super T>> { private static class AvlNode<T> { 待實現 } // AVL樹的節點類

二叉搜尋樹Java實現（查詢、插入、刪除、遍歷）

1 class Node { 2 int key; 3 int value; 4 Node leftChild; 5 Node rightChild; 6 7 public Node(int key, int value) { 8

B樹(Java)實現。

import java.util.LinkedList; import java.util.Queue; /** * Created by Kali on 14-5-26.\ * Abstract node. */ public abstract class AbstractBTreeNode<

中序線索二叉樹Java實現

/** * 線索樹結點類 * @author liangxiamoyi * */ public class ThreadNode { /** * 1標識左節點為前驅結點，0標識左節點為左子節點 */ protected int lThread; /**

反轉二叉樹----java實現

實現二叉樹的反轉 示例： 原二叉樹： 4 / \ 2 7 / \ / \ 1 3 6 9 反轉後的二叉樹： 4 / \ 7 2 / \ / \ 9 6 3 1 程式碼實現：（遞迴）

平衡二叉搜尋樹：AVL樹的實現與分析 以及 統一重平衡演算法 （C++）

平衡二叉搜尋樹 既然二叉搜尋樹的效能主要取決於高度,故在節點數目固定的前提下,應儘可能地降低高度。 相應地,應儘可能地使兄弟子樹的高度彼此接近,即全樹儘可能地平衡。 等價變換 等價二叉搜尋樹：若兩棵二叉搜尋樹的中序遍歷序列相同,則稱它們彼此等價;反之亦然。

Python資料結構——AVL樹的實現

遞迴呼叫已到達樹的根。 父節點的平衡因子已調整為零。一旦子樹平衡因子為零，那麼父節點的平衡因子不會發生改變。 我們將實現 AVL 樹的子類BinarySearchTree。首先，我們將重寫_put方法，並寫一個新的輔助方法updateBalance。這些方法如Listing 1 所示。除了第 7 行和第

劍指offer----從上到下列印二叉樹----java實現

題目：從上往下打印出二叉樹的每個節點，同層節點從左至右列印。 思路：其實就是二叉樹的層次遍歷問題，藉助於佇列來實現對二叉樹的層次遍歷 程式碼： import java.util.ArrayList;