迴歸問題就是擬合輸入變數x與數值型的目標變數y之間的關係，而線性迴歸就是假定了x和y之間的線性關係，公式如下：

　　如下圖所示，我們可以通過繪製繪製（x,y）的散點圖的方式來檢視x和y之間是否有線性關係，線性迴歸模型的目標是尋找一條穿過這些散點的直線，讓所有的點離直線的距離最短。這條完美直線所對應的引數就是我們要找的線性迴歸模型引數w1,w2,w3……b

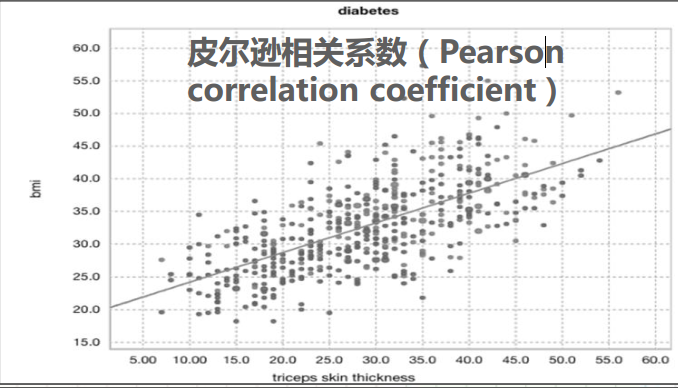
　　最小二乘法是一種求解迴歸模型引數w1,w2,w3……b的方法，線性迴歸模型中，能讓預測值和真實值誤差平方和最小的這條直線就是完美直線。

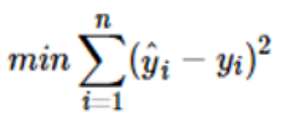
　　y^i表示第i個數據點的預測值，也就是對應完美直線的y值。最小二乘法通過求偏導數的方法讓誤差平方和取得最小值w1,w2,w3……b。

　　損失函式定義：

　　監督學習演算法的目標就是為了讓目標變數y的預測值和真實值儘量吻合，定義預測值與真實值之間的差異方法就叫損失函式。損失函式值越小，說明差異越小，模型的預測效果越好。線性迴歸中最小二乘法就是這個損失函式。

　　梯度下降法

　　在機器學習領域中，梯度下降法是更加通用的一種求解引數的方法。它的核心思想是 通過迭代逼近的方法尋找到讓損失函式取得最小值的引數，如下圖所示

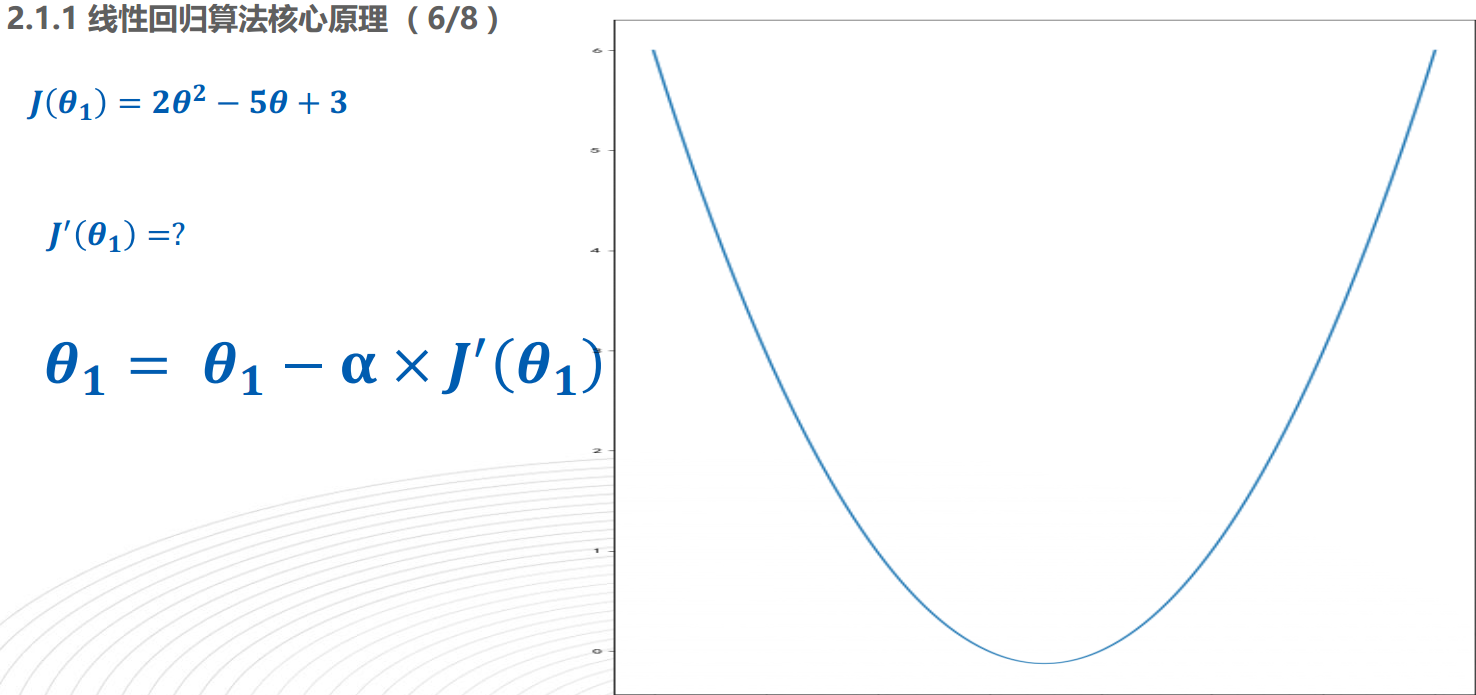
上圖中，J(ð)是損失函式，a是學習率，初始要設的小一點，這樣用梯度下降法時，才會更快的迭代到。迭代過程如下所示：

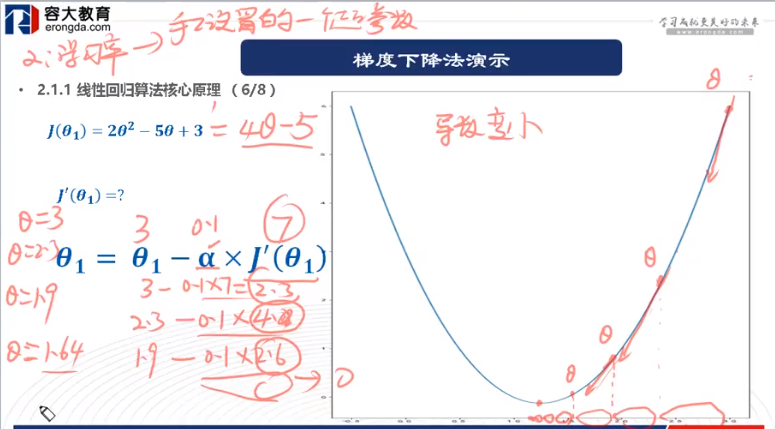
最終求出最合適的引數值