2. 程式人生 > >TensorFlow實戰——CNN（VGGNet19）——影象風格轉化

TensorFlow實戰——CNN（VGGNet19）——影象風格轉化

阿新 • • 發佈：2019-01-02

我們可以將一幅畫的風格提取，應用到兩外一幅畫中， 讓另一幅畫也擁有相同的畫風，

這樣我們就可以將我們喜歡的畫仿製為各種不同畫風的畫家的作品。

如何將一張花：


將其風格轉化為和梵高的《星夜》一樣具有鮮明藝術的風格呢？

這裡寫圖片描述

接下來我們來講解它。

影象資料

#定義命令引數
tf.app.flags.DEFINE_string('style_image','start.jpg','style image')
tf.app.flags.DEFINE_string('content_image','flow.jpg','content image')
tf.app.flags.DEFINE_integer('epochs'
 
,5000,'training epochs')
tf.app.flags.DEFINE_float('learning_rate',0.5,'learning rate')
FLAGS = tf.app.flags.FLAGS
if __name__ == '__main__': style = Image.open(FLAGS.style_image) style = np.array(style).astype(np.float32) - 128.0 content = Image.open(FLAGS.content_image) content = np.array(content).astype(np.float32) - 128.0
stylize(style,content,FLAGS.learning_rate,FLAGS.epochs)
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6

上述style讀取的是《星夜》，將其轉為浮點陣列，並且減去128.0，這樣就以0為中心，可以加快收斂。content讀取的是《西湖》，操作相同。

要注意的是，style，content圖片大小要相同。我在之前用“美圖秀秀”將《星夜》和《花》的大小轉為來224×224。

    print(content.shape)
    print(style.shape)
  • 1
  • 2

可見：

(224, 224, 3)
(224, 224, 3)
  • 1
  • 2

風格轉化

def stylize(style_image,content_image,learning_rate=0.1
 
,epochs=500):
    # 結果圖片
    target = tf.Variable(tf.random_normal(content_image.shape),dtype=tf.float32)
    style_input = tf.constant(style_image,dtype=tf.float32)
    content_input = tf.constant(content_image, dtype=tf.float32)
    cost = loss_function(style_input,content_input,target)
    train_op = tf.train.AdamOptimizer(learning_rate).minimize(cost)
    with tf.Session(config=tf.ConfigProto(log_device_placement=True)) as sess:
        tf.initialize_all_variables().run()
        for i in range(epochs):
            _,loss,target_image = sess.run([train_op,cost,target])
            print("iter:%d,loss:%.9f" % (i, loss))
            if (i+1) % 100 == 0:
                image = np.clip(target_image + 128,0,255).astype(np.uint8)
                Image.fromarray(image).save("./neural_me_%d.jpg" % (i + 1))
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15

這裡比較有趣的是，以前我們通常調優的是引數矩陣，然後配合測試資料預測出結果。而這邊，我們沒有測試資料，而所要調優的target矩陣，就是我們要得結果。

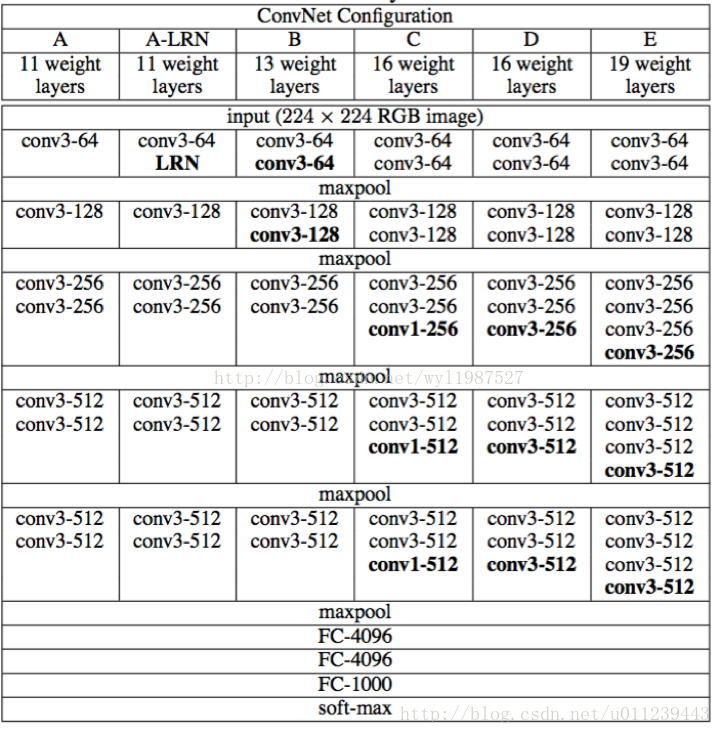
VGGNet19模型

VGGNet模型：

這裡寫圖片描述

然後只需要載入它據可以了：

_vgg_params = None

def vgg_params():
    global _vgg_params
    if _vgg_params is None:
        _vgg_params = sio.loadmat('imagenet-vgg-verydeep-19.mat')
    return _vgg_params
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
def vgg19(input_image):
    layers = (
        'conv1_1', 'relu1_1', 'conv1_2', 'relu1_2', 'pool1',
        'conv2_1', 'relu2_1', 'conv2_2', 'relu2_2', 'pool2',
        'conv3_1', 'relu3_1', 'conv3_2', 'relu3_2', 'conv3_3', 'relu3_3', 'conv3_4', 'relu3_4','pool3',
        'conv4_1', 'relu4_1', 'conv4_2', 'relu4_2', 'conv4_3', 'relu4_3', 'conv4_4', 'relu4_4', 'pool4',
        'conv5_1', 'relu5_1', 'conv5_2', 'relu5_2', 'conv5_3', 'relu5_3', 'conv5_4', 'relu5_4', 'pool5'
    )

    weights = vgg_params()['layers'][0]
    net = input_image
    network = {}
    for i,name in enumerate(layers):
        layer_type = name[:4]
        # 若是卷積層
        if layer_type == 'conv':
            kernels,bias = weights[i][0][0][0][0]
            # 由於 imagenet-vgg-verydeep-19.mat 中的引數矩陣和我們定義的長寬位置顛倒了，所以需要交換
            kernels = np.transpose(kernels,(1,0,2,3))
            conv = tf.nn.conv2d(net,tf.constant(kernels),strides=(1,1,1,1),padding='SAME',name=name)
            net = tf.nn.bias_add(conv,bias.reshape(-1))
            net = tf.nn.relu(net)
        # 若是池化層
        elif layer_type == 'pool':
            net = tf.nn.max_pool(net,ksize=(1,2,2,1),strides=(1,2,2,1),padding='SAME')
        # 將隱藏層加入到集合中
        # 若為`啟用函式`直接加入集合
        network[name] = net

    return network
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30

我們將weights打印出來看看：

print(weights.shape)
  • 1

得到：

(43,)
  • 1

可知imagenet-vgg-verydeep-19.mat還可以支援比VGGNet19更多層的VGGNet模型。

若是卷積層，如conv1_1：

print(weights[0][0][0][0][0])
  • 1

得到的是引數矩陣和偏置：

[ array([[[[ 0.39416704, -0.08419707, -0.03631314, ..., -0.10720515,
          -0.03804016,  0.04690642],
         [ 0.46418372,  0.03355668,  0.10245045, ..., -0.06945956,
          -0.04020201,  0.04048637],
         [ 0.34119523,  0.09563112,  0.0177449 , ..., -0.11436455,
          -0.05099866, -0.00299793]],

        [[ 0.37740308, -0.07876257, -0.04775979, ..., -0.11827433,
          -0.19008617, -0.01889699],
         [ 0.41810837,  0.05260524,  0.09755926, ..., -0.09385028,
          -0.20492788, -0.0573062 ],
         [ 0.33999205,  0.13363543,  0.02129423, ..., -0.13025227,
          -0.16508926, -0.06969624]],

        [[-0.04594866, -0.11583115, -0.14462094, ..., -0.12290562,
          -0.35782176, -0.27979308],
         [-0.04806903, -0.00658076, -0.02234544, ..., -0.0878844 ,
          -0.3915486 , -0.34632796],
         [-0.04484424,  0.06471398, -0.07631404, ..., -0.12629718,
          -0.29905206, -0.28253639]]],


       [[[ 0.2671299 , -0.07969447,  0.05988706, ..., -0.09225675,
           0.31764674,  0.42209673],
         [ 0.30511212,  0.05677647,  0.21688674, ..., -0.06828708,
           0.3440761 ,  0.44033417],
         [ 0.23215917,  0.13365699,  0.12134422, ..., -0.1063385 ,
           0.28406844,  0.35949969]],

        [[ 0.09986369, -0.06240906,  0.07442063, ..., -0.02214639,
           0.25912452,  0.42349899],
         [ 0.10385381,  0.08851637,  0.2392226 , ..., -0.01210995,
           0.27064082,  0.40848857],
         [ 0.08978214,  0.18505956,  0.15264879, ..., -0.04266965,
           0.25779948,  0.35873157]],

        [[-0.34100872, -0.13399366, -0.11510294, ..., -0.11911335,
          -0.23109646, -0.19202407],
         [-0.37314063, -0.00698938,  0.02153259, ..., -0.09827439,
          -0.2535741 , -0.25541356],
         [-0.30331427,  0.08002605, -0.03926321, ..., -0.12958746,
          -0.19778992, -0.21510386]]],


       [[[-0.07573577, -0.07806503, -0.03540679, ..., -0.1208065 ,
           0.20088433,  0.09790061],
         [-0.07646758,  0.03879711,  0.09974211, ..., -0.08732687,
           0.2247974 ,  0.10158388],
         [-0.07260918,  0.10084777,  0.01313597, ..., -0.12594968,
           0.14647409,  0.05009392]],

        [[-0.28034249, -0.07094654, -0.0387974 , ..., -0.08843154,
           0.18996507,  0.07766484],
         [-0.31070709,  0.06031388,  0.10412455, ..., -0.06832542,
           0.20279962,  0.05222717],
         [-0.246675  ,  0.1414054 ,  0.02605635, ..., -0.10128672,
           0.16340195,  0.02832468]],

        [[-0.41602272, -0.11491341, -0.14672887, ..., -0.13079506,
          -0.1379628 , -0.26588449],
         [-0.46453714, -0.00576723, -0.02660675, ..., -0.10017379,
          -0.15603794, -0.32566148],
         [-0.33683276,  0.06601517, -0.08144748, ..., -0.13460518,
          -0.1342358 , -0.27096185]]]], dtype=float32)
 array([[ 0.73017758,  0.06493629,  0.03428847,  0.8260386 ,  0.2578029 ,
         0.54867655, -0.01243854,  0.34789944,  0.55108708,  0.06297145,
         0.60699058,  0.26703122,  0.649414  ,  0.17073655,  0.47723091,
         0.38250586,  0.46373144,  0.21496128,  0.46911287,  0.23825859,
         0.47519219,  0.70606434,  0.27007523,  0.68552732,  0.03216552,
         0.60252881,  0.35034859,  0.446798  ,  0.77326518,  0.58191687,
         0.39083108,  1.75193536,  0.66117406,  0.30213955,  0.53059655,
         0.67737472,  0.33273223,  0.49127793,  0.26548928,  0.18805602,
         0.07412001,  1.10810876,  0.28224325,  0.86755145,  0.19422948,
         0.810332  ,  0.36062282,  0.50720042,  0.42472315,  0.49632648,
         0.15117475,  0.79454446,  0.33494323,  0.47283995,  0.41552398,
         0.08496041,  0.37947032,  0.60067391,  0.47174454,  0.81309211,
         0.45521152,  1.08920074,  0.47757268,  0.4072122 ]], dtype=float32)]
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45
  • 46
  • 47
  • 48
  • 49
  • 50
  • 51
  • 52
  • 53
  • 54
  • 55
  • 56
  • 57
  • 58
  • 59
  • 60
  • 61
  • 62
  • 63
  • 64
  • 65
  • 66
  • 67
  • 68
  • 69
  • 70
  • 71
  • 72
  • 73
  • 74
  • 75
  • 76
  • 77

若是啟用函式，如relu1_1：

print(weights[1][0][0][0][0])
  • 1

輸出：

relu
  • 1

若是池化層，如pool1：

print(weights[4][0][0][0][0])
  • 1

輸出：

pool1
  • 1

損失函式

STYLE_WEIGHT = 1
CONTENT_WEIGHT = 1
STYLE_LAYERS = ['relu1_2','relu2_2','relu3_2']
CONTENT_LAYERS = ['relu1_2']

def loss_function(style_image,content_image,target_image):
    style_features = vgg19([style_image])
    content_features = vgg19([content_image])
    target_features = vgg19([target_image])
    loss = 0.0
    for layer in CONTENT_LAYERS:
        loss += CONTENT_WEIGHT * content_loss(target_features[layer],content_features[layer])

    for layer in STYLE_LAYERS:
        loss += STYLE_WEIGHT * style_loss(target_features[layer],style_features[layer])

    return loss
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17

可以看到權重STYLE_WEIGHT和CONTENT_WEIGHT可以控制優化更 
取趨於風格還是趨於內容。而STYLE_LAYERS的層數越多，就能挖掘出《星夜》越多樣的風格特徵，而CONTENT_LAYERS中的越深的掩藏層得到的特徵越抽象。

建議STYLE_LAYERS中的層數儘可能的多，這樣更加能挖掘出《星夜》風格特徵。當然層數多了或者深了，所需要的迭代次數需要很大才能得到比較好的效果。迭代了500輪，只選了三個隱藏層'relu1_2','relu2_2','relu3_2'。而CONTENT_LAYERS中的隱藏層的越淺就表達了目標圖中原內容就越具像。

  • 內容損失函式很簡單，就是特徵值誤差：
def content_loss(target_features,content_features):
    _,height,width,channel = map(lambda i:i.value,content_features.get_shape())
    content_size = height * width * channel
    return tf.nn.l2_loss(target_features - content_features) / content_size
  • 1
  • 2
  • 3
  • 4
  • 風格損失函式。我們現將三維特徵矩陣(-1,channel)重塑為二維矩陣，即一行代表一個特徵值，三列分別是RGB。使用其格拉姆矩陣（ATA）誤差作為返回結果。
def style_loss(target_features,style_features):
    _,height,width,channel = map(lambda i:i.value,target_features.get_shape())
    size = height * width * channel
    target_features = tf.reshape(target_features,(-1,channel))
    target_gram = tf.matmul(tf.transpose(target_features),target_features) / size

    style_features = tf.reshape(style_features,(-1,channel))
    style_gram = tf.matmul(tf.transpose(style_features),style_features) / size

    return tf.nn.l2_loss(target_gram - style_gram) / size
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10

結果圖

好啦，接下來看看我們的作品吧。

迭代100輪：


迭代200輪：


迭代300輪：


迭代400輪：


迭代500輪：


可見結果圖的內容的原來越清晰的，但是過於清晰反而不具有藝術感，可以適當加深加多CONTENT_LAYERS中的隱藏層。注意圖片的右上部分，也可以發現越發具有類似於《星夜》的旋轉的風格紋路細節。

學習率會影響收斂的速度，內容的損失會和風格損失的係數會影響合成圖片的效果。特別來說，如果我們把內容損失的係數設定為0，也就是隻希望擬合風格圖的紋理，那麼我們只能得到《星空》

相關推薦

【轉載】TensorFlow實戰——CNN（VGGNet19）——影象風格轉化

轉自http://blog.csdn.net/u011239443/article/details/73721903 這次我們要做一件比較有趣的事——講影象風格轉化。 如何將一張杭州西湖圖片： 將其風格轉化為和梵高的《星夜》一樣具有鮮明藝術的風格呢？ 先給出完整的

TensorFlow實戰——CNN（VGGNet19）——影象風格轉化

我們可以將一幅畫的風格提取，應用到兩外一幅畫中， 讓另一幅畫也擁有相同的畫風， 這樣我們就可以將我們喜歡的畫仿製為各種不同畫風的畫家的作品。 如何將一張花： 將其風格轉化為和梵高的《星夜》一樣具有鮮明藝術的風格呢？ 接下來我們來講解它。 影象資料 #定

TensorFlow實戰——CNN（LeNet5）——MNIST數字識別

train 首先，原始學習率要降低： LEARNING_RATE_BASE = 0.01 第二點，x是一個四維的矩陣： x = tf.placeholder(tf.float32,[BA

深度學習tensorflow實戰筆記（5）用預訓練好的VGG-16模型提取影象特徵

     上一篇部落格介紹瞭如果使用自己訓練好的模型用於影象分類和特徵提取，但是有時候自己的資料集大小有限，所以更多的時候我們需要用VGG-16預訓練好的模型提取特徵，相關學者預訓練好的模型使用的都是公開的標準資料集，所以我們直接用預訓練的模型提取我們自己影象的特徵，可以用於

TensorFlow實戰筆記（17）---TFlearn

目錄： 分散式Estimator 自定義模型 建立自己的機器學習Estimator 調節RunConfig執行時的引數 Experiment和LearnRunner 深度學習Estimator 深度神經網路 廣度深度模型

卷積神經網路CNN（1）——影象卷積與反捲積（後卷積，轉置卷積）

1.前言    傳統的CNN網路只能給出影象的LABLE，但是在很多情況下需要對識別的物體進行分割實現end to end，然後FCN出現了，給物體分割提供了一個非常重要的解決思路，其核心就是卷積與反捲積，所以這裡就詳細解釋卷積與反捲積。     對於1維的卷積，公式（離散

深度學習tensorflow實戰筆記（3）VGG-16訓練自己的資料並測試和儲存模型

    前面的部落格介紹瞭如何把影象資料轉換成tfrecords格式並讀取，本篇部落格介紹如何用自己的tfrecords格式的資料訓練CNN模型，採用的模型是VGG-16。現有的教程都是在mnist或者cifar-10資料集上做的訓練，如何用自己的資料集進行訓練相關的資料比較

深度學習tensorflow實戰筆記（1）全連線神經網路（FCN）訓練自己的資料（從txt檔案中讀取）

      寫在前面的話：離上一次寫部落格已經有些日子了，以前的工程都是在caffe平臺下做的，caffe平臺雖然挺好用的，但是caffe主要用於做CNN，對於其它的網路模型用起來不太方便，所以博主轉戰tensorflow，Google對待tensorflow就想當年對待An

基於PyTorch的深度學習入門教程（八）——影象風格遷移

前言 本文介紹怎樣執行Neural-Style演算法。Neural-Style或者叫做Neural-Transfer，將一個內容影象和一個風格影象作為輸入，返回一個按照所選擇的風格影象加工的內容影象。 原理是非常簡單的：我們定義兩個距離，一個用於內容（Dc）

深度學習tensorflow實戰筆記（4）利用儲存的VGG-16CNN網路模型提取特徵

    前幾篇部落格寫了如何處理資料，如何把用自己的資料訓練VGG-16，如何把訓練好的模型儲存。而在實際應用中，並不是所有的操作都是為了分類的，有時候需要提取影象的特徵，那麼怎麼利用已經儲存的模型提取特徵呢？   “桃葉兒尖上尖，柳葉兒就遮滿了天”    測試資料轉換成tf

羅斯基白話：TensorFlow+實戰系列（四）變數管理

白話TensorFlow +實戰系列（一）變數管理        這篇文章主要記錄常用的兩種管理變數的方法。個人感覺變數管理是比較重要的，特別是當建立一個複雜的神經網路的時候，變數一旦增多，如果不

機器學習筆記（十二）：TensorFlow實戰四（影象識別與卷積神經網路）

1 - 卷積神經網路常用結構 1.1 - 卷積層 我們先來介紹卷積層的結構以及其前向傳播的演算法。 一個卷積層模組，包含以下幾個子模組： 使用0擴充邊界(padding) 卷積視窗過濾器（filter） 前向卷積 反向卷積（可選） 1.1

機器學習筆記（十八）：TensorFlow實戰十（影象資料處理）

1 - 引言 之前我們介紹了通過卷積神經網路可以給影象識別技術帶來突破性的進展，現在我們從影象的預處理這個角度來繼續提升我們影象識別的準確率。 輸入的預處理需要使用TFRecord格式來同一不同的原始資料格式，並且更加有效的管理不同的屬性。 並且TensorFlow支援影象處理函式，

TensorFlow：實戰Google深度學習框架（五）影象識別與卷積神經網路

第6章 影象識別與卷積神經網路 本章通過利用CNN實現影象識別的應用來說明如何使用TensorFlow實現卷積神經網路 6.1 影象識別問題簡介及經典資料集 1. Cifar Cifar-10：10種不同種類的60000張影象，畫素大小為3

TensorFlow 實戰（五）—— 影象預處理

當然 tensorflow 並不是一種用於影象處理的框架，這裡影象處理僅僅是一些簡單的畫素級操作，最終目的比如用於資料增強； tf.random_crop() tf.image.random_fli

TensorFlow框架實戰學習（1）

msu HA gin PE var shape highlight padding lin 1 import tensorflow as tf 2 import numpy as np 3 import matplotlib.pyplot as plt 4

機器學習筆記（十一）： TensorFlow實戰三（MNIST數字識別問題）

1 - MNIST數字識別問題 前面介紹了這樣用TensorFlow訓練一個神經網路模型和主要考慮的問題及解決這些問題的常用方法。下面我們用一個實際的問題來驗證之前的解決方法。 我們使用的是MNIST手寫數字識別資料集。在很多深度學習教程中，這個資料集都會被當做一個案例。 1.1

機器學習筆記（十）：TensorFlow實戰二（深層神經網路）

1 - 深度學習與深層神經網路 深度學習的精確定義為：“一類通過多層非線性變換對高複雜性資料建模演算法的集合” 因此，多層神經網路有著2個非常重要的特性 多層 非線性 1.1 - 線性模型的侷限性 線上性模型中，模型的輸出為輸入的加權和，假設一

機器學習筆記（九）：Tensorflow 實戰一 （Tensorflow入門）

1 - TsensorFlow計算模型 ——計算圖 1.1- 計算圖的概念 計算圖是TensorFlow中最基本的一個概念，TensorFlow中的所有計算都會被轉化為計算圖上的節點。 在TensorFlow中，張量可以簡單地理解為多為陣列。如果說TensorFlow的第一個詞T

機器學習筆記（十五）：TensorFlow實戰七（經典卷積神經網路：VGG）

1 - 引言 之前我們介紹了LeNet-5和AlexNet，在AlexNet發明之後，卷積神經網路的層數開始越來越複雜，VGG-16就是一個相對前面2個經典卷積神經網路模型層數明顯更多了。 VGGNet是牛津大學計算機視覺組（Visual Geometry Group）和Google