內容都是是演算法導論上的，僅作為一個閱讀筆記，記錄一下自己閱讀過程中碰到的一些問題。希望能對需要的同學有所幫助！

矩陣鏈乘法是指給定一個n個矩陣的序列（矩陣鏈）< A1, A2, …, An>，我們希望計算它們的乘積

A1A2A3…An

對於這個問題，我們可以先用括號明確計算的次序，然後利用標準的矩陣相乘演算法進行計算。由於矩陣乘法滿足結合律，所以任何加括號的方法都會得到相同的計算結果。

1、矩陣鏈的完全括號化

如果矩陣鏈是單一矩陣（即只有一個矩陣），或者是兩個完全括號化的矩陣乘積鏈的積，且已外加括號，那麼這個矩陣鏈是完全括號化的。

例如，如果矩陣鏈為< A1, A2, A3, A4>，則共有5種完全括號化的矩陣乘積鏈：

(A1(A2(A3A4)))
(A1((A2A3)A4))
((A1A2)(A3A4))
((A1(A2A3))A4)
(((A1A2)A3)A4)

因為對矩陣鏈加括號的方式不同會對乘積運算的代價產生巨大影響，所以用找出一種最好的加括號方式來減少運算量。

2、矩陣鏈乘法問題

矩陣鏈乘法問題可以描述為：給定n個矩陣的鏈< A1, A2, …, An>，矩陣A_i的規模為p_i-1×P_i，求完全括號化方案，使得計算乘積A1A2…An所需的乘法次數最少。

注意：求解矩陣鏈乘法問題並不是要真正進行矩陣相乘運算，我們的目標只是確定代價最小的運算順序

3、有多少括號化方案

我們可以先來確定一下有多少括號化方案。對一個n個矩陣的鏈，令P(n)表示可供選擇的括號化方案的數量。當n=1時，由於只有一個矩陣，因此只有一種完全括號化方案。當n>=2時，完全括號化的矩陣乘積可描述為兩個完全括號化的部分積相乘的形式，而兩個部分積的劃分點在第k個矩陣和第k+1個矩陣之間，k為1, 2, …, n-1中的任意一個值。因此可得到如下遞迴公式：

P(n)=1,當n=1時

P(n)=ΣP(k)P(n-k), n>1時,其中k為1, 2, …, n-1

注意：P(n)=ΣP(k)P(n-k)的由來。假定我們現在選的分割點是k，則分割點前面有k個矩陣且有P(k)種括號化的方案，後面有n-k個矩陣且有P(n-k)種括號化的方案，因此當分割點為k時總共有P(k)P(n-k)種括號化方案。而k的取值範圍為1, 2, …, n-1，所以總的括號化的方案數 就是k的各個取值時的括號化方案數求和。

4、應用動態規劃方法

（1）最優化方案的結構特徵

動態規劃方法的第一步是尋找最優子結構，然後利用這種子結構從子問題的最優解構造出原問題的最優解。在矩陣鏈乘法問題中，我們用符號A_i…j(i<=j)表示A_iA_i+1…A_j乘積的結果矩陣。可以看出，如果i < j那麼為了對A_iA_i+1…A_j進行括號化，我們就必須在某個A_k和A_k+1之間將矩陣鏈劃分開（k為i<=k< j間的整數）。也就是說，我們首先計算矩陣A_i..k和A_k+1..j，然後再計算它們的乘積得到最終結果A_i..j。此方案的計算代價等於矩陣A_i..k的計算代價，加上矩陣A_k+1..j的計算代價，再加上兩者相乘的計算代價。

本問題的最優子結構：假設A_iA_i+1…A_j的最優括號化方案的分割點在A_k和A_k+1之間。那麼在對“字首”子鏈A_iA_i+1…A_k進行括號化時，我們採用它的最優方案。對子鏈A_k+1A_k+2…A_j我們也採用它的最優化方案。

如不理解請看《演算法導論》

我們可以看到，一個長度大於1的矩陣鏈乘法問題的任何解都需要對它進行劃分，而任何最優解都是由子問題的最優解構成的。因此，為了構造一個矩陣鏈乘法的最優解，我們可以將問題劃分為兩個子問題（A_iA_i+1…A_k和A_k+1A_k+2…A_j的最優化括號化問題），求出子問題的最優解，然後將子問題的最優解組合起來。同時我們必須考察所有可能的劃分點，保證不會遺漏最優解。

（2）一個遞迴求解方案

我們可以用子問題的最優解來遞迴地定義原問題最優解的代價。我們可以將對所有1<=i<=j<=n確定A_iA_i+1…A_j的最小代價括號化方案作為子問題。令m[i] [j]表示計算矩陣A_i..j所需乘法次數的最小值，那麼，原問題的最優解——計算A_i..n所需的最低代價就是m[1] [n]。

遞迴定義m[i][j]如下。對於i=j時的平凡問題，矩陣鏈只包含唯一的矩陣A_i..i=A_i，因此不需要任何乘法運算。所以，對所有i=1, 2, …, n，m[i][i]=0。若i< j，我們利用（1）中的最優子結構（即最優解）來計算m[i] [j]。我們假設A_iA_i+1…A_j的最優化括號化方案的分割點在矩陣A_k和A_k+1之間，其中i<=k< j。那麼m[i][j]就等於計算A_i..k和A_k+1..j的代價加上兩者乘積的代價的最小值。由於矩陣A_i的大小為p_i-1×p_i，易知A_i..k和A_k+1..j相乘的代價為p_i-1p_kp_j次乘法運算。因此，我們得到

m[i][j]=m[i][k]+m[k+1][j]+p_i-1p_kp_j

此遞迴公式中的最優分割點k是已知的，但實際上我們不知道，所以需要在i和j之間檢查k的每一種可能，找出最優的那個k值。

m[i][j]=0, 如果i=j
m[i][j]=min{m[i][k]+m[k+1][j]+p_i-1p_kp_j},其中k=i,i+1,.. j-1 如果i< j

m[i][j]的值給出了子問題最優解的代價，但它並未提供足夠的資訊來構造最優解。因此，我們用s[i][j]儲存A_iA_i+1…A_j最優括號化方案的分割點位置k，也就是使m[i][j]=m[i][k]+m[k+1][j]+p_i-1p_kp_j成立的k值。

（3）計算最優代價

此遞迴演算法使指數時間的，並不比檢查所有括號化方案的暴力搜尋方法更好。同時可以注意到，我們需求解的不同子問題數目使相對比較少的：每對滿足1<=i<=j<=n的i和j對應一個唯一的子問題，共有C_n²+n=O(n²)個。遞迴演算法會在遞迴呼叫樹的不同分支中多次遇到同一個子問題。這種子問題重疊的性質是應用動態規劃的另一個標識（第一個標識是最優子結構）。

不同子問題數目的確定：當i=j時，共有n個子問題；當i< j時，相當於在n個數中任取2個的組合數（把取出的2個數中較小的數賦給i,大的賦給j），是C_n²，所以總數是C_n²+n。

我們採用自底向上的表格法代替遞迴法。
虛擬碼如下：

MATRIX-CHAIN-ORDER(p)
    n=p.length-1
    let m[1..n][1..n] and s[1..n-1][2..n] be new tables
    for i=1 to n
        m[i][i]=0 // 也就是把二維陣列m中主對角線元素置為0
    for l=2 to n   // l is the chain lenth(即 2個矩陣相乘，3個相乘，...n個相乘)
        for i=1 to n-l+1 // 控制行的變換，可以把陣列m在紙上畫出來，發現i是控制對角線上的行變換。
            j=i+l-1 //即j=i+(l-1)， 本來主對角線上是j=i的，但是，當矩陣鏈為l時，列(即j）右移（l-1）位，所以j=i+(l-1)，也就是控制列的變化
            m[i][j]=∞
            for k=i to j-1
                q=m[i] [k]+m[k+1] [j]+p[i-1]p[k]p[j]
                if q< m[i][j]
                    m[i][j]=q
                    s[i][j]=k
    return m and s

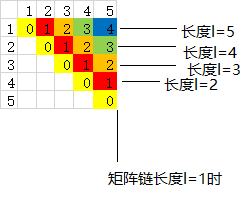
自底向上方法：以A1A2A3A4A5矩陣鏈為例，長度為1的矩陣鏈的乘法次數為0，填充主對角線上的元素為0；長度為2的矩陣鏈，即2個矩陣相乘時，填充的是主對角線右上方的對角線元素。換句話說就是：長度為1時，計算的結果是m[1][1],m[2][2],m[3][3],m[4][4],m[5][5]，即二維陣列m中的主對角線元素。長度為2時，計算結果是m[1][2],m[2][3],m[3][4],m[4][5]。長度為3時也類似。所以i=1 to n-l+1和j=i+l-1 //即j=i+(l-1)也就很好理解了。