七月演算法4月機器學習演算法班課程筆記——No.10

前言

　　與迴歸與分類不同，聚類是無監督學習演算法，無監督指的是隻需要資料，不需要標記結果，試圖探索和發現一些模式。比如對使用者購買模式的分析、影象顏色分割等。聚類演算法的提出比較早，是資料探勘的一個重要模組，可以對大量資料分類並概括出每一類的特點。目前也有很多種聚類演算法，包括劃分法、層次法、基於密度的方法、基於網格的方法等。實際生產中，很少有隻用聚類演算法的系統，因為聚類效果的好壞不容易衡量，有時候會用做監督學習中稀疏特徵的預處理。
　　接下來會重點介紹K-means聚類、層次聚類和混合高斯模型。

1. 聚類演算法思想

　　聚類演算法的思想：給定N個訓練樣本(未標記的)x1,x2,...,xN，目標是把比較“接近” 的樣本放到一個cluster裡， 總共得到K個cluster。沒有給定標記，聚類唯一會使用到的資訊是樣本與樣本之間的相似度，聚類就是根據樣本相互之間的相似度“抱團” 的。那麼怎麼評定聚類的好壞呢？——也是用相似度評定，會盡量希望“ 高類內相似度， 低類間相似度”。
　　評定內容的選擇：相似度評定對於聚類至關重要，選用的評定內容決定了相似度的偏向。看下面的兩張圖：
　　
　　如果以輪廓和色調作為評定標準，那麼這兩張圖很容易被分為一類，如果以眼睛鼻子來評定，就能區分開。所以在不同的場景下，應該選用不同的評定內容。例如：
　　- 圖片檢索： 圖片內容相似度
　　- 圖片分割： 圖片畫素(顏色)相似度
　　- 網頁聚類： 文字內容相似度
　　- 社交網路聚類： (被)關注人群， 喜好， 喜好內容
　　- 電商使用者聚類： 點選/加車/購買商品， 行為序列。比如按時間聚類，夜晚12點以後還在購物的多是學生黨。
　　計算相似度距離

：不管用什麼樣的評定內容，最終都會把樣本表示成向量，那麼向量的距離怎麼表示呢？常用的距離計算公式有：
　　- 歐式距離
　　

d(x,z)=∥x−z∥=∑d=1D(xd−zd)2−−−−−−−−−−−⎷
　　- 曼哈頓距離
　　d(x,z)=∑d=1D|xd−zd|
　　- 餘弦距離：保證不了迭代的收斂，中心距離不像歐式距離簡單直觀。
　　- 核函式對映後距離
　　d(x,z)=∥ϕ(x)−ϕ(z)∥
　　接下來細講的三個演算法中，K-means， 高斯混合模型是一個獨立於另外一個的，需要輸入聚類個數；層次聚類可以看做樹狀層疊，無需初始輸入聚類個數。

2. K-means聚類

2.1 K-means聚類演算法

　　K-means是提出非常早， 使用非常頻繁的聚類演算法。之前面試的時候我以為面試官會問比較難的聚類演算法，但是發現多是問k-means，不過不僅僅是描述演算法，要知道k-means的優缺點、適用場合，會問一些細緻的問題。現在理解為什麼了，因為公司大多也不會用太複雜的演算法，K-means算是聚類中用的最多的了。

輸入：N個樣本、擬定的聚類個數K
初始化：隨機初始化K個D維的向量 或 選取K個不同的樣本點作為初始聚類中心
迭代直至收斂：
1. 對於每個樣本xn都指定其為離其最近的聚類中心的cluster
2. 重新計算聚類中心

　　迭代收斂怎麼定義呢？ 一是聚類中心不再有變化，二是每個樣本到對應聚類中心的距離之和不再有很大變化。
　　下面演示聚類的過程。
　　初始化：比如以下樣本點要聚成2類，先隨機初始化兩個中心點。
　　
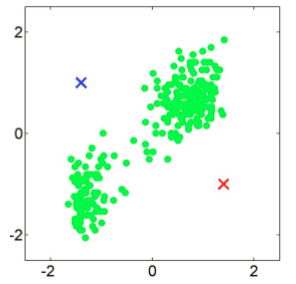
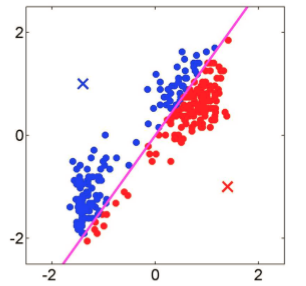
　　計算距離，分類：對原始資料中的每個樣本點，分別計算到兩個中心點的距離，樣本點離哪個中心的距離近，就分到相應的類別中。如下圖，得到兩個類別的分隔線，其實這條線也可以是兩個點的垂直平分線，因為垂直平分線的性質可知，垂直平分線上的點，到兩個中心點的距離相同。
　　
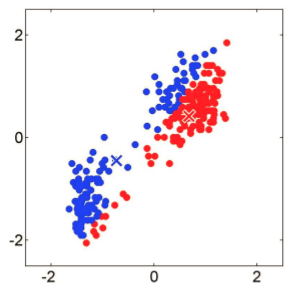
　　重新計算中心點：把藍色點的位置的平均值作為藍色的中心點，同理紅色。
　　
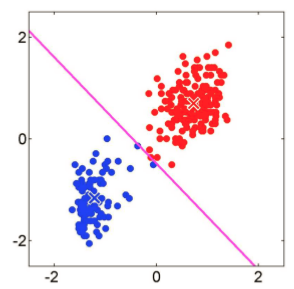
　　迭代：重新計算距離分類，重新計算中心點，知道達到了收斂條件。
　　
　　

2.2 初始化中心的選擇

　　K-means演算法確實是對初始化聚類中心敏感的，比較好的初始中心不僅可以降低迭代次數，也會引導更好的聚類結果。上面提到，初始化中心是隨機產生的，那麼怎麼優化初始化中心呢？
　　1. 初始第一個聚類中心為某個樣本點， 初始第二個聚類中心為離它最遠的點， 第三個為離它倆最遠的。
　　2. 多初始化幾遍， 選所有這些聚類中損失函式(到聚類中心和)最小的。其中損失函式的定義如下。假定μ1,...,μk為k個聚類中心，用rnk∈0,1表示xn是否屬於聚類k，則損失函式的散度（混亂度）為：
　　

J(μ,r)=∑n=1N∑k=1Krnk∥xn−μk∥2
　　3. 使用優化的初始化聚類方法。例如Arthur 和 Vassilvitskii 提出的Kmeans++，會找最遠的一些點初始化。

2.3 K值的選擇

　　k-means的輸入需要知道聚類個數，對於大量的資料，我們如何知道應該分為幾類合理呢？而且k值選的不好確實會出現下面的狀況，例如資料實際上劃分為2類比較合理，如果硬性的劃分為1類，或者3類，就沒有很好的效果。
　　
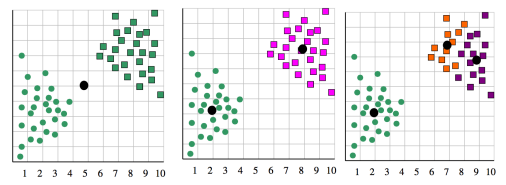
　　選擇方法：“肘點” 法。選取不同的K值，畫出損失函式曲線。
　　
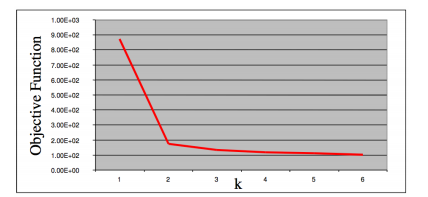
　　這裡分析之後可以取k=2，因為2之後的損失函式變化不大。肘點法是教科書上經常介紹的方法，但是實際工作中，肘點法卻不見得好用。

【實際案例】：有80w個商品的圖片，希望實現聚類，每100個數據為一類。
   直觀思路：80w/100,約為8000個類，然後設定k=8000，把畫素值展開跑實驗，沒有優化預設跑十遍，
實驗資料要跑兩三天。
   優化思路：把商家的文字描述，比如顏色，長短等，先按文字聚200個類，然後並行的對這200各類按
照上述方式實驗，三個小時可以完成。
   聚類個數k怎麼定呢？肘點法太耗時了。建議先定估計一個值，聚類後觀察每個簇的元素個數，若有一些
簇元素很少，考慮降低k，如果比較平均，在考慮增加k。若某個簇元素個數很多，可以考慮單
獨對這個簇再聚類。
   嗯，這也是海量資料數理的常用方法——分治法。

　　下圖表示了不同的K取值對影象分割的影響（聚類很多時候也是業務相關的）。
　　

2.4 K-means侷限性

　　1. 屬於“硬聚類” ， 每個樣本只能有一個類別。 其他的一些聚類方法(GMM或者模糊K-means允許“軟聚類”)。
　　2. K-means對異常點的“免疫力” 很差， 我們可以通過一些調整，比如中心不直接取均值， 而是找均值最近的樣本點代替——k-medoids演算法。
　　3. 對於團狀的資料點集區分度好， 對於帶狀(環繞)等“非凸”形狀不太好。 (用譜聚類或者做特徵對映)

3. 層次聚類

　　K-means裡面的K太難確定了，有的同學會有疑惑“無監督的聚類還需要指定k呀？有沒有不需要指定k的聚類呢？“，下面來看看層次聚類。層次聚類是教科書上必講的內容，比較容易理解，層次聚類就是通過對資料集按照某種方法進行層次分解，直到滿足某種條件為止。按照分類原理的不同，可以分為凝聚和分裂兩種方法。
　　凝聚型：比如有五個樣本，先把每一個樣本看做一簇，然後選擇最近的兩個樣本歸為一簇，得到4個簇，然後4個簇中選兩個最近的簇作為一簇，直到所有的樣本聚在一起就停止。可以想象整個過程會很慢。
　　
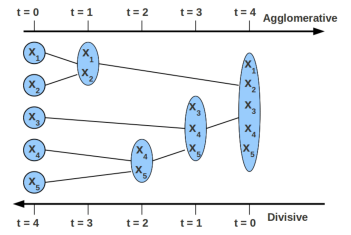
　　演算法中比較重要的是計算cluster R和cluster S之間的距離，介紹三種方法：
　　
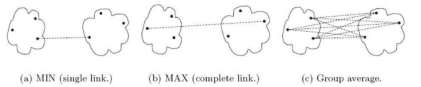
　　1. 最小連線距離法
　　

d(R,S)=minxR∈R,xS∈Sd(xR,xS)
　　2. 最大連線距離法
　　d(R,S)=maxxR∈R,xS∈Sd(xR,xS)
　　3. 平均連線距離法
　　d(R,S)=1|R∥S|∑xR∈R,xS∈Sd(xR,xS)
　　雖然慢，但是還是有好處的，比如生物上基因工程應用廣泛，因為可以得到每個粒度的情況。
　　K-means VS 層次聚類？
　　1. K-means這種扁平聚類產出一個聚類結果(都是獨立的)
　　2. 層次聚類能夠根據你的聚類程度不同，有不同的結果
　　3. K-means需要指定聚類個數K，層次聚類不用
　　4. K-means比層次聚類要快一些(通常說來)
　　5. K-means用的多
　　

4. 混合高斯模型(GMM)

　　高斯模型，給定均值和方差，將一個事物分解為基於高斯概率密度函式（正態分佈曲線）形成的模型。
　　

P(x)=φ(x;μ,σ)=1σ2π−−√exp(−(x−μ)22σ2)
　　
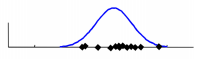
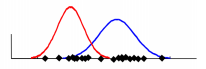
　　但是有時候不是隻有一個密集區域，而是多個密集區域，需要多個高斯模型線性加權而成。高斯混合模型就是用高斯概率密度函式（正態分佈曲線）精確地量化事物，它是一個將事物分解為若干的基於高斯概率密度函式形成的模型。
　　P(C=i)=ωi,P(x|C=i)=φ(x;μi,σi)P(x)=∑

相關推薦

聚類演算法與應用

七月演算法4月機器學習演算法班課程筆記——No.10 前言 　　與迴歸與分類不同，聚類是無監督學習演算法，無監督指的是隻需要資料，不需要標記結果，試圖探索和發現一些模式。比如對使用者購買模式的分析、影象顏色分割等。聚類演算法的提出比較早，是資料探勘的一

k-means聚類演算法與區域性最優解

1 演算法概述 1.1 無監督學習 本章演算法區別於之前的機器學習演算法，因為k-means演算法屬於無監督演算法。監督學習的意思是所給的訓練資料都帶有標籤，如類別等，我們在訓練演算法時，要考慮預測的

scikit-learn學習之K-means聚類演算法與 Mini Batch K-Means演算法

======================================================================本系列部落格主要參考 Scikit-Learn 官方網站上的每一個演算法進行，並進行部分翻譯，如有錯誤，請大家指正    轉載請註明出

Canopy聚類演算法與Mahout中的實現

前面提到的kmeans 演算法需要提前設定簇的個數，我們也可以根據資料進行簡單簇數目估計，但是有一類稱為近似聚類演算法技術可以根據給定資料集估計簇的數量以及近似的中心位置，其中有一個典型演算法就是canopy生成演算法。 Mahout中kmeans 演算法實現使用Rando

scikit-learn學習之K-means聚類演算法與 Mini Batch K-Means演算法 [轉自別的作者，還有其他sklearn翻譯]

http://blog.csdn.net/gamer_gyt/article/details/51244850 ====================================================================== 本系列部落格主要

模式識別：C-means(K-means)聚類演算法與分級聚類(層次聚類)演算法

  C均值聚類演算法與分級聚類演算法的聚類分析 一、實驗目的 理解聚類的整體思想，瞭解聚類的一般方法； 掌握 C-means與分級聚類演算法演算法思想及原理，並能夠熟練運用這些演算法進行聚類分析； 能夠分析二者的優缺點 二、實驗內容 採用C均

Thinking in SQL系列之五：資料探勘K均值聚類演算法與城市分級

原創： 牛超   2017-02-21   Mail：[email protected] 引言：前一篇文章開始不再介紹簡單演算法，而是轉到資料探勘之旅。感謝CSDN將我前一篇機器學習C4.5決策樹演算法的博文推送到了首頁，也非常榮幸能夠得到雲和恩墨的蓋老師的

基礎演算法（二）：Kmeans聚類演算法的基本原理與應用

Kmeans聚類演算法的基本原理與應用       內容說明：主要介紹Kmeans聚類演算法的數學原理，並使用matlab程式設計實現Kmeans的簡單應用，不對之處還望指正。 一、Km

K-means聚類演算法原理分析與實際應用案例分析（案例分析另起一篇部落格）

引言 在資料分析中，我們常常想將看上去相似或者行為形似的資料聚合在一起。例如，對一個營銷組織來說，將不同客戶根據他們的特點進行分組，從而有針對性地定製營銷活動，這很重要。又比如，對學校老師來說，將學生分組同樣能夠有所側重的進行教育活動。分類與聚類是資料探勘領域

聚類演算法—K-Means原理與應用

聚類演算法是一類非監督學習的演算法，在給定的一個數據集中，給了N個樣本，沒有給出樣本對應的標籤類別資料y，可以利用聚類演算法，進行標籤的分類。 K-Means演算法的原理與步驟： 1>   在N個樣本總體中，隨機抽出k個初始資料的質心，接著把資料集中的樣本取出，計算

聚類演算法之DBSCAN演算法之二：高維資料剪枝應用NQ-DBSCAN

一、經典DBSCAN的不足 1.由於“維度災難”問題，應用高維資料效果不佳 2.執行時間在尋找每個點的最近鄰和密度計算，複雜度是O(n2)。當d>=3時，由於BCP等數學問題出現，時間複雜度會急劇上升到Ω（n的四分之三次方）。 二、DBSCAN在高維資料的改進 目前的研究有

結合Doc2Vec與改進聚類演算法的中文單文件自動摘要方法研究

                                                                      圖1 本文方法示意圖 一．基於Doc2Vec 的句子向量訓練        Doc2Vec 模型能很好地結合上下文語境, 挖

K-means均值聚類演算法的原理與實現

轉自：http://blog.csdn.net/xiaolewennofollow/article/details/45541159 K-均值聚類演算法的原理與實現 聚類是一種無監督的學習，它將相似的物件歸到同一個簇中，聚類方法幾乎可以應用於所有物件，簇內的物件越相似，聚類的效果越好，本文主要介紹K-均值聚

機器學習聚類演算法Kmeans與DBSCAN

自己對兩種聚類方法的一點理解。1. KMeans1.1 演算法概述Kmeans是一種劃分聚類的方法，基本K-Means演算法的思想很簡單，事先確定常數K，常數K意味著最終的聚類類別數，首先隨機選定初始點為質心，並通過計算每一個樣本與質心之間的相似度(這裡為歐式距離)，將樣本點

視覺SLAM之詞袋（bag of words） 模型與K-means聚類演算法淺析（1）

第一步：利用SIFT演算法從不同類別的影象中提取視覺詞彙向量，這些向量代表的是影象中區域性不變的特徵點； 第二步：將所有特徵點向量集合到一塊，利用K-Means演算法合併詞義相近的視覺詞彙，構造一個包含K個詞彙的單詞表； 第三步：統計單詞表中每個單詞在影象中出現的次數，從而將影象表示成為一個K維數值向量。

聚類演算法之K-means演算法與聚類演算法衡量指標

聚類就是按照某個特定標準(如距離準則)把一個數據集分割成不同的類或簇，使得同一個簇內的資料物件的相似性儘可能大，同時不在同一個簇中的資料物件的差異性也儘可能地大。即聚類後同一類的資料儘可能聚集到一起

【R與聚類演算法】：確定K值個數

在無監督學習中，很多朋友都會面臨同一個問題，我們應該將使用者聚成幾類？即如何確定K值問題。下面我們介紹兩種常用的方法。輪廓係數法Nbcluster輪廓係數法    首先，我們載入資料，並對資料進行預先處理。請看

聚類演算法應用場景例項十則

       本文整理了10個天池、DataCastle、DataFountain等中出現的，可使用聚類演算法處理的問題場景例項。 1 基於使用者位置資訊的商業選址         隨著資訊科技的快速發展，移動裝置和移動網際網路已經普及到千家萬戶。在使用者使用行動網路時

K-means聚類演算法的三種改進(K-means++,ISODATA,Kernel K-means)介紹與對比

  一、概述       在本篇文章中將對四種聚類演算法(K-means,K-means++,ISODATA和Kernel K-means)進行詳細介紹，並利用資料集來真實地反映這四種演算法之間的區別。       首先需要明確的是上述四種演算法都屬於"硬聚類”演算法，即資料集中每一個樣本都是被100%確定得

模糊聚類演算法（FCM）和硬聚類演算法（HCM)的VB6.0實現及其應用

Private Function Fcm(ByRef Data() As Double, ByVal Cluster As Long, Optional ByVal CreateIniCenter As IniCenterMethod = IniCenterMethod.CreateByHcm, Option