一、概述

      在本篇文章中將對四種聚類演算法(K-means,K-means++,ISODATA和Kernel K-means)進行詳細介紹，並利用資料集來真實地反映這四種演算法之間的區別。

      首先需要明確的是上述四種演算法都屬於"硬聚類”演算法，即資料集中每一個樣本都是被100%確定得分到某一個類別中。與之相對的"軟聚類”可以理解為每個樣本是以一定的概率被分到某一個類別中。

      先簡要闡述下上述四種演算法之間的關係，已經瞭解過經典K-means演算法的讀者應該會有所體會。沒有了解過K-means的讀者可以先看下面的經典K-means演算法介紹再回來看這部分。

     (1)

      (2) K-means與ISODATA：ISODATA的全稱是迭代自組織資料分析法。在K-means中，K的值需要預先人為地確定，並且在整個演算法過程中無法更改。而當遇到高維度、海量的資料集時，人們往往很難準確地估計出K的大小。ISODATA就是針對這個問題進行了改進，它的思想也很直觀：當屬於某個類別的樣本數過少時把這個類別去除，當屬於某個類別的樣本數過多、分散程度較大時把這個類別分為兩個子類別。

      (3) K-means與Kernel K-means：傳統K-means採用歐式距離進行樣本間的相似度度量，顯然並不是所有的資料集都適用於這種度量方式。參照支援向量機中核函式的思想，將所有樣本對映到另外一個特徵空間中再進行聚類，就有可能改善聚類效果。本文不對Kernel K-means進行詳細介紹。

      可以看到，上述三種針對K-means的改進分別是從不同的角度出發的，因此都非常具有代表意義。目前應用廣泛的應該還是K-means++演算法（例如2016年底的NIPS上也有針對K-means++的改進，感興趣的讀者可以進一步學習）。

二、經典K-means演算法

演算法描述如下，非常清晰易懂。經典K-means演算法應該是每個無監督學習教程開頭都會講的內容，故不再多費口舌說一遍了。

圖1. 經典K-means演算法

      值得一提的是關於聚類中心數目（K值）的選取，的確存在一種可行的方法，叫做Elbow Method：通過繪製K-means代價函式與聚類數目K的關係圖，選取直線拐點處的K值作為最佳的聚類中心數目。但在這邊不做過多的介紹，因為上述方法中的拐點在實際情況中是很少出現的。比較提倡的做法還是從實際問題出發，人工指定比較合理的K值，通過多次隨機初始化聚類中心選取比較滿意的結果。

三、K-means++演算法

    圖2. K-means++演算法

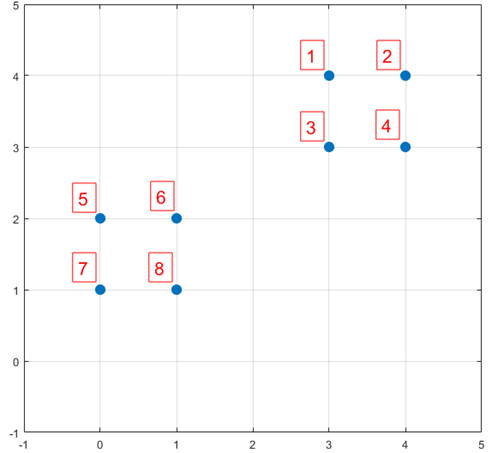
      下面結合一個簡單的例子說明K-means++是如何選取初始聚類中心的。資料集中共有8個樣本，分佈以及對應序號如下圖所示：

圖3. K-means++示例

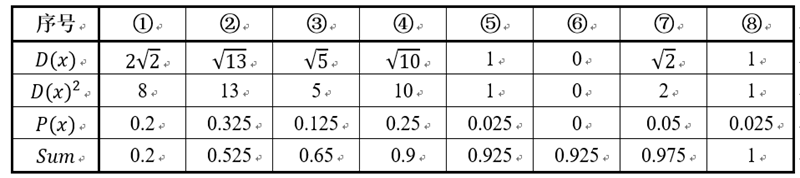
      假設經過圖2的步驟一後6號點被選擇為第一個初始聚類中心，那在進行步驟二時每個樣本的D(x)和被選擇為第二個聚類中心的概率如下表所示：

    其中的P(x)就是每個樣本被選為下一個聚類中心的概率。最後一行的Sum是概率P(x)的累加和，用於輪盤法選擇出第二個聚類中心。方法是隨機產生出一個0~1之間的隨機數，判斷它屬於哪個區間，那麼該區間對應的序號就是被選擇出來的第二個聚類中心了。例如1號點的區間為[0,0.2)，2號點的區間為[0.2, 0.525)。

      從上表可以直觀的看到第二個初始聚類中心是1號，2號，3號，4號中的一個的概率為0.9。而這4個點正好是離第一個初始聚類中心6號點較遠的四個點。這也驗證了K-means的改進思想：即離當前已有聚類中心較遠的點有更大的概率被選為下一個聚類中心。可以看到，該例的K值取2是比較合適的。當K值大於2時，每個樣本會有多個距離，需要取最小的那個距離作為D(x)。

四、ISODATA演算法

     放在最後也是最複雜的就是ISODATA演算法。正如之前所述，K-means和K-means++的聚類中心數K是固定不變的。而ISODATA演算法在執行過程中能夠根據各個類別的實際情況進行兩種操作來調整聚類中心數K：(1)分裂操作，對應著增加聚類中心數；(2)合併操作，對應著減少聚類中心數。

    下面首先給出ISODATA演算法的輸入（輸入的資料和迭代次數不再單獨介紹）：

      [1] 預期的聚類中心數目Ko：雖然在ISODATA執行過程中聚類中心數目是可變的，但還是需要由使用者指定一個參考標準。事實上，該演算法的聚類中心數目變動範圍也由Ko決定。具體地，最終輸出的聚類中心數目範圍是 [Ko/2, 2Ko]。

      [2] 每個類所要求的最少樣本數目Nmin：用於判斷當某個類別所包含樣本分散程度較大時是否可以進行分裂操作。如果分裂後會導致某個子類別所包含樣本數目小於Nmin，就不會對該類別進行分裂操作。

      [3] 最大方差Sigma：用於衡量某個類別中樣本的分散程度。當樣本的分散程度超過這個值時，則有可能進行分裂操作（注意同時需要滿足[2]中所述的條件）。

      [4] 兩個類別對應聚類中心之間所允許最小距離dmin：如果兩個類別靠得非常近（即這兩個類別對應聚類中心之間的距離非常小），則需要對這兩個類別進行合併操作。是否進行合併的閾值就是由dmin決定。

      相信很多人看完上述輸入的介紹後對ISODATA演算法的流程已經有所猜測了。的確，ISODATA演算法的原理非常直觀，不過由於它和其他兩個方法相比需要額外指定較多的引數，並且某些引數同樣很難準確指定出一個較合理的值，因此ISODATA演算法在實際過程中並沒有K-means++受歡迎。

      首先給出ISODATA演算法主體部分的描述，如下圖所示：

圖4. ISODATA演算法的主體部分

     上面描述中沒有說明清楚的是第5步中的分裂操作和第6步中的合併操作。下面首先介紹合併操作：

圖5. ISODATA演算法的合併操作

     最後是ISODATA演算法中的分裂操作。

圖6. ISODATA演算法的分裂操作

      最後，針對ISODATA演算法總結一下：該演算法能夠在聚類過程中根據各個類所包含樣本的實際情況動態調整聚類中心的數目。如果某個類中樣本分散程度較大（通過方差進行衡量）並且樣本數量較大，則對其進行分裂操作；如果某兩個類別靠得比較近（通過聚類中心的距離衡量），則對它們進行合併操作。

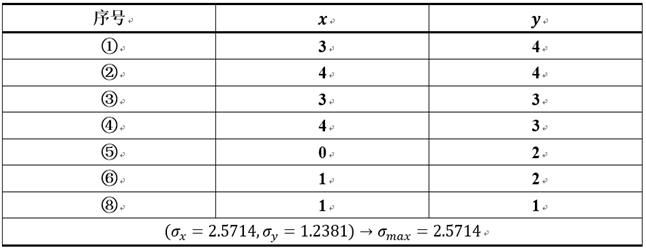
可能沒有表述清楚的地方是ISODATA-分裂操作的第1步和第2步。同樣地以圖三所示資料集為例，假設最初1，2，3，4，5，6，8號被分到了同一個類中，執行第1步和第2步結果如下所示：

      而在正確分類情況下（即1，2，3，4為一類；5，6，7，8為一類），方差為0.33。因此，目前的方差遠大於理想的方差，ISODATA演算法就很有可能對其進行分裂操作。

五、聚類演算法原始碼

      我已經將上述三種演算法整合成一個Matlab函式Clustering.m。讀者可以直接使用該函式對資料集進行聚類。由於程式碼比較長，而且程式碼外掛還不怎麼會用，就不在文中介紹了。需要使用的讀者可以點選下面的連結下載使用（歡迎Star和Fork，之後會不定期補充新的演算法和優化的）：

     使用方式非常簡單，目前支援三種形式的輸入，分別對應著上面的三種演算法：

     [centroid, result] = Clustering(data, ‘kmeans’, k , iteration);

     [centroid, result] = Clustering(data, ‘kmeans++’, k , iteration);

     [centroid, result] =

   Clustering(data, ‘isodata’, desired_k , iteration, minimum_n, maximum_variance, minimum_d);

      其中的輸入data是一個矩陣，每一行代表資料集中的一個樣本。其他輸入的意義與上面的演算法描述中一一對應。輸出的centroid是聚類中心的位置，result是每個樣本所對應的類別索引。

六、資料集測試

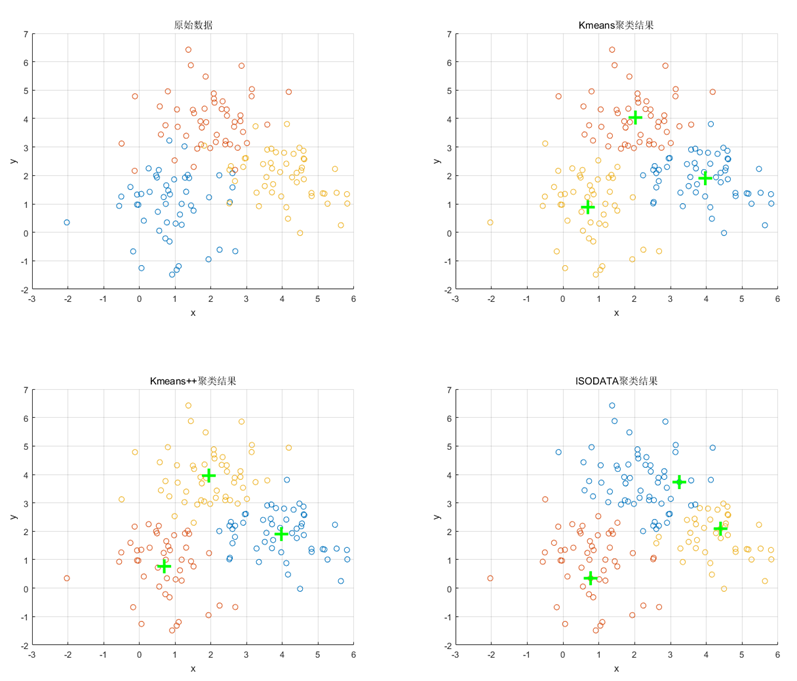
      最後以一個簡單的滿足二維高斯分佈的資料集為例，展示上述三種演算法的聚類結果，如下圖所示。

圖7. 一個簡單資料集上三種演算法的聚類效果（綠色加號代表聚類中心位置）