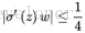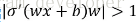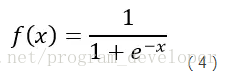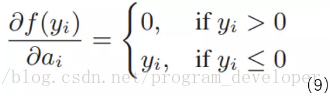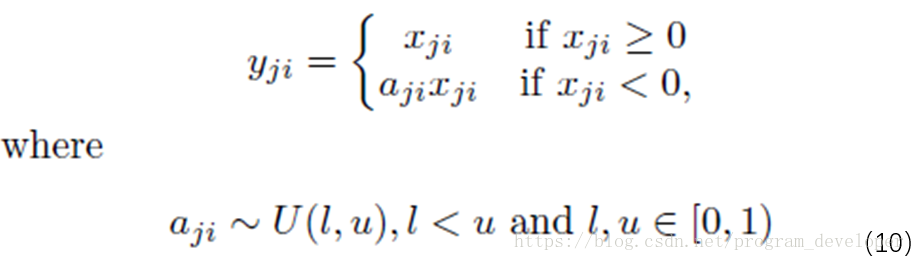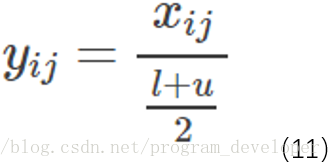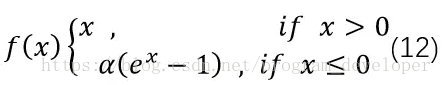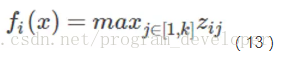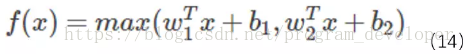啟用函式及其作用以及梯度消失、爆炸、神經元節點死亡的解釋
一、神經網路梯度消失與梯度爆炸
(1)簡介梯度消失與梯度爆炸
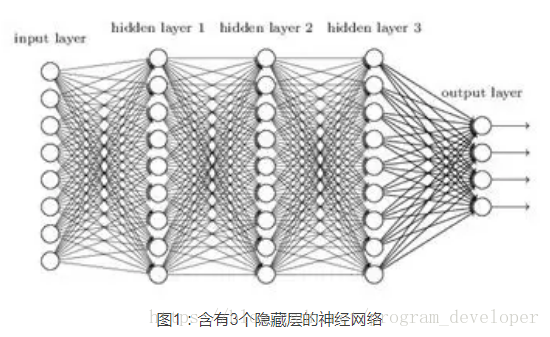
層數比較多的神經網路模型在訓練的時候會出現梯度消失(gradient vanishing problem)和梯度爆炸(gradient exploding problem)問題。梯度消失問題和梯度爆炸問題一般會隨著網路層數的增加變得越來越明顯。
例如，對於圖1所示的含有3個隱藏層的神經網路，梯度消失問題發生時，靠近輸出層的hidden layer 3的權值更新相對正常，但是靠近輸入層的hidden layer1的權值更新會變得很慢，導致靠近輸入層的隱藏層權值幾乎不變，扔接近於初始化的權值。這就導致hidden layer 1 相當於只是一個對映層，對所有的輸入做了一個函式對映，這時此深度神經網路的學習就等價於只有後幾層的隱藏層網路在學習。梯度爆炸的情況是：當初始的權值過大，靠近輸入層的hidden layer 1的權值變化比靠近輸出層的hidden layer 3的權值變化更快，就會引起梯度爆炸的問題。
(2)梯度不穩定問題
在深度神經網路中的梯度是不穩定的，在靠近輸入層的隱藏層中或會消失，或會爆炸。這種不穩定性才是深度神經網路中基於梯度學習的根本問題。
梯度不穩定的原因：前面層上的梯度是來自後面層上梯度的乘積。當存在過多的層時，就會出現梯度不穩定場景，比如梯度消失和梯度爆炸。
(3)產生梯度消失的根本原因
我們以圖2的反向傳播為例，假設每一層只有一個神經元且對於每一層都可以用公式1表示，其中σ為sigmoid函式，C表示的是代價函式，前一層的輸出和後一層的輸入關係如公式1所示。我們可以推匯出公式2。
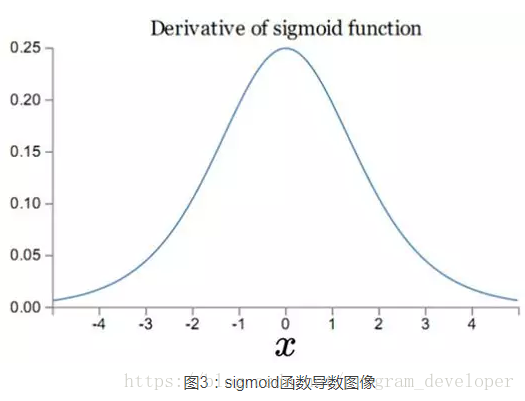
而sigmoid函式的導數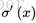
可見，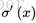
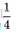
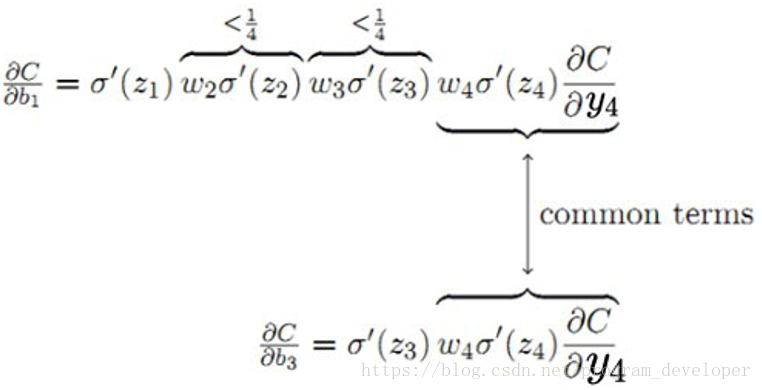
圖4：梯度變化的鏈式求導分析
對於圖4，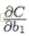
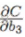
(4)產生梯度爆炸的根本原因
當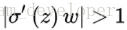
(5)當啟用函式為sigmoid時，梯度消失和梯度爆炸哪個更容易發生？
結論：梯度爆炸問題在使用sigmoid啟用函式時，出現的情況較少，不容易發生。
量化分析梯度爆炸時x的取值範圍：因導數最大為0.25，故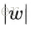
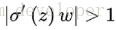
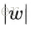=6.9時出現。因此僅僅在此很窄的範圍內會出現梯度爆炸的問題。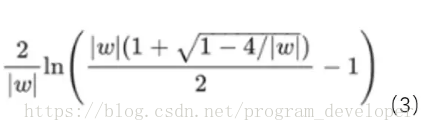 
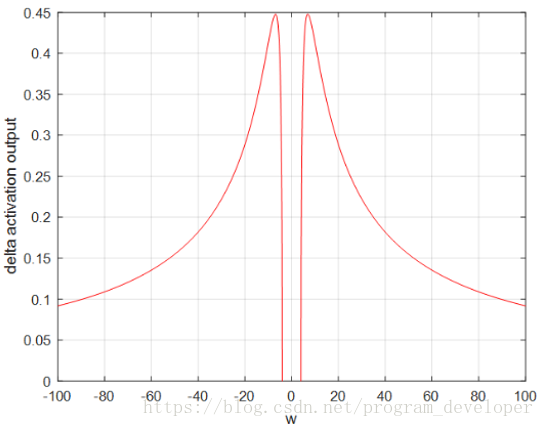
圖5：x的數值變化範圍
(6)如何解決梯度消失和梯度爆炸
梯度消失和梯度爆炸問題都是因為網路太深，網路權值更新不穩定造成的，本質上是因為梯度反向傳播中的連乘效應。對於更普遍的梯度消失問題，可以考慮一下三種方案解決：
用ReLU、Leaky-ReLU、P-ReLU、R-ReLU、Maxout等替代sigmoid函式。
用Batch Normalization。
LSTM的結構設計也可以改善RNN中的梯度消失問題。
二、幾種啟用函式的比較
由於使用sigmoid啟用函式會造成神經網路的梯度消失和梯度爆炸問題，所以許多人提出了一些改進的啟用函式，如：用ReLU、Leaky-ReLU、P-ReLU、R-ReLU、Maxout等替代sigmoid函式。下面我們具體來分析一下這幾個啟用函式的區別。
(1) Sigmoid
Sigmoid是常用的非線性的啟用函式，它的數學形式如公式4：
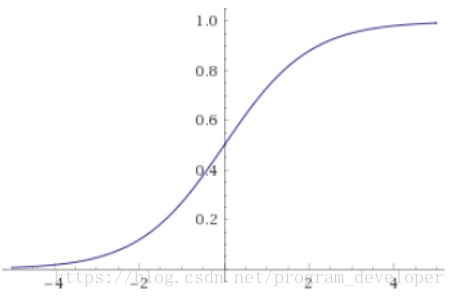
圖6：sigmoid函式影象
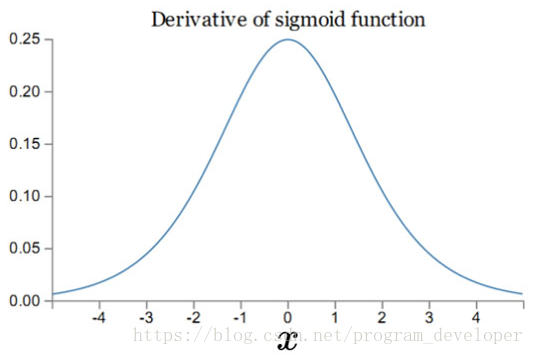
圖7：sigmoid導函式影象
Sigmoid函式在歷史上曾經非常的常用，輸出值範圍為[0,1]之間的實數。然而現在它已經不太受歡迎，實際中很少使用。原因是sigmoid存在3個問題：
1.sigmoid函式飽和使梯度消失(Sigmoidsaturate and kill gradients)。
我們從圖7可以看到sigmoid的導數都是小於0.25的，那麼在進行反向傳播的時候，梯度相乘結果會慢慢的趨近於0。這樣，幾乎就沒有梯度訊號通過神經元傳遞到前面層的梯度更新中，因此這時前面層的權值幾乎沒有更新，這就叫梯度消失。除此之外，為了防止飽和，必須對於權重矩陣的初始化特別留意。如果初始化權重過大，可能很多神經元得到一個比較小的梯度，致使神經元不能很好的更新權重提前飽和，神經網路就幾乎不學習。
2.sigmoid函式輸出不是“零為中心”(zero-centered)。
一個多層的sigmoid神經網路，如果你的輸入x都是正數，那麼在反向傳播中w的梯度傳播到網路的某一處時，權值的變化是要麼全正要麼全負。
圖8：sigmoid輸出不是關於原點對稱的影響
解釋下：當梯度從上層傳播下來，w的梯度都是用x乘以f的梯度，因此如果神經元輸出的梯度是正的，那麼所有w的梯度就會是正的，反之亦然。在這個例子中，我們會得到兩種權值，權值範圍分別位於圖8中一三象限。當輸入一個值時，w的梯度要麼都是正的要麼都是負的，當我們想要輸入一三象限區域以外的點時，我們將會得到這種並不理想的曲折路線（zig zag path），圖中紅色曲折路線。假設最優化的一個w矩陣是在圖8中的第四象限，那麼要將w優化到最優狀態，就必須走“之字形”路線，因為你的w要麼只能往下走(負數)，要麼只能往右走(正的)。優化的時候效率十分低下，模型擬合的過程就會十分緩慢。
如果訓練的資料並不是“零為中心”，我們將多個或正或負的梯度結合起來就會使這種情況有所緩解，但是收斂速度會非常緩慢。該問題相對於神經元飽和問題來說還是要好很多。具體可以這樣解決，我們可以按batch去訓練資料，那麼每個batch可能得到不同的訊號或正或負，這個批量的梯度加起來後可以緩解這個問題。
3.指數函式的計算是比較消耗計算資源的。
(2) tanh
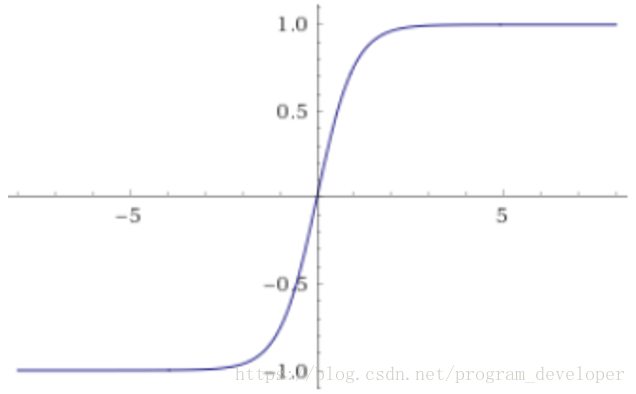
圖9：tanh(x)的函式影象
tanh函式跟sigmoid還是很像的，實際上，tanh是sigmoid的變形如公式5所示。tanh的具體公式如公式6所示。
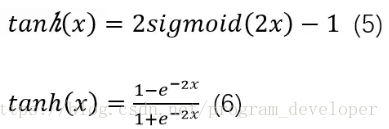
tanh與sigmoid不同的是，tanh是“零為中心”的。因此，實際應用中，tanh會比sigmoid更好一些。但是在飽和神經元的情況下，還是沒有解決梯度消失問題。
優點：
1.tanh解決了sigmoid的輸出非“零為中心”的問題。
缺點：
1.依然有sigmoid函式過飽和的問題。
2.依然指數運算。
(3) ReLU
近年來，ReLU函式變得越來越受歡迎。全稱是Rectified Linear Unit，中文名字：修正線性單元。ReLU是Krizhevsky、Hinton等人在2012年《ImageNet Classification with Deep Convolutional Neural Networks》論文中提出的一種線性且不飽和的啟用函式。它的數學表示式如7所示：
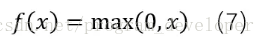
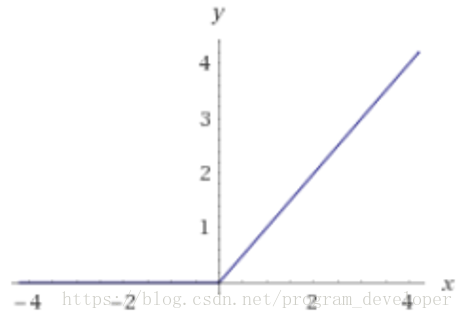
圖10：ReLU函式影象
優點：
1.ReLU解決了梯度消失的問題，至少x在正區間內，神經元不會飽和。
2.由於ReLU線性、非飽和的形式，在SGD中能夠快速收斂。
3.計算速度要快很多。ReLU函式只有線性關係，不需要指數計算，不管在前向傳播還是反向傳播，計算速度都比sigmoid和tanh快。
缺點：
1.ReLU的輸出不是“零為中心”(Notzero-centered output)。
2.隨著訓練的進行，可能會出現神經元死亡，權重無法更新的情況。這種神經元的死亡是不可逆轉的死亡。
解釋：訓練神經網路的時候，一旦學習率沒有設定好，第一次更新權重的時候，輸入是負值，那麼這個含有ReLU的神經節點就會死亡，再也不會被啟用。因為：ReLU的導數在x>0的時候是1，在x<=0的時候是0。如果x<=0，那麼ReLU的輸出是0，那麼反向傳播中梯度也是0，權重就不會被更新，導致神經元不再學習。
也就是說，這個ReLU啟用函式在訓練中將不可逆轉的死亡，導致了訓練資料多樣化的丟失。在實際訓練中，如果學習率設定的太高，可能會發現網路中40%的神經元都會死掉，且在整個訓練集中這些神經元都不會被啟用。所以，設定一個合適的較小的學習率，會降低這種情況的發生。為了解決神經元節點死亡的情況，有人提出了Leaky ReLU、P-ReLu、R-ReLU、ELU等啟用函式。
(4) Leaky ReLU
ReLU是將所有的負值設定為0，造成神經元節點死亡情況。相反，Leaky ReLU是給所有負值賦予一個非零的斜率。Leaky ReLU啟用函式是在聲學模型(2013)中首次提出來的。它的數學表示式如公式8所示。
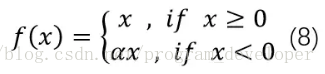
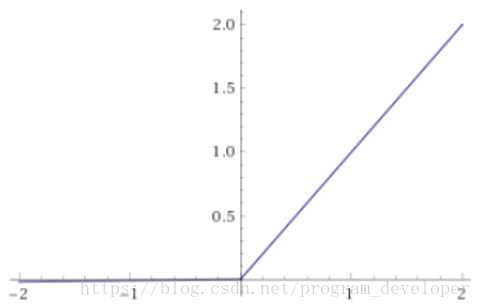
圖11：Leaky ReLU函式影象
Leaky ReLU很好的解決了“dead ReLU”的問題。因為Leaky ReLU保留了x小於0時的梯度，在x小於0時，不會出現神經元死亡的問題。對於Leaky ReLU給出了一個很小的負數梯度值α，這個值是很小的常數。比如：0.01。這樣即修正了資料分佈，又保留了一些負軸的值，使得負軸資訊不會全部丟失。但是這個α通常是通過先驗知識人工賦值的。
優點：
1.神經元不會出現死亡的情況。
2.對於所有的輸入，不管是大於等於0還是小於0，神經元不會飽和。
2.由於Leaky ReLU線性、非飽和的形式，在SGD中能夠快速收斂。
3.計算速度要快很多。Leaky ReLU函式只有線性關係，不需要指數計算，不管在前向傳播還是反向傳播，計算速度都比sigmoid和tanh快。
缺點：
1.Leaky ReLU函式中的α，需要通過先驗知識人工賦值。
擴充套件材料：
1.Andrew L. Maas, Awni Y. Hannum and Andrew Y. Ng. Rectified NonlinearitiesImprove Neural Network Acoustic Models (PDF). ICML.2013. 該論文提出了Leaky ReLU函式。
2.He K, Zhang X, Ren S, et al. Delving deepinto rectifiers: Surpassing human-level performance on imagenetclassification[C]//Proceedings of the IEEE international conference on computervision. 2015: 1026-1034. 該論文介紹了用Leaky ReLU函式的好處。
(5) PReLU
PReLU的英文全稱為“Parametric ReLU”，我翻譯為“帶引數的線性修正單元”。我們觀察Leaky ReLU可知，在神經網路中通過損失函式對α求導數，我們是可以求得的。那麼，我們可不可以將它作為一個引數進行訓練呢？在Kaiming He的論文《Delving deepinto rectifiers: Surpassing human-level performance on imagenet classification》中指出，α不僅可以訓練，而且效果更好。
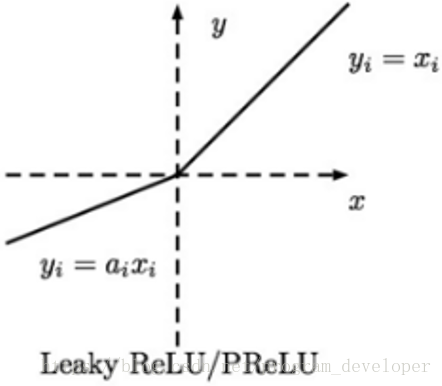
圖12：PReLU函式影象
公式9非常簡單，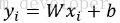
擴充套件材料：
He K, Zhang X, Ren S, et al. Delving deepinto rectifiers: Surpassing human-level performance on imagenetclassification[C]//Proceedings of the IEEE international conference on computervision. 2015: 1026-1034. 該論文作者對比了PReLU和ReLU在ImageNet model A的訓練效果。
(6) RReLU
RReLU的英文全稱是“Randomized Leaky ReLU”，中文名字叫“隨機修正線性單元”。RReLU是Leaky ReLU的隨機版本。它首次是在Kaggle的NDSB比賽中被提出來的。
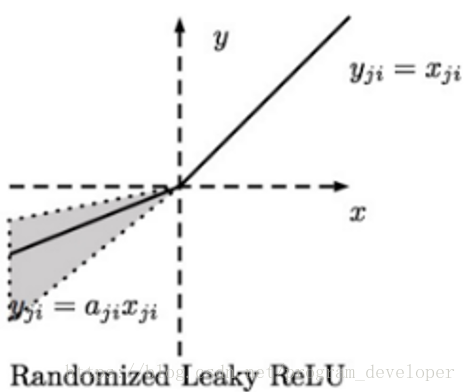
圖13：Randomized Leaky ReLU函式影象
RReLU的核心思想是，在訓練過程中，α是從一個高斯分佈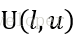
在測試階段，把訓練過程中所有的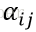
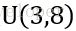
特點：
1.RReLU是Leaky ReLU的random版本，在訓練過程中，α是從一個高斯分佈中隨機出來的，然後再測試過程中進行修正。
2.數學形式與PReLU類似，但RReLU是一種非確定性啟用函式，其引數是隨機的。
(7)ReLU、Leaky ReLU、PReLU和RReLU的比較
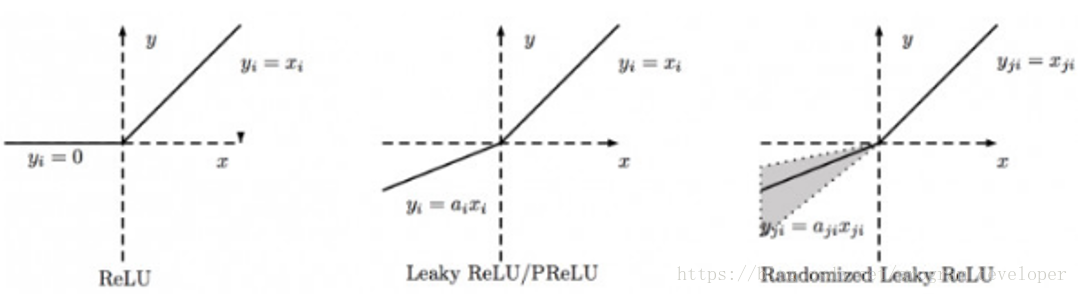
圖14：ReLU、Leaky ReLU、PReLU、RReLU函式影象
PReLU中的α是根據資料變化的；
Leaky ReLU中的α是固定的；
RReLU中的α是一個在給定範圍內隨機抽取的值，這個值在測試環節就會固定下來。
擴充套件材料：
Xu B, Wang N, Chen T, et al. Empiricalevaluation of rectified activations in convolutional network[J]. arXiv preprintarXiv:1505.00853, 2015. 在這篇論文中作者對比了ReLU、LReLU、PReLU、RReLU在CIFAR-10、CIFAR-100、NDSB資料集中的效果。
（8）ELU
ELU的英文全稱是“Exponential Linear Units”，中文全稱是“指數線性單元”。它試圖將啟用函式的輸出平均值接近零，從而加快學習速度。同時，它還能通過正值的標識來避免梯度消失的問題。根據一些研究顯示，ELU分類精確度是高於ReLU的。公式如12式所示。
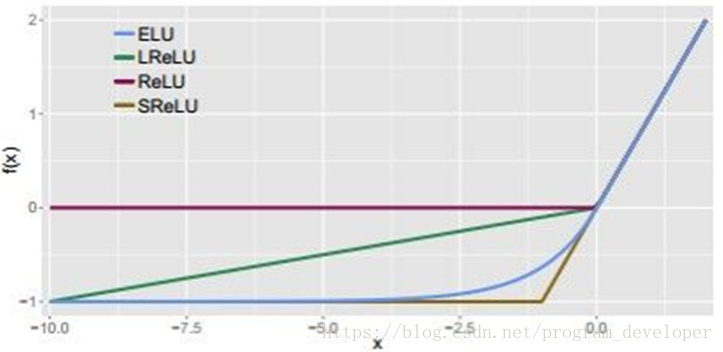
圖15：ELU與其他幾種啟用函式的比較圖
優點：
ELU包含了ReLU的所有優點。
神經元不會出現死亡的情況。
ELU啟用函式的輸出均值是接近於零的。
缺點：
計算的時候是需要計算指數的，計算效率低的問題。
擴充套件材料：
Clevert D A, Unterthiner T, Hochreiter S. Fastand accurate deep network learning by exponential linear units (elus)[J]. arXivpreprint arXiv:1511.07289, 2015. 這篇論文提出了ELU函式。
（9）Maxout
Maxout “Neuron” 是由Goodfellow等人在2013年提出的一種很有特點的神經元，它的啟用函式、計算的變數、計算方式和普通的神經元完全不同，並有兩組權重。先得到兩個超平面，再進行最大值計算。啟用函式是對ReLU和Leaky ReLU的一般化歸納，沒有ReLU函式的缺點，不會出現啟用函式飽和神經元死亡的情況。Maxout出現在ICML2013上，作者Goodfellow將maxout和dropout結合，稱在MNIST，CIFAR-10，CIFAR-100，SVHN這4個數據集上都取得了start-of-art的識別率。Maxout公式如13所示。
其中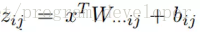
分析公式14可以注意到，ReLU和Leaky ReLU都是它的一個變形。比如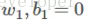
優點：
Maxout具有ReLU的所有優點，線性、不飽和性。
同時沒有ReLU的一些缺點。如：神經元的死亡。
缺點：
從這個啟用函式的公式14中可以看出，每個neuron將有兩組w，那麼引數就增加了一倍。這就導致了整體引數的數量激增。
擴充套件材料：
Goodfellow I J, Warde-Farley D, Mirza M, et al.Maxout networks[J]. arXiv preprint arXiv:1302.4389, 2013. Goodfellow的這篇論文提出了Maxout，感興趣可以瞭解一下。
總結：怎麼選擇啟用函式？
關於啟用函式的選取，目前還不存在定論，在實踐過程中更多還是需要結合實際情況，考慮不同啟用函式的優缺點綜合使用。我在這裡給大家一點在訓練模型時候的建議。
1.通常來說，不會把各種啟用函式串起來在一個網路中使用。
2.如果使用ReLU，那麼一定要小心設定學習率(learning rate),並且要注意不要讓網路中出現很多死亡神經元。如果死亡神經元過多的問題不好解決，可以試試Leaky ReLU、PReLU、或者Maxout。
3.儘量不要使用sigmoid啟用函式，可以試試tanh，不過個人感覺tanh的效果會比不上ReLU和Maxout。
Reference:
1.Andrew L. Maas, Awni Y. Hannum and Andrew Y. Ng. Rectified NonlinearitiesImprove Neural Network Acoustic Models (PDF). ICML.2013. 該論文提出了Leaky ReLU函式。
2.He K, Zhang X, Ren S, et al. Delving deepinto rectifiers: Surpassing human-level performance on imagenetclassification[C]//Proceedings of the IEEE international conference on computervision. 2015: 1026-1034. 該論文介紹了用Leaky ReLU函式的好處。
3.He K, Zhang X, Ren S, et al. Delving deepinto rectifiers: Surpassing human-level performance on imagenetclassification[C]//Proceedings of the IEEE international conference on computervision. 2015: 1026-1034. 該論文作者對比了PReLU和ReLU在ImageNet model A的訓練效果。
4.Xu B, Wang N, Chen T, et al. Empiricalevaluation of rectified activations in convolutional network[J]. arXiv preprintarXiv:1505.00853, 2015. 在這篇論文中作者對比了ReLU、LReLU、PReLU、RReLU在CIFAR-10、CIFAR-100、NDSB資料集中的效果。
5.Clevert D A, Unterthiner T, Hochreiter S. Fastand accurate deep network learning by exponential linear units (elus)[J]. arXivpreprint arXiv:1511.07289, 2015. 這篇論文提出了ELU函式。
6.Goodfellow I J, Warde-Farley D, Mirza M, et al.Maxout networks[J]. arXiv preprint arXiv:1302.4389, 2013. Goodfellow的這篇論文提出了Maxout，感興趣可以瞭解一下。