約瑟夫問題是個有名的問題：N個人圍成一圈，從第一個開始報數，第M個將被殺掉，最後剩下一個，其餘人都將被殺掉。例如N=6，M=5，被殺掉的順序是：5，4，6，2，3，1。
給定N個人和m,計算最後獲救者的編號，求解的思路是一種遞推思想。
我們知道第一個人（編號一定是（m-1） mod n) 出列之後，剩下的n-1個人組成了一個新的約瑟夫環（以編號為k=m mod n的人開始）：
k k+1 k+2 … n-2,n-1,0,1,2,… k-2，並且從k開始報0。
我們把他們的編號做一下轉換：
k –> 0
k+1 –> 1
k+2 –> 2
…
…
k-2 –> n-2
變換後就完完全全成為了（n-1）個人報數的子問題，假如我們知道這個子問題的解：例如x是最終的勝利者，那麼根據上面這個表把這個x變回去不剛好就是n個人情況的解嗎？！！變回去的公式很簡單，相信大家都可以推出來：x’=(x+k) mod n
如何知道（n-1）個人報數的問題的解？對，只要知道（n-2）個人的解就行了。（n-2）個人的解呢？當然是先求（n-3）的情況 —- 這顯然就是一個倒推問題！好了，思路出來了，下面寫遞推公式：
令f表示i個人玩遊戲報m退出最後勝利者的編號，最後的結果自然是f[n]
遞推公式

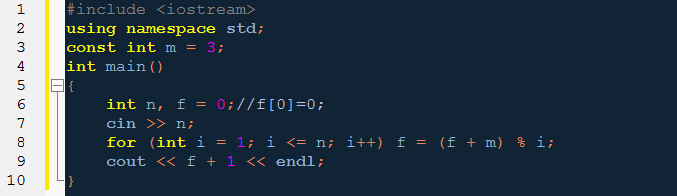
約瑟夫環變形 先引入Joseph遞推公式，設有n個人（0,…,n-1），數m，則第i輪出局的人為
f(i)=(f(i-1)+m-1)%(n-i+1)；
f(0)=0;
f(i) 表示當前子序列中要退出的那個人（當前序列編號為0~(n-i));

拿個例子說：K=4,M=30;

f(0)=0;

f(1)=(f(0)+30-1)%8=5; 序列（0,1,2,3,4,5,6,7）中的5

f(2)=(f(1)+30-1)%7=6; 序列（0,1,2,3,4,6,7）中的7

f(3)=(f(2)+30-1)%6=5; 序列（0,1,2,3,4,6）中的6

f(4)=(f(3)+30-1)%5=4; 序列（0,1,2,3,4）中的4

……..

依據題意，前K個退出的人必定是後K個人，所以只要前k輪中只要有一次f(i)小於k則此m不符合題意。

參考文章：

• ζёСяêτ - 小優YoU

根據這樣的思路，求解poj 1012就很容易了。

先打表預處理，把每一個k的結果儲存在Joseph[k]中，輸出，避免超時。

參考程式碼+部分註釋：

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <map>
#include <vector>
#include <queue>
#include <cstring>
#include <cmath>
#include <climits>
#define eps 1e-8
using namespace std;
typedef long long ll;
const int INF=INT_MAX;
const int maxn = 110;
int k,ans[20],Joseph[20];
void init()
{
    for(int k=1;k<=14;k++){
        int m=1,n=2*k;
        while(1){
          bool ok=true;
          ans[0]=0;
          for(int i=1;i<=k;i++){
            ans[i]=(ans[i-1]+m-1)%(n+1-i);//遞推
            if(ans[i]<k) {ok=false;break;}//不滿足條件就標記
          }
          if(ok) break;
          m++;
        }
        Joseph[k]=m;
    }
}
int main()
{
  // freopen("input.txt","r",stdin);
   init();
   while(cin>>k&&k){
     cout<<Joseph[k]<<endl;
   }
   return 0;
}