李航·統計學習方法筆記·第6章 logistic regression與最大熵模型(1)·邏輯斯蒂迴歸模型
第6章 logistic regression與最大熵模型(1)·邏輯斯蒂迴歸模型
標籤(空格分隔): 機器學習教程·李航統計學習方法
邏輯斯蒂:logistic
李航書中稱之為:邏輯斯蒂迴歸模型
周志華書中稱之為:對數機率迴歸模型
Andrew NG書中稱之為:邏輯迴歸
……好吧!好多不同的名稱,其實都是一種方法,暈了好久……
為了利用邏輯斯蒂分佈去進行迴歸問題的分析,首先,必須知道什麼是邏輯斯蒂分佈,所以,本節主要討論邏輯斯蒂分佈,它是一個連續分佈,與高斯分佈非常像;
1 Logistic distribution
The Logistic distribution is a continuous probability density function that is symmetric
and uni-modal. It is similar in appearance to the Normal distribution and in practical
applications, the two distributions cannot be distinguished from one another.
1.1 一維邏輯斯蒂分佈的數學定義
- 分佈函式
F(x)=11+e−(x−μ)/σ
注1:也可以寫成
F(x)=e(x−μ)/σe(x−μ)/σ+1
注2:分佈函式(即概率累積函式)的導數
F′(x)=−(1+e−(x−μ)/σ)′(1+e−(x−μ)/σ)2=−(−1σ)e−(x−μ)/σ(1+e−(x−μ)/σ)2=1σe−(x−μ)/σ(1+e−(x−μ)/σ)2 - 概率密度函式
f(x)=1σ∗e−(x−μ)/σ(1+e−(x−μ)/σ)2
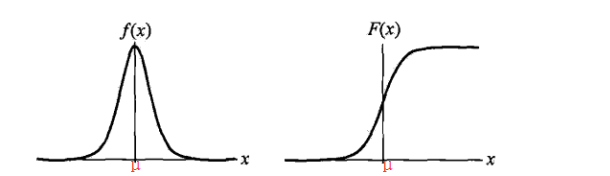
- logistic涉及兩個引數
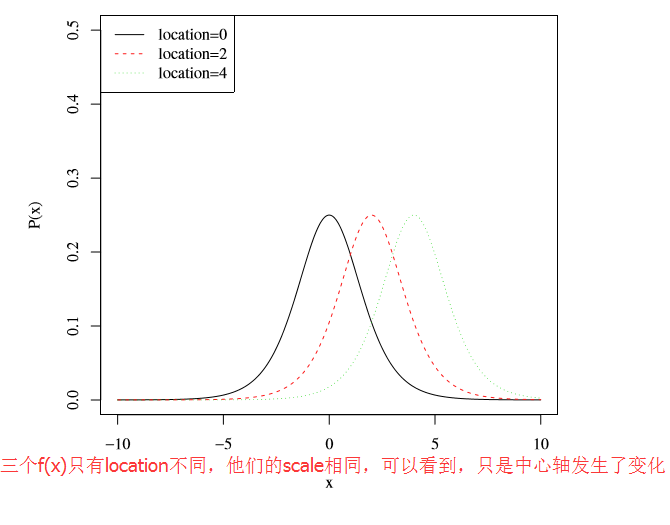
μ :location,控制分佈函式的中心位置,或者說是概率密度函式對稱軸的位置
σ :scale,該引數控制著f 的寬和高;其值越大,(x)f(x) 越矮越胖
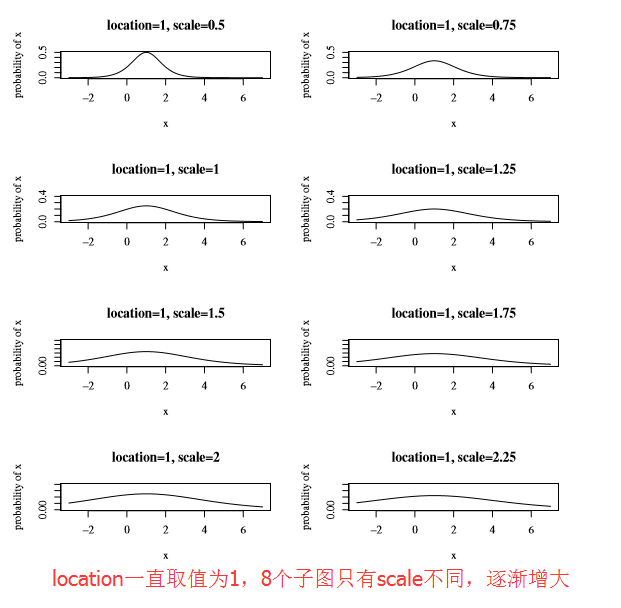
注:其實該引數σ 與正態分佈的σ 含義相同,只不過相差了一個係數π23 (這個數字來自於logistic distribution的方差),
1.2 logistic分佈的均值和方差
- 均值:
E(x)=μ - 方差:
Var(x)=13(πσ)2 - 考察高斯分佈
N(μ,σ2) ,它的均值為μ ,方差為σ2 :
- 可以看到,logistic分佈的方差
σ2π23 與高斯分佈方差只是差了一個常數項π23 - 所以說,logistic分佈與高斯分佈非常相似
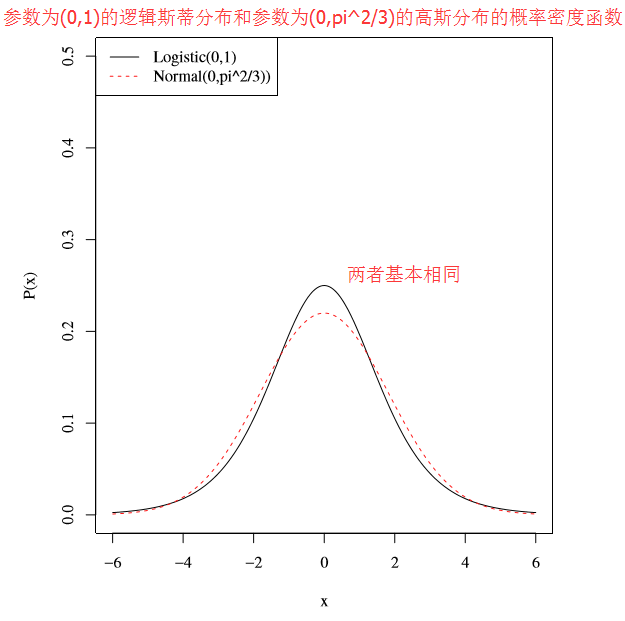
- 如下圖所示,分別繪製出了引數為(0,1)的logistic分佈和引數為(0,
π23 )的高斯分佈的密度函式,此時,二者的方差取值相同(都為π ),可以看到,此時的logistic概率密度函式和高斯函式概率密度函式非常接近23
- 可以看到,logistic分佈的方差
1.3 何時需要用到Logistic分佈
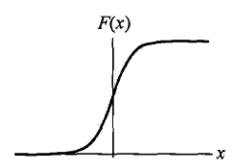
由於logistic分佈的分佈函式(S型)的良好的數學性質,使得它的概率密度函式具有對稱性,從而,經常使用logistic分佈區近似其他具有對稱概率密度函式的分佈
logistic分佈的這種S-shapesd的分佈,稱為Logistic regression model,其用來對某個輸入最可能的輸出進行預測
logistic CDF(分佈函式、cumulative distribution function)的S-shaped曲線,實際上可以描述了某一個事件發生的可能性
2. 二項邏輯斯蒂迴歸模型及其特點
2.1 二項邏輯斯蒂迴歸模型
- 上面討論了邏輯斯蒂分佈,接下來將該分佈應用到機器學習的分類問題中!
- 假設我們要解決的問題為一個二分類問題,那麼,可以利用邏輯斯蒂分佈來對二分類模型建模,即對於一個樣本x,它的類別要麼為1,要麼為0,我們設定它為1的概率為邏輯斯蒂分佈中的概率分佈形式,那麼,它為0的概率也就是1-P(y=0);
- 這裡的“二項”一詞,與二項分佈的意義相同(一次試驗的結果要麼為1要麼為0),一個樣本類別要麼為1要麼為0
二項邏輯斯蒂迴歸模型的應用場景:
兩類分類問題,期Y∈{1,0}
另:樣本x 具有n個特徵,即x∈Rn 二項邏輯斯蒂迴歸模型具體形式:
⎧⎩⎨⎪⎪⎪⎪⎪⎪P(Y=1|x)=exp(w⋅x+b)1+exp(w⋅x+b)P
