原文發於個人部落格

前言

說好的要做個有逼格的技術部落格，雖然這篇依然沒什麼水平，但總算走出了第一步，希望以後每天都能進步一點點吧！

接觸機器學習也一年多了，也學了很多演算法，而PCA是資料預處理中一個很重要的演算法，當時學習的時候也在網上看了很多資料，沒想到一個簡單的PCA也有著嚴密的數學推導，終於知道當年研究生考試為什麼數學要考這麼難了。

這篇文章主要是對PCA演算法的一個總結，數學原理部分主要來自PCA的數學原理，並對其進行了總結（其實人家已經總結的很棒了），然後通過Scikit-learn中的一個例子講解PCA的使用，最後用Python編寫一個簡單的PCA演算法。

正文

數學概念介紹

方差：用來衡量隨機變數與其數學期望（均值）之間的偏離程度。統計中的方差（樣本方差）是各個資料分別與其平均數之差的平方的和的平均數。

協方差：度量兩個隨機變數關係的統計量，協方差為0的兩個隨機變數是不相關的。

協方差矩陣：在統計學與概率論中，協方差矩陣的每個元素是各個向量元素之間的協方差。特殊的，矩陣對角線上的元素分別是向量的方差。

—— 摘自百度百科

特別是協方差矩陣的概念非常重要。

PCA介紹

主成分分析（Principal Component Analysis），是一種用於探索高維資料的技術。PCA通常用於高維資料集的探索與視覺化。還可以用於資料壓縮，資料預處理等。PCA可以把可能具有線性相關性的高維變數合成為線性無關的低維變數，稱為主成分（principal components）

注意：降維就意味著資訊的丟失，這一點一定要明確，如果用原始資料在模型上沒有效果，期望通過降維來進行改善這是不現實的，不過鑑於實際資料本身常常存在的相關性，我們可以想辦法在降維的同時將資訊的損失儘量降低。當你在原資料上跑了一個比較好的結果，又嫌它太慢模型太複雜時候才可以採取PCA降維。

PCA數學理論

基

二維空間預設(1,0)和(0,1)為一組基。
其實任何兩個線性無關的二維向量都可以成為一組基。因為正交基有較好的性質，所以一般使用的基都是正交的。

例如：只有一個(3,2)本身是不能夠精確表示一個向量的。這裡的3實際表示的是向量在x軸上的投影值是3，在y軸上的投影值是2。也就是說我們其實隱式引入了一個定義：以x軸和y軸上正方向長度為1的向量為標準，預設選擇(1,0)和(0,1)為基。

內積

向量A和B的內積公式為：

我們希望基的模是1，因為從內積的意義可以看到，如果基的模是1，那麼就可以方便的用向量點乘基而直接獲得其在新基上的座標了，即 向量在基上的投影=向量與基的內積=座標。

基變換的矩陣表示

將一組向量的基變換表示為矩陣的相乘。一般的，如果我們有M個N維向量，想將其變換為由R個N維向量（R個基）表示的新空間中，那麼首先將R個基按行組成矩陣P，然後將待變換向量按列組成矩陣X，那麼兩矩陣的乘積就是變換結果。R可以小於N，而R決定了變換後資料的維數。也就是說，我們可以將一N維資料變換到更低維度的空間中去，變換後的維度取決於基的數量。
因此這種矩陣相乘可以表示降維變換：

兩個矩陣相乘的意義：將右邊矩陣中的每一列列向量變換到左邊矩陣中每一行行向量為基所表示的空間中。

優化目標

如何選擇基才是最優的。或者說，如果我們有一組N維向量，現在要將其降到R維，那麼我們應該如何選擇R個基才能最大程度保留原有的資訊？

對於一個二維空間：要在二維平面中選擇一個方向，將所有資料都投影到這個方向所在直線上，用投影值表示原始記錄。這是一個實際的二維降到一維的問題。那麼如何選擇這個方向才能儘量保留最多的原始資訊呢？一種直觀的看法是：希望投影后的投影值儘可能分散，而這種分散程度，可以用數學上的方差來表述。

對於上面二維降成一維的問題來說，找到那個使得方差最大的方向就可以了。不過對於更高維，還有一個問題需要解決。考慮三維降到二維問題，與之前相同，首先我們希望找到一個方向使得投影后方差最大，這樣就完成了第一個方向的選擇，繼而我們選擇第二個投影方向。如果我們還是單純只選擇方差最大的方向，很明顯，這個方向與第一個方向應該是“幾乎重合在一起”，顯然這樣的維度是沒有用的，因此，應該有其他約束條件。從直觀上說，讓兩個不同維度儘可能表示更多的原始資訊，我們是不希望它們之間存在（線性）相關性的，因為相關性意味著兩個維度不是完全線性獨立，必然存在重複表示的資訊。

數學上用協方差表示兩個維度的相關性，當協方差為0時，表示兩個維度完全獨立。為了讓協方差為0，我們選擇第二個基時只能在與第一個基正交的方向上選擇，因此最終選擇的兩個方向一定是正交的。

降維問題的優化目標：將一組N維向量降為R維，其目標是選擇R個單位正交基，使得原始資料變換到這組基上後，各維度兩兩間的協方差為0，而每個維度的方差則儘可能大（在正交的約束下，取最大的R個方差）。

協方差矩陣

上面推匯出優化目標，那麼具體該怎麼實現呢，下面就用到了協方差矩陣。回顧一下，協方差矩陣的每個元素是各個向量元素之間的協方差，特殊的，矩陣對角線上的元素分別是各個向量的方差。

設原始矩陣為X(N×M)，表示M個N維向量，其協方差矩陣為C(N×N)；P(R×N)為變換矩陣；Y(R×M)為目標矩陣, 其協方差矩陣為D。我們要求降維後的矩陣Y的每一維包含的資料足夠分散，也就是每一行（維）方差足夠大，而且要求行之間的元素線性無關，也就是要求行之間的協方差全部為0，這就要求協方差矩陣D的對角線元素足夠大，除對角線外元素都為0。
相當於對C進行協方差矩陣對角化。

具體推導如下：

C是X的協方差矩陣，是實對稱矩陣，整個PCA降維過程其實就是一個實對稱矩陣對角化的過程。

PCA具體演算法步驟

設有M個N維資料:

1. 將原始資料按列組成N行M列矩陣X

2. 將X的每一行進行零均值化，即減去每一行的均值

3. 求出X的協方差矩陣C

4. 求出協方差矩陣C的特徵值及對應的特徵向量，C的特徵值就是Y的每維元素的方差，也是D的對角線元素，從大到小沿對角線排列構成D。

5. 將特徵向量按對應特徵值大小從上到下按行排列成矩陣，根據實際業務場景，取前R行組成矩陣P

6. Y=PX即為降到R維後的目標矩陣

Scikit-learn PCA例項分析

Scikit-learn是Python下著名的機器學習庫，關於它我在這裡就不多做介紹了，反正很好很強大。

首先資料選用經典的手寫字元資料。

from sklearn import datasets
digits = datasets.load_digits()
x = digits.data                                              #輸入資料
y = digits.target                                            #輸出資料

PCA的呼叫也很簡單。

from sklearn import decomposition
pca = decomposition.PCA()
pca.fit(x)

視覺化，matplotlib是Python下的繪相簿，功能也是十分強大。

import matplotlib.pyplot as plt
plt.figure()
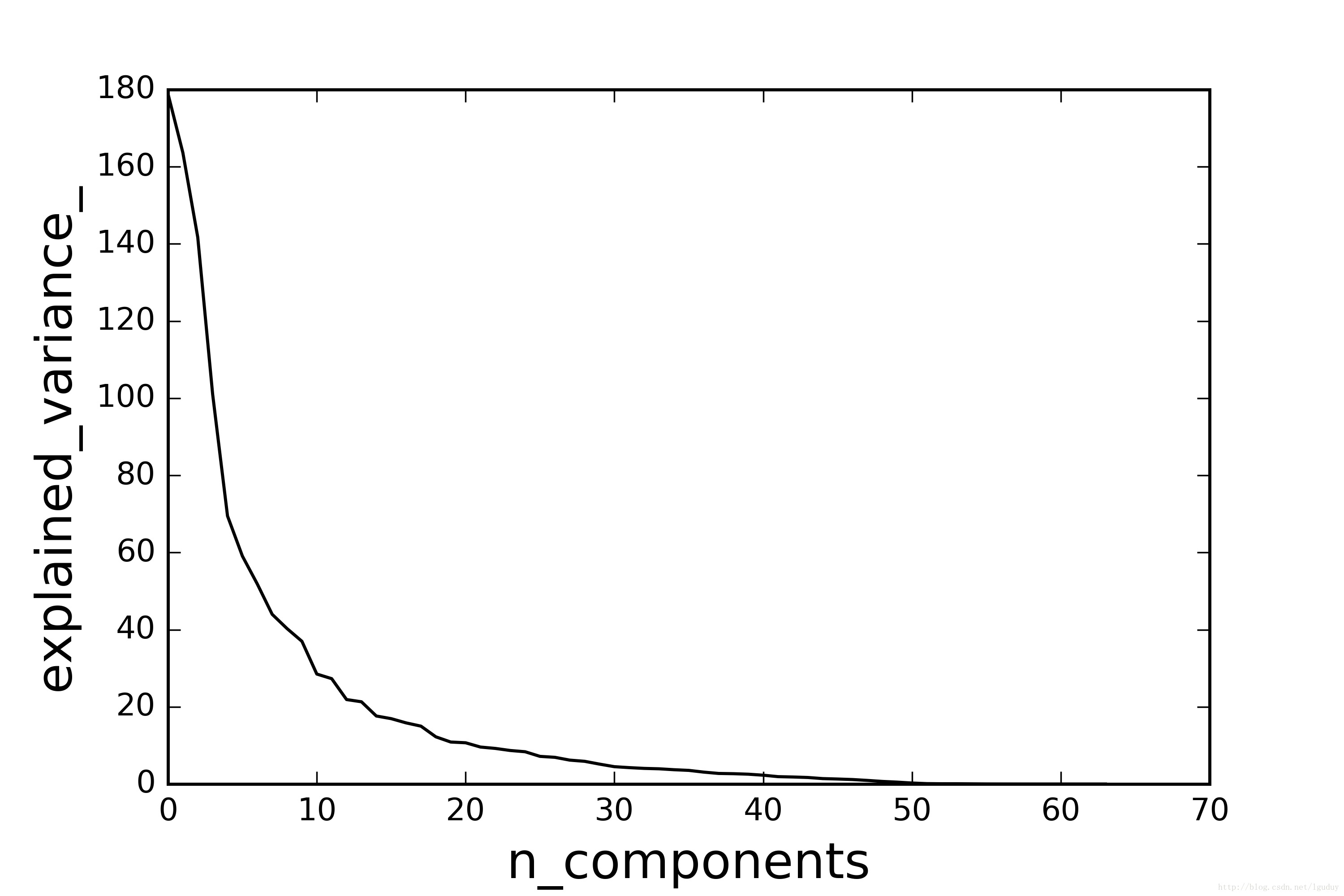
plt.plot(pca.explained_variance_, 'k', linewidth=2)
plt.xlabel('n_components', fontsize=16)
plt.ylabel('explained_variance_', fontsize=16)
plt.show()

pca.explained_variance_ 就是上面協方差矩陣D的對角線元素，如下圖所示：

至於到底降到多少維度，主要取決於方差，具體的方法可以採用交叉驗證。

實現PCA演算法

基於Nnmpy, Pandas, Matploylib實現PCA並可視化結果。整體程式碼很簡單，按照上面總結的演算法步驟一步一步地計算，Numpy和Pandas的功能很強大，你能想到的運算幾乎都有。

首先定義異常類：

class DimensionValueError(ValueError):
    """定義異常類"""
    pass

定義PCA類：

class PCA(object):
    """定義PCA類"""
    def __init__(self, x, n_components=None):
        self.x = x
        self.dimension = x.shape[1]

        if n_components and n_components >= self.dimension:
            raise DimensionValueError("n_components error")

        self.n_components = n_components

接下來就是計算協方差矩陣，特徵值，特徵向量，為了方便下面的計算，我把特徵值和特徵向量整合在一個dataframe內，並按特徵值的大小降序排列：

    def cov(self):
        """求x的協方差矩陣"""
        x_T = np.transpose(self.x)                           #矩陣轉置
        x_cov = np.cov(x_T)                                  #協方差矩陣
        return x_cov

    def get_feature(self):
        """求協方差矩陣C的特徵值和特徵向量"""
        x_cov = self.cov()
        a, b = np.linalg.eig(x_cov)
        m = a.shape[0]
        c = np.hstack((a.reshape((m,1)), b))
        c_df = pd.DataFrame(c)
        c_df_sort = c_df.sort(columns=0, ascending=False)    
        return c_df_sort

最後就是降維，用了兩種方式，指定維度降維和根據方差貢獻率自動降維，預設方差貢獻率為99%：

    def reduce_dimension(self):
        """指定維度降維和根據方差貢獻率自動降維"""
        c_df_sort = self.get_feature()
        varience = self.explained_varience_()

        if self.n_components:                                #指定降維維度
            p = c_df_sort.values[0:self.n_components, 1:]
            y = np.dot(p, np.transpose(self.x))              
            return np.transpose(y)

        varience_sum = sum(varience)                         
        varience_radio = varience / varience_sum

        varience_contribution = 0
        for R in xrange(self.dimension):
            varience_contribution += varience_radio[R]       
            if varience_contribution >= 0.99:
                break

        p = c_df_sort.values[0:R+1, 1:]                      #取前R個特徵向量
        y = np.dot(p, np.transpose(self.x))                  
        return np.transpose(y)

完整的程式碼已經push到了 Github, 歡迎star和fork。

後記

希望讀完本文對你有所幫助。

由於本人水平有限，文中難免有疏漏之處，還請大家批評指正。