一些定義

數論函式：定義域在正整數的函式

積性函式：\(\forall a\perp b,f(ab)=f(a)\times f(b)\)

完全積性函式：\(\forall a,b,f(ab)=f(a)\times f(b)\)

栗子

• 常數函式\[1(i)=1\]
• 么元函式\[e(n)=[n=1]\]
• 恆等函式\[id(n)=n\]

尤拉函式

\(\phi(i)\)表示\(1-i\)中與\(i\)互質的數的個數

引理：

• 如果\(n\)為素數p，\(\phi(n)=n-1\)
• 如果\(n\)為素數的次方，\(\phi(p^a)=(p-1)\times p^{a-1}\)
• 如果\(n\)為兩數之積，\(\phi(a\times b)=\phi(a)\times\phi(b)\)
• 若\(n=p_1^{a1} \times p_2^{a2}\times...\times p_k^{ak}\), \(phi(n)=n\times (1-1/p_1)\times (1-1/p2)\times ...\times(1-1/p_k)\)

尤拉定理

\(IF\ a\perp m,\ \ a^{\phi(m)}\equiv 1\ \ (mod\ \ m)\)

尤拉函式的線性篩法

• 性質1 \(\phi(p)=p-1\)
• 性質2 \(IF\ i\ mod \ p=0,\ \ (i*p)=p*\phi(i)\)
  
  證明
  \(\ \because n\)與\(i\)不互質，\(\therefore i\)與\(n+i\)不互質
  \(\ \because [1,i]\)中不與i互質的數有\(i-\phi (i)\)個，
  \(\ \therefore(i+1,p\times i]\)中一共有\(p\times \phi(i)\)個數\(\perp i\times p\)
• 性質3 \(IF\ i\ mod\ p\neq0,\ \ (i*p)=(p-1)*\phi(i)\)

調和級數

\[1+\frac 1 2+ \frac 1 3 + \frac 1 4 + ...\approx ln\ n\]

除數函式

\[\sigma _k(n)=\sum_{d|n}d^k\]
\(\sigma_0\)表示因子個數
\(\sigma_1\)表示因子和
積性函式

狄利克雷卷積

\[f*g=h\]
\[h(z)=\sum_{x*y=z} f(x)*g(y)\]
有交換律和結合律
如果\(f,g\)都是積性函式，\(h\)是積性函式

• 驗證卷積
  \[h(p^k)=\sum_{i=0}^kf[(p^i)\times g(p^{k-i})\]

栗子

• \(\varphi*1=id\)即\(\sum_{d|n}\varphi(d)=n\)

給定\(f,g\),求卷積前n項的做法-->暴力\(O(n\ ln\ n)\)

莫比烏斯函式

\[n=p_1^{k_1}\times p_2^{k_2}\times p_3^{k_3}\times .. \times p_m^{k_m}\]
\[if\ squarefree\ \mu(n)=(-1)^m\](就是說每一項的係數都是一次)
\[otherwise\ \mu(n)=0\]

\[\mu(n)=\mu(p_1^{k_1})\times \mu(p_2^{k_2})\times ...\times\mu(p_m^{k_m})\]

積性函式，但不是完全積性函式
\[\sum_{d|n} \mu(d)=[n=1]\]可改寫為\[u*1=e\]

證明：

\[n=p_1^{k_1}\times p_2^{k_2}\times p_3^{k_3}\times .. \times p_m^{k_m}\]

\[n_0=p_1\times p_2\times p_3\times .. \times p_m\]

\[\sum_{d|n}\mu(d)=\sum_{d|n_0}\mu(d)\]

當\(p_1\perp d\) ,\[\mu(dp_1)=\mu(d)\times\mu(p_1)=-\mu(d)\]

\[\sum_{d|n}\mu(d)=\sum_{d|n_0}\mu(d)=\sum_{d|\frac{n_0}{p_1}}(\mu(d)+\mu(dp_1))=0\]

線性篩法

void Linear_Shaker(int n)
{
    mu[1] = 1;
    for (int i = 2; i <= n; i++)
    {
        if (!ism[i]) {prm[++tot] = i; mu[i] = -1;}
        for (int j = 1; j <= tot; j++)
        {
            int num = prm[j] * i;
            if (num > n) break;
            ism[num] = 1;
            if (i % prm[j] == 0) break;
            mu[num] = -mu[i];
        }
    }
}

莫比烏斯反演

\[g=f*1\]

如果知道\(f,1\)直接求就行了啊

但是如果只知道\(g,f\)呢

反演！！！

\[g=f*1\]

\[g*\mu=f*1*\mu\]

\[g*\mu=f*e\]

栗子

• YY的gcd

  

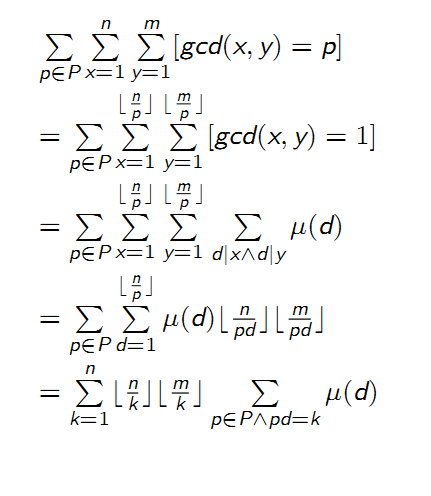
  \[g(k)=\sum_{p\in P\wedge pd=k}\mu(d)\]

  \[f(p)=[p\in P]\]

  \[g(k)=\sum_{pd=k}\mu(d)*f(p)\]

  預處理卷積！！

  然後每組詢問的答案變成\[\sum_{k=1}^{min(n,m)} \lfloor \frac n k \rfloor\lfloor \frac m k\rfloor g(k)\]

  \(\lfloor \frac n k \rfloor\lfloor \frac m k\rfloor\)只有\(O(\sqrt n)\)種取值

• 數表

  也就是說\((i,j)=\sigma(gcd(i,j))\)

  記\(f_a[d]\)表示\(gcd(i,g)=d\)的格子的貢獻

  \[f_a[d]=\left\{\begin{matrix}0,&\sigma(d)>a&\\ \sigma(d),&oterwise\end{matrix}\right.\]

  \[ans=\sum_df_a[d]\sum_k\mu(k)\lfloor\frac n{dk}\rfloor\lfloor\frac m {dk}\rfloor=\sum_t\lfloor\frac n t\rfloor\lfloor\frac m t\rfloor(\sum_{dk=t}f_a[d]\mu(k))\]

  把所有變數離線下來，每次修改改變的h複雜度\(O(n\ ln\ n)\)