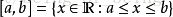1.1實數

1.1.1 集合

具有某種屬性的事務的全體成為集合

集合的表示方法：1）列舉法（列出每一個元素）；2）說明法（說明元素共有的特性，這種說明需要能概括所有的元素，且不能包含其他元素）。

1.1.2 實數集

（1）實數集R：

有理數集（R）+無理數集

（2）有理數特性：

1）有序性（任意兩個有理數可比較大小）；

2）對於加減乘除運算的封閉性（有理數通過四則運算得到的結果還是有理數）；

3）稠密行（任意兩個有理數之間至少存在一個有理數，也就是說，有無窮多個有理數）

（3）數軸：

1）有理數都可以表示為數軸上的點，但數軸上的點不一定是有理數；

2）數軸可以表示所有實數，包括有理數和無理數；

3）實數集具有完備性（連續性）。

1.1.3 區間

（1）有界區間

（2）無界區間

（3）鄰域

1）點a的δ鄰域：設δ是一個正數，則開區間（a-δ，a+δ）稱為點a的δ鄰域，記作

2）去心鄰域：只考慮點a鄰近的點，不考慮點a，即考慮點集{x|a-δ<x<a∨a<x<a+δ}，稱這個點集為點a的去心鄰域，記為，即

1.1.4 不等式

（1）三角不等式：

（2）伯努利不等式：