自定義堆(1):實現最大堆
阿新 • • 發佈:2019-01-03
通過學習自定義堆,瞭解堆的資料結構。

本篇以最大堆為例。
底層依賴了自定義陣列, 參考:自定義陣列 中的 Array.java
所以,其時間複雜度分析:
| add |
O(log n) |
| extractMax |
O(log n) |
| replace |
O(log n) |
對 siftUP方法的解釋:
每次將要新增的元素,放在陣列最後一個位置,按照最大堆的定義,使其值與父節點的值進行比較,決定是否“上浮
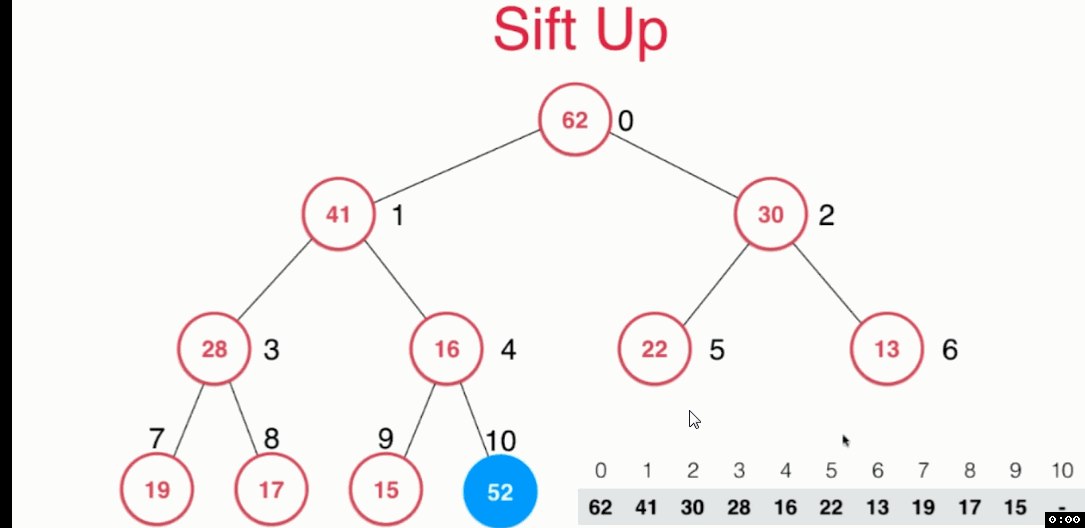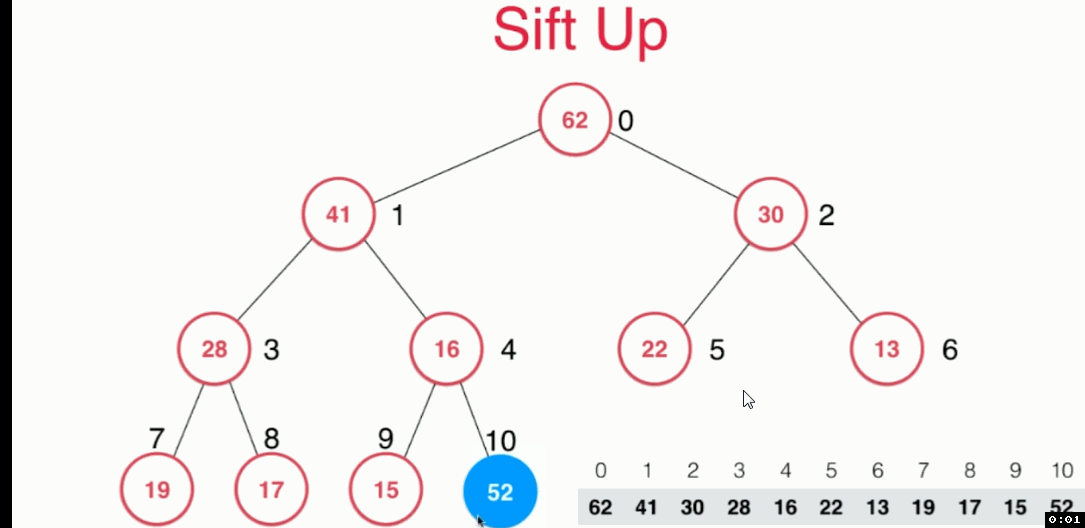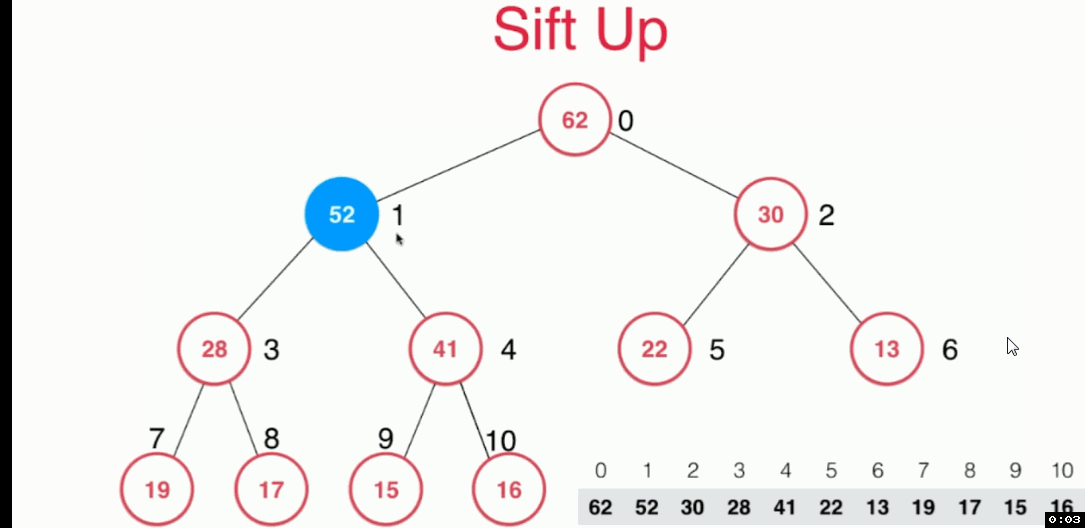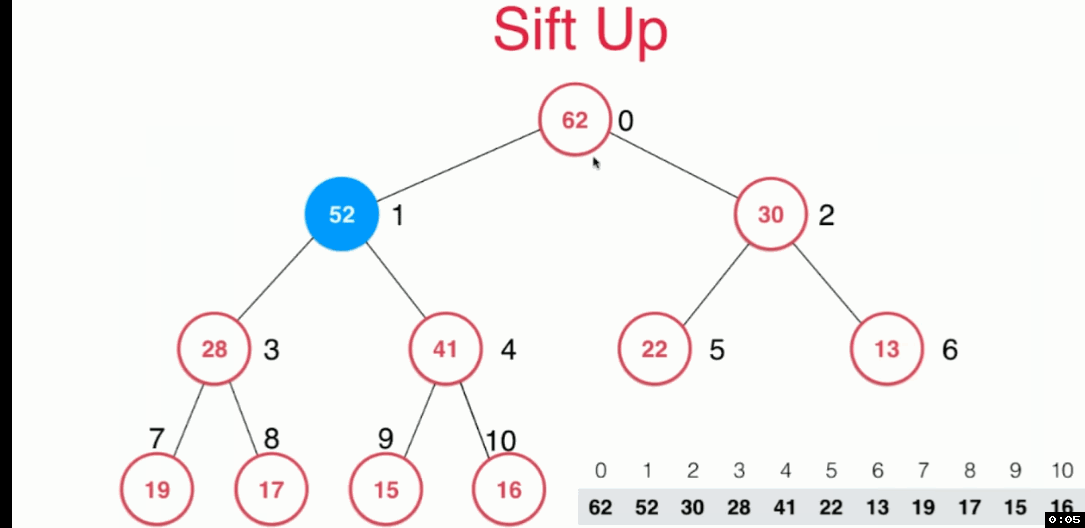
對siftDown方法的解釋:
將位於陣列最後位置的元素與最大元素交換位置,並刪除最大元素,對此時處於最大元素位置的元素,安裝最大堆的定義,比較其值與左右孩子中最大的那個的大小,進行“下沉”。
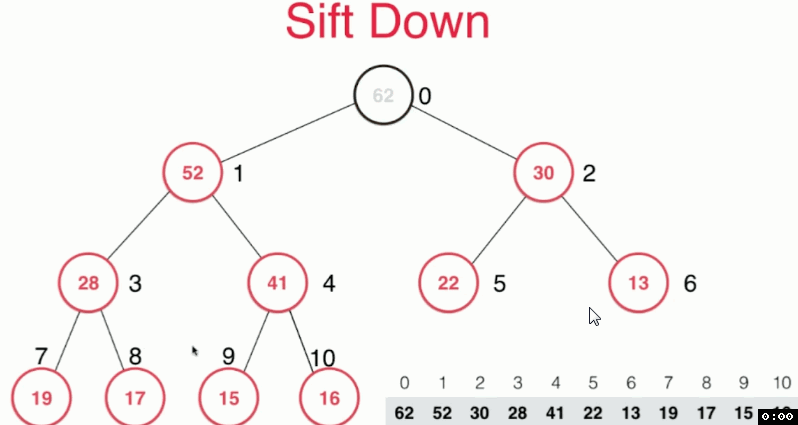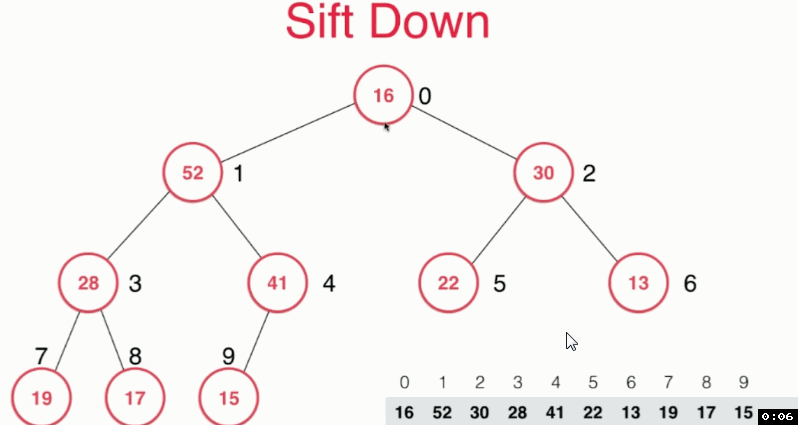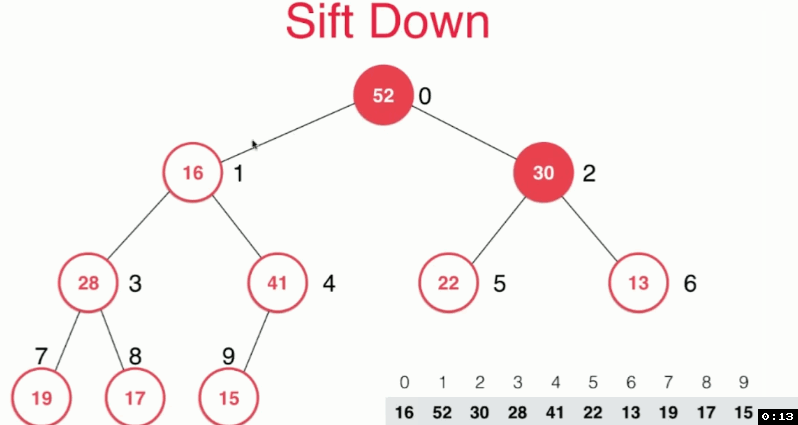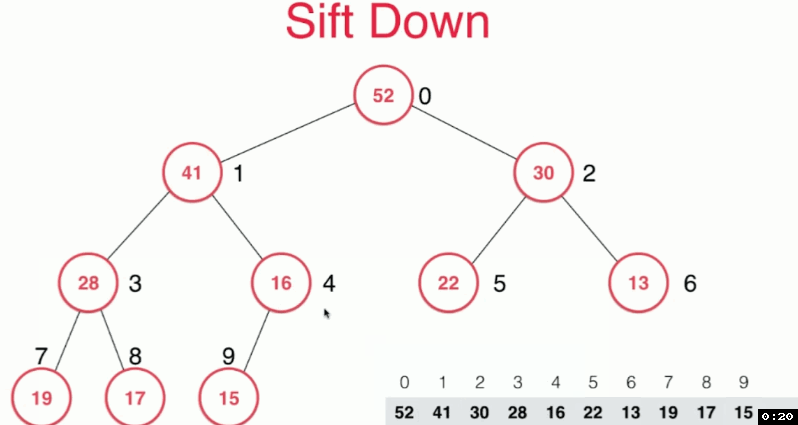
對replace方法的解釋:直接將堆頂元素替換以後sift Down。
Array.java 新增了一個方法:
/** * 新增 * 用於交換兩個位置的值 * @param i * @param j */ public void swap(int i,int j) { if(i < 0 || i >= size || j < 0 || j >= size) { throw new IllegalArgumentException("索引不合法"); } E e=data[i]; data[i]=data[j]; data[j]=e; }
MaxHeap.java:
package Heap; public class MaxHeap<E extends Comparable<E>> { private Array<E> data;//維護一個自定義陣列 /** * 帶參構造方法 * @param capacity */ public MaxHeap(int capacity) { data =new Array<>(capacity); } /** * 無參構造方法 */ public MaxHeap() { data=new Array<>(); } /** * 返回堆中的元素個數 * @return */ public int size() { return data.getSize(); } /** * 判斷堆是否為空 * @return */ public boolean isEmpty() { return data.isEmpty(); } /** * 返回完全二叉樹的陣列表示中,一個索引所表示的元素的父親節點的索引 * @param index * @return */ private int parent(int index) { if(index==0) { throw new IllegalArgumentException("索引為0,沒有父節點"); } return (index-1)/2; } /** * 返回完全二叉樹的陣列表示中,一個索引所表示的元素的左孩子節點的索引 * @param index * @return */ private int leftChild(int index) { return index*2+1; } /** * 返回完全二叉樹的陣列表示中,一個索引所表示的元素的右孩子節點的索引 * @param index * @return */ private int rigthChild(int index) { return index*2+2; } /** * 向堆中新增元素。 * @param e */ public void add(E e) { data.addLast(e); siftUp(data.getSize()-1); } private void siftUp(int index) { while(index>0 && data.get(parent(index)).compareTo(data.get(index))<0) { data.swap(index, parent(index)); index=parent(index); } } /** * 檢視堆中的最大元素 * @return */ public E findMax() { if(data.getSize() == 0) { throw new IllegalArgumentException("堆為空"); } return data.get(0); } /** * 取出堆中最大元素 * @return */ public E extractMax() { E e=findMax(); data.swap(0, data.getSize()-1); data.removeLast(); siftDown(0); return e; } private void siftDown(int i) { while(leftChild(i)<data.getSize()) { int k=leftChild(i); if(k+1<data.getSize()&& data.get(k+1).compareTo(data.get(k))>0) { k++; } //此時,data[k]是leftChild和rightChild中最大值 if(data.get(i).compareTo(data.get(k))>=0) { break; } data.swap(k, i); i=k; } } /** * 取出堆中最大的元素,並且替換成元素e * @param e * @return */ public E replace(E e) { E ret=findMax(); data.set(0, e); siftDown(0); return ret; } }
