一.揹包問題

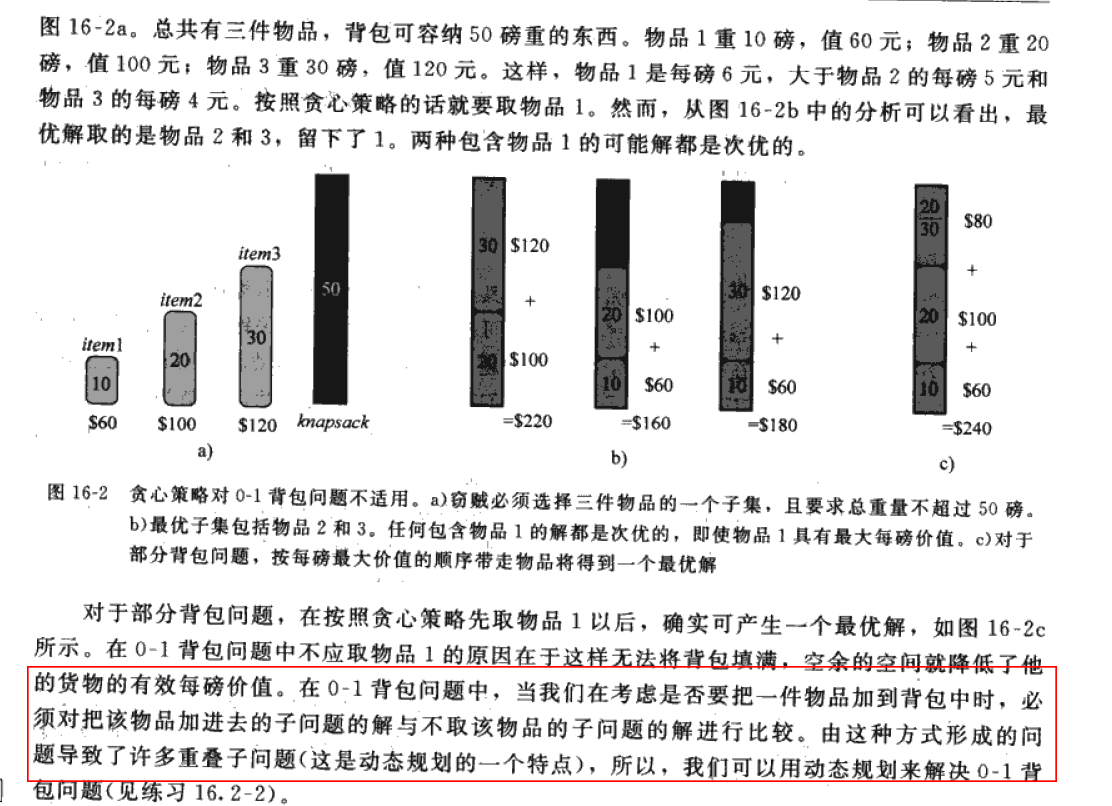
引用書上關於0-1揹包和部分揹包的闡述：

二.貪心與動態規劃區別

關於紅色矩形部分解釋為什麼0-1不能使用貪心演算法，是因為當你選擇一個物品時，整個物品的大小都需要計算，然而揹包的的大小又是固定的，那麼剩下的揹包大小與剩下的物品之間就有個容納問題。就像圖b第二個樹狀圖屬於容量20，而剩餘物品大小30，顯然放不下，所以說選擇放與不放會影響後放物體能否儘可能填滿揹包。這個與部分揹包問題不同，部分揹包問題，只要選擇從價值高到低放就能夠鐵定填滿，它的填放會影響價值，但是不會影響揹包能否填滿。
可以把0-1揹包想成往一個杯子裡放幾種固定大小鐵塊（但是沒有極其小可以用來填補空缺的）。
可以把部分揹包想成往一個杯子裡放粉末。先放石子，再放沙，最後水。

三.0-1揹包動態規劃問題

部分揹包很好理解，接下來說一說關於0-1揹包問題。在參考別人答案後，我想了好多關於遇到這種問題，我們該以何種順序，如果抓住問題解題關鍵點。

例子：5個物品，（重量w，價值v）分別為：（5，12），（4，3），（7，10），（2，3），（6，6）。

1、假設問題答案
　　我們共有5個物品，答案可以是（1表示取，0表示棄）：00011或者10101或者11000等等。不過不要用1，2，3，4，5代表物品，再用15或者123或者345表示答案。你會發現如果你只考慮取的部分不考慮棄的部分 ，問題答案位數一直不是固定的，增加難度。
２、假設最優答案
　　我們假設最優答案為00011。這樣根據動態規劃要求，考慮最優子問題。一般考慮子問題都是減少問題包含元素數量，同時保持子問題與原問題屬於同種問題，只是考慮數量減少了。比如我們減少第五個揹包。那我們的問題變成了什麼？這裡考慮極其特殊情況，除去的是最後一個物品。

例子：4個物品，（重量w，價值v）分別為：（5，12），（4，3），（7，10），（2，3）。

3、找到原問題與子問題之間聯絡
　　當00011為原問題最優解，那麼0001為子問題最優解。為啥？如果0001不是子問題最優解，假設0101為子問題最優解，那原問題最優解就是01011或者01010。與我們假設相悖。
　　那麼從子問題到原問題要經過什麼樣考慮？我們現在已經找到子問題最優解，到原問題解我們只需考慮第五個物品是取還是棄？如果取，那麼取以後揹包空餘量減少，揹包價值增大；如果棄，揹包價值也會變化，因為此時我們揹包容量變大了，那麼我們先前的取法就有可能需要改變。所以我們需要在這裡進行判斷。
　　如果一個問題的最優解包含了物品n，即物(n)=1，那麼其餘物1，物2，…，物(n-1)一定構成子問題1，2，…，n-1在揹包容量W-w(n)時的最優解。如果這個最優解不包含物品n，即物n=0，那麼其餘物1，物2，…，物(n-1)一定構成子問題1，2，…，n-1在揹包容量W時的最優解。
4、迭代公式的建立

　　首先我們需要考慮是什麼可以讓我們把問題拆分成子問題？在矩陣鏈中我們是根據矩陣鏈中擁有的矩陣Ａ個數來拆分的。通過縮小矩陣個數變成子問題。那麼在0-1揹包中是否也可以減少個數呢？答案是不一定。假設我們現在考慮選取兩個物品，我們是可以直接選擇兩個價值和最大物品。但是還有一個因素：重量和問題。在重量和不等情況下認為價值和最大的兩個物品總價值最大。顯然這是不公平的。所以這裡我們需要考慮兩個因素：一個是物品數量，另一個是揹包容量
　　再考慮一下我們問題的變數有哪些？這個地方考慮的只是變數變化的一個相對關係。
　　揹包物品i 　　揹包當前擁有價值tab 　　揹包當前重量j
0 　　　　　　　0　　　　　　　　　　 0
1　　　　　　　 12　　　　　　　　　　5
2 　　　　　　　12+3=15 　　　　　　5+4=9
……
可以看到我們新增一個物品，揹包價值增加，揹包重量增加。
根據步驟3中我們可以發現：
　tab(i+1) = max( tab(i) + v(i+1) , tab(i) )
　j(i+1) = j(i) + w(i+1) 或者 j(i) 此處變化跟上一個公式對應。
目前的話我們有兩個變化公式，在迭代中我們將其轉化成一個：

tab[i][j] = max(tab[i-1][j-weight[i]]+value[i],tab[i-1][j]) ({i,j|0< i <=n,0<= j <=total})

5、例題解析過程
　　到第4步，我們已經完成問題的思考，接下來看一下，例題的思考過程，加深理解。

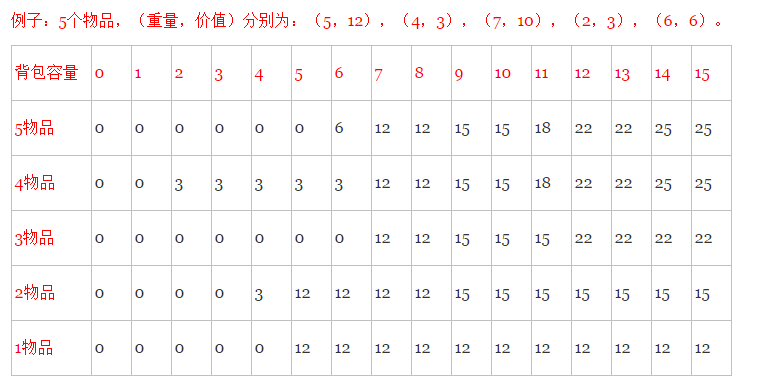
　　看圖片中表格第一行，我們就是通過控制揹包容量來控制子問題大小。隨著揹包容量增加，能夠容納更多物品，逐漸擴大，最後直至達到問題揹包容量。
　　當i=1時，只能選一個1物品，看1物品行（表中第六行），隨著揹包容量增大，揹包可以放得下1物品
　　當i=2時，可以選1物品和2物品，當揹包容量增大至4時，此時我們可以選擇2物品價值為3；繼續增大揹包容量，當揹包容量增大至5時，我們可以不放2物品放1物品，價值為12；當揹包容量為9時，1物品2物品都可以放得下，兩個都放，價值15。
　　。。。。。。
　　看下迭代公式：
　　tab[i][j] = max(tab[i-1][j-weight[i]]+value[i],tab[i-1][j]) ({i,j|0< i <=n,0<= j <=total})
　　當決定是否放入i時，我們需要考慮兩種子問題。
　　一：如果放入，那我們考慮在物品數為i-1， 揹包容量為j-weight[i]時的價值
　　二：如果不放入，物品數為i-1， 重量為j時的價值
　　哪一個大，選擇哪一個。