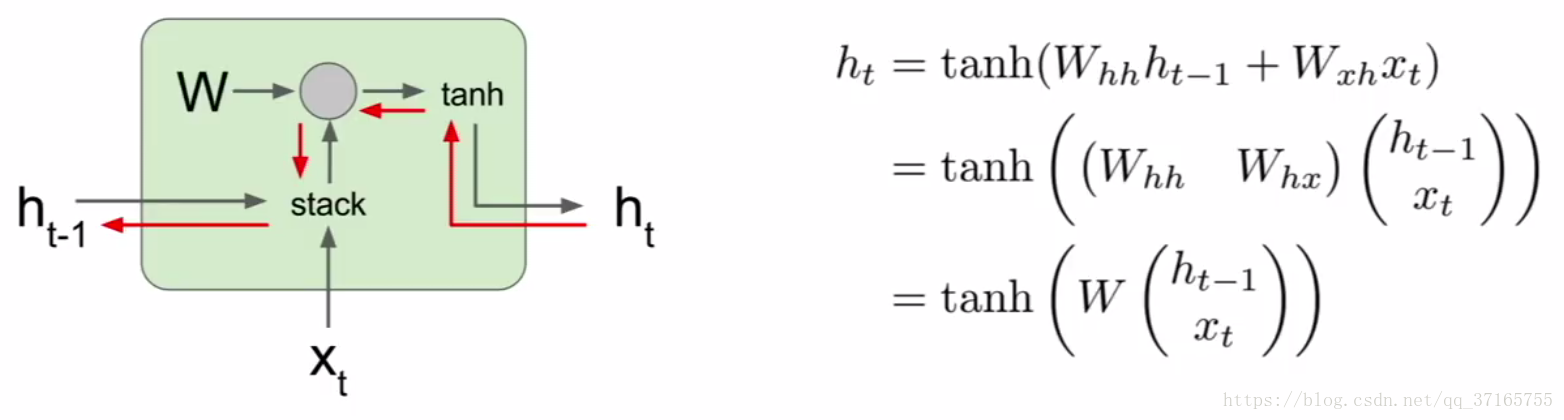卷積神經網路 + 機器視覺: L10_RNN_LSTM (斯坦福CS231n)
完整的視訊課堂連結如下:
完整的視訊課堂投影片連線:
前一課堂筆記連結:
RNN 是一個包含非常廣泛的應用領域與知識範圍的一大門類,他的全名又叫做 Recurrent Neural Network,也是神經網路的一種,但是差別就在於 RNN 讓神經網路中的節點(node)在運算的時候,還參考了“歷史資訊”,能夠見往知來的貫通所有節點的訊息,並通過新資料與歷史資料的彼此關係和出現順序來預測下一個 output 的結果。
雖然上述說得輕描淡寫,但是為了達到以上效果,有許多架構與方法必須被套用到其中,很多內容超出了 Stanford CNN 課程的範疇,我一併整理在了下文,後續持續開新篇幅針對介紹。歷史資訊與序列的先後引發的延伸應用是一種不同維度的躍進過程,但凡有先後性的資料,都可以跟 RNN 拉上關係,例如:文字,影片,聲音,甚至是股票資訊。
文字又包含了描述語句,新聞搞,論文,摘要,評論分析,書面翻譯等等數不清的分項應用。影片類似道理也包含了物件互動關係,行為意義,肢體語言等。聲音則像是語音識別,語義識別,語音翻譯等。如果這三大類做 C3取 2 的排列組合,那還有一堆夢幻般的應用場景值得挖掘。
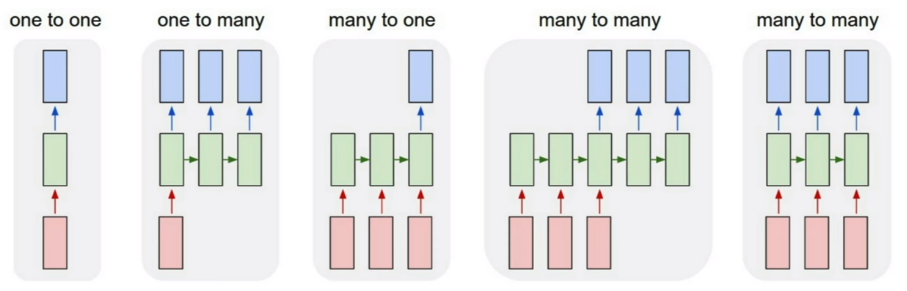
RNN 執行順序 (Process Sequences)
上圖中一共有 4 種 case,按照順序說下來的用法即為:
- Vanilla Neural Networks,一進一出(最簡單的形式)
- Image Captioning,一進多出(給一張圖,用文字描述內容)
- Sentiment Classification & Video Recognition,多進一出(連續動作判斷行為歸屬)
- Machine Translation between Languages,多進多出(翻譯工作)
Introduction paper link: Connectionist Temporal Classification (CTC)
加上歷史資訊這個維度帶給我們的優勢是不可言喻的,時間串起了世界的運轉走向,很多事務只有時間維度的參與,其本質與意義才能夠被賦予,RNN 最大的優勢莫過於此,綜合了龐大的電腦運算能力與資料資料,讓多個維度的考量成為了可能。
2014 年底新提出的一篇論文 Neural Turing Machine,可以把 model 自己新學到的東西放入到 Machine's Memory 裡面做新一輪的迭代。
The Composition of Modern RNN
- Input data
- Hidden RNN layers
- Memory functionality
- Selecting logic
- Output data
這個架構又叫做 LSTM 的架構,因為最簡單的 RNN model 在作為深層的神經網路的時候是有許多問題存在的,為了解決問題並且同時保有原本的 RNN 效能,LSTM 因應而生,這個 model 也因此已經成為了 RNN 的代名詞,基本上沒有人在用最簡單的 RNN model 去訓練資料了。
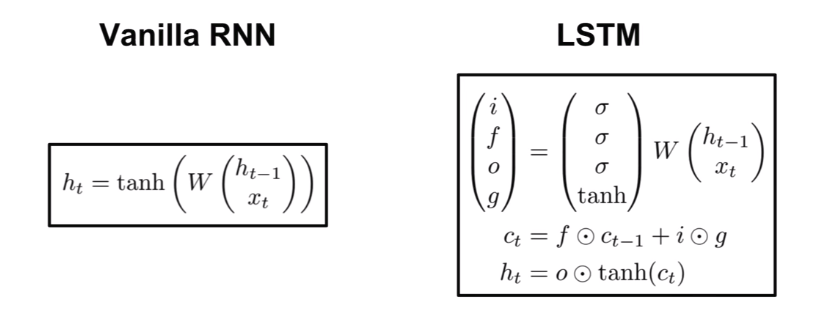
但是為了透徹理解 RNN 原理,還是必須回顧到最簡單的 model 上,一步一步的一窺究竟。一進一出的 case 種,公式如下:
代數說明:
t - 表示位於 t 的時間點,t-1 就是上一個單位的時間點
h - 表示 hidden layer 的內部執行機制
W - 表示權重,後面跟著兩個小代數先表明哪個引數的,再表明哪個方程的
x - 表示 input data
y - 表示 output data
把當下的 x 還有上一次運算好的 hidden layer 裡面的結果作為兩個 input 代入新的 hidden layer 裡面,這個 hidden layer 裡面的機制是個 tanh function,運算出來後再乘上一個 W 作為 output 輸出,這麼一來就把歷史資訊也一併考慮進去了。如果把這個機制作為一個 unit 把很多歌同樣的 unit 串起來,結果就會是如下圖:
可以看出來 W 是一個回收再利用的引數不斷的被重新放入下一個時間點的 unit 裡面,並且同樣的 W 在 RNN 裡面也是要被訓練的,每次 output 出來後會根據標準資料得出一個 loss value,同樣藉由 Gradient Descent 還有 Backpropagation 的方法,把 loss 值降到最低,逼出最優狀態。為了提升準確率,RNN 甚至可以是雙向的過程,又稱為 bidirectional RNN。真正意義上做到 “鑑往知來” 的境界。
RNN 的架構其實有兩個些微不同的版本,分別叫做 Elman 和 Jordan Network,差別就在於歷史資訊的儲存方式不同,Elman 是把 hidden layer 的結果作為下一層 network 的輸入迭代,反觀 Jordan 則是把整個 unit 的 layer 輸出作為下一個 unit 的輸入,就結果而言其實差異不大。
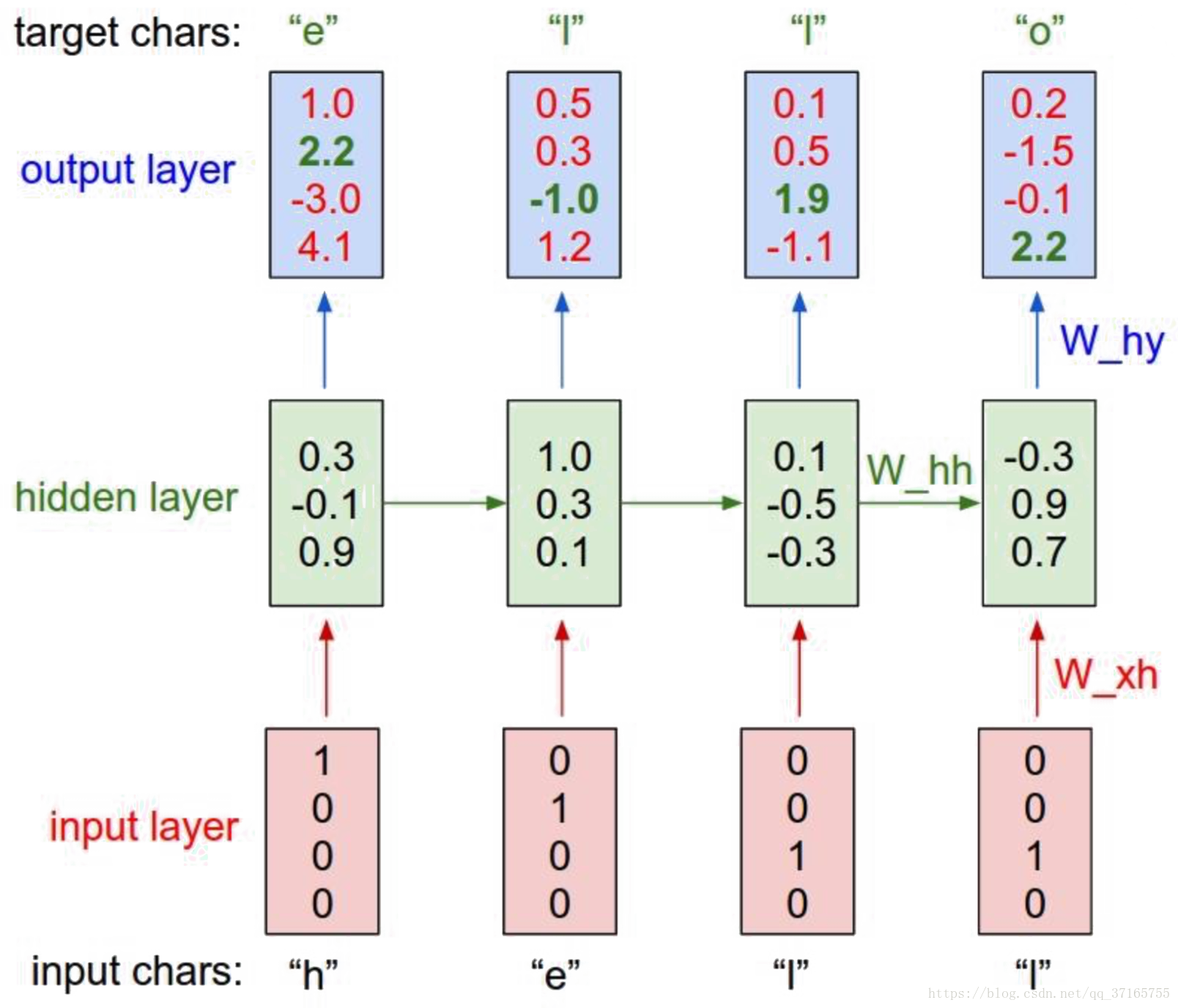
用 RNN model 測試簡單的 文字順序問題的話,實際案例如下:
如果希望 RNN 能夠拼出 “hello” 這個字,那麼我們就要設計每個字母后面出現下一個字母的可能性有多少,例如上例中,h 後面出現 e 的可能只有 2.2, 但是出現 o 的可能卻是 4.1,顯然是一個不合格的狀態,因此經過 loss function 得出來的值應該會很大,需要繼續使用 GD 去優化引數,並使得最後結果能夠儘可能地貼近我們的預期。
RNN Gradient Flow
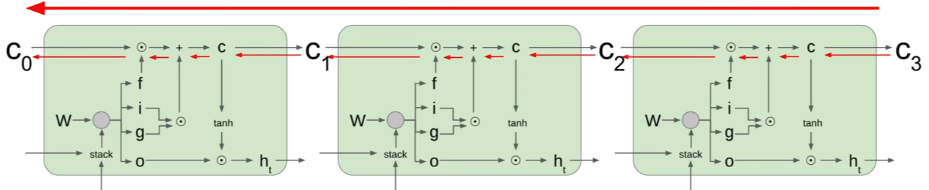
梯度流視覺化過程與對應的共識如下:
先是一個數據和歷史資訊與 W 的 dot product 過程,再把結果放到 tanh 裡面加工,得出一個 output,dot 的微分做起來相對輕鬆,但是 tanh 就不是那麼好說話的角色了,佔用資源的 tanh 和會消失或爆炸的 W 使得這個 model 有無盡的瓶頸。
暫時的方法:Gradient Clipping,程式碼如下:
grad_norm = np.sum(grad * grad)
if grad_norm > threshold:
grad *= (threshold / grad_norm)
用一個判斷式阻斷梯度通往爆炸或是消失的途徑,但是斬草不除根的情況下這個方法還是被詬病的。這個初階的 model 有著無可避免的痛點,隨著神經網路的深度增加,劣勢暴露的更加明顯,有兩個原因導致初階版本的神經網路癱瘓:
- tanh 的反向傳播計算是個佔用資源的過程,tanh 中的 tanh 中的 tanh... 迴圈下去的微分更是一個龐大的計算負擔
- 梯度爆炸或是消失 Gradient Exploding or Vanishing,這裡不像 CNN 裡面有 Batch Normalization 等緩解此症狀的機制,在傳遞誤差的時候更無可能不斷延伸,即便 W 是 1.1 到後來也是爆炸收場,0.9 也是消失結束
tanh 在使用上更為符合我們的預期,效果也更好,作為一個 activation function 的存在是不可被替代的,而 BN 是用在 data 上的方法,也不是直接套用在 W 上的,在這兩個問題沒辦法被側面繞開的情況下,聰明的人腦還是想出了因應之道。
Truncated Backpropagation
第一招就是減負。隨著深度增加,運算量成了負擔,因此我們就選擇只 BP 到一定的深度即可,如要計算第 100 層的梯度,就選前 50 層去做 BP 然後剩下的部分就不管了,同理其他層節點的梯度運算,這個方式類似 Mini-Batch 的邏輯,可以大幅減少計算成本,從經濟效益來看,損失一些精確度換來時間,非常划算。
第二招就是重構整個 model,也就是 LSTM 誕生的原因,介紹前先更深入的理解 simple model 出問題的癥結點。
Long Short-Term Memory (LSTM)
這個方法早在 1997 年就已經被髮明使用,它把原本簡單的 model 內容增加了更多東西,如最一開始介紹的 RNN 結構,含有記憶門,遺忘門,選擇門等通道,更加細緻的過濾問題。不過這個章節中 Stanford 課說的並不夠完整和易懂,兩篇補充文章值得一讀:理解 LSTM 網路(點選) & RNN 及 LSTM 的介紹和公式梳理(點選)。
並且仔細上了一位臺灣大學教授李巨集毅的線上課程 part1 與 part2 後,終於能夠初步完整的繼續撰寫此文,順利為我填補了 Stanford 留下來的知識空缺(發自內心的感謝大神老師)。顧名思義,其實它就是一個 “長了一點” 的短期記憶演算法架構,擁有多個掌管不同部位的 Gate 去控制資料的 “流” ,經過 Gate 的篩選,讓有意義的 data 被留下,而是否有意義這件事情,則是 machine learning 重要的一環。(這些圖片中也使用到了李老師提供的 PPT,只為更好的詮釋內容)
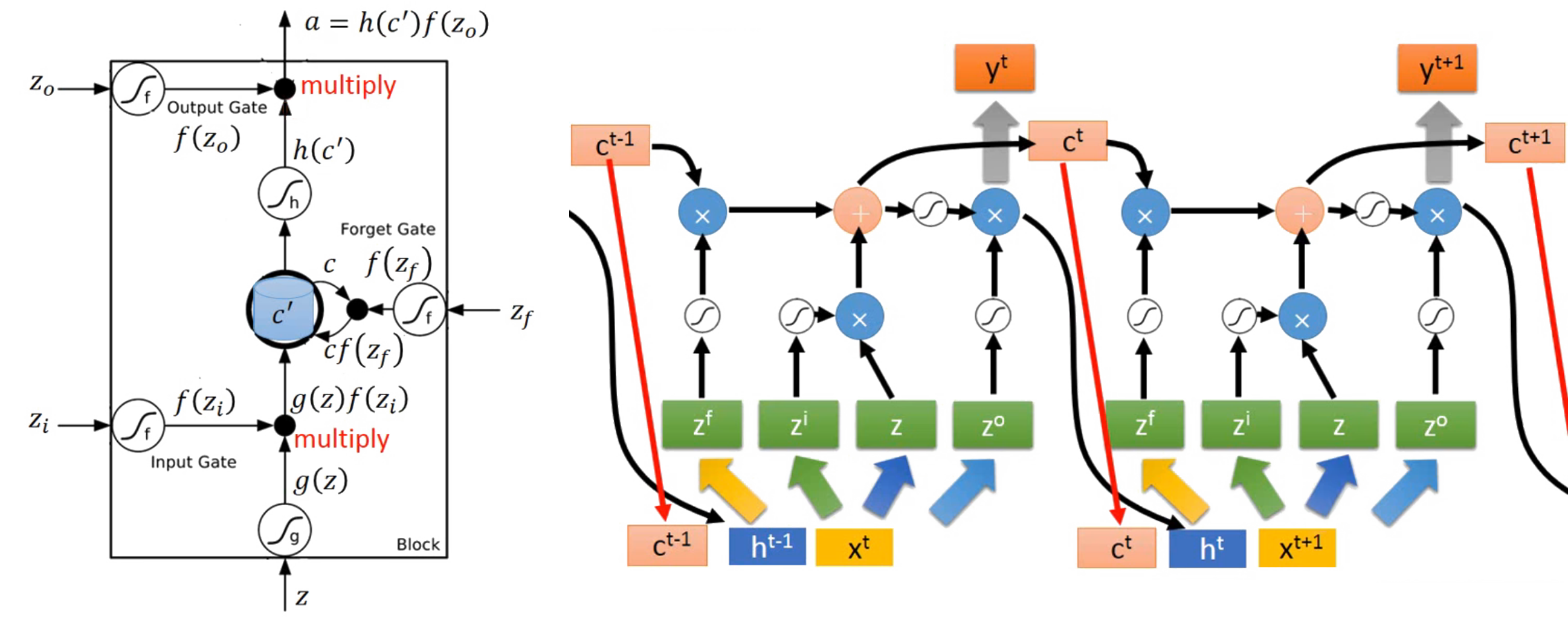
影象中建構好了架構後,接下來就是把架構數學化,最後再把數學轉換成電腦可執行的程式碼,等看到結果符合預期當下,最激動人心的剎那莫過於此了! Gate 無非就是一個 “是與否” 的判斷,使用 Sigmoid function 非常恰當。LSTM 的組成有: input gate, forget gate, output gate, Memory cell 四個部分。
有別於前面幾節課記錄的內容,一般 Neural Network 的 input 只有一個對應的處理通道,那就是乘以 Weight 加上 bias 之後把結果塞進 activation function 裡面得到一個神經 unit 的輸出結果,並以此結果作為下一層神經 unit 的 input 不斷迭代。然而對於 RNN 的 LSTM model 而言,input data 卻需要塞到到四個對應不同權重 Weights 的通道之中作為資訊源,提供個別通道的學習方向,這四個通道分別是:input data, input gate, forget gate, output gate。
如上流程圖,所有的 Gates 都是一種 activation function 參與,以下分別說明:
- input data, position of z
首先用同一個 fed in data 乘以屬於這個 gate 專屬的 Weight,再加上屬於這個 gate 的 bias,然後把結果送進 activation function 裡面,結束這回合的任務,留下結果 g(z),等待著與下一個 gate 輸出的結果會合。 - input gate
首先用同一個 fed in data 乘以屬於這個 gate 專屬的 Weight,再加上屬於這個 gate 的 bias,然後把結果送進 activation function 裡面,得出結果 f(zi) 會識別出哪些新進的 data 可以通過於此,並與剛留下的結果 g(z) 相乘,把有 “通行證” 的 data 送往記憶門與舊的 data 相會。 - forget gate
首先用同一個 fed in data 乘以屬於這個 gate 專屬的 Weight,再加上屬於這個 gate 的 bias,然後把結果送進 activation function 裡面,的出結果 f(zf) 會識別出哪些舊的 data 可以被繼續保留,而哪些該忘記,並與上回合留下來的記憶集 c 相乘,把有 “拘留權” 的 data 喚出並相加結合,結果就是:g(z) * f(zi) + c * f(zf) = c' 。 - memory cell
作為握有通行證與拘留權者的集合地出發,但是注意這邊是沒有專屬的 Weight 要被相乘的,直接集合後送進 activation function 得出一個結果 h(c'),並且等待 “放行證” 的領取。該回合存活於此的 data 則會繼續在下回合作為舊的 data 通過 forget gate 執行新一輪的篩選。 - output gate
首先用同一個 fed in data 乘以屬於這個 gate 專屬的 Weight,再加上屬於這個 gate 的 bias,然後把結果送進 activation function 裡面,得出的結果 f(zo) 就是根據前面運算最後的出來放行證的 “張數” ,最後用相乘的方法: h(c') * f(zo) 把證發給指定的資料順利輸出,並作為下一次要輸入的一部分。
在實際寫程式碼的時候,四個 gates 對應到的不同 Weights 會作為不同的 vector 互補干涉的獨立存在,並且 vector 裡麵包含不同 dimension 的元素就是根據每層同一個 input 位置的多寡而定,每次每層的 unit cell 輸入的運算元素都只是這些總的 vector 其中一個 dimension 的東西。所以 RNN 跟別的神經網路最大的差別就是其 input data 要被放入 4 個地方做不同的處理,並把個別處理出來的元素再彼此相加相乘和 activation function 攪在一起,而不像之前不含時序問題的 NN 一般,一個 input data 對應到一個地方處理完後就可以了,也因為如此,LSTM 的引數量是一般 NN (包含一般 RNN) 所需的 4倍。
Peephole
實際應用中,除了本身新的 data 和歷史 data 作為 input 端考慮外,還會把存在 memory cell 裡面的元素納入考慮範圍中,把這三個參考元素並在一起再去乘以四個藏在不同 vectors 裡面的 z 值。把 c‘ 也參考進來的這個動作就是 peephole 的精髓了(如上圖 ct 的遭遇)。
當然上面這些內容都是最底層的原理,實際在寫程式碼的時候,有個 python module called: keras 裡面直接涵蓋了上述內容的功能,只要一個呼叫就可以完事了,是個非常值得探索的工具!裡面還包含了 LSTM & GRU & SimpleRNN 三種模式,其中要屬 LSTM 最難,其他都是 LSTM 的簡化版本。但是第二招說明了那麼久,增加了那麼多繁瑣的細節,實際為了達到的功能還是要解決 Gradient Descent 在 SimpleRNN 沒辦法良好收斂的問題。
Backpropagation Through Time
但凡是神經網路,就離不開梯度下降與反向傳播這兩名大將的陪同,RNN 也不例外,不過相對於前面的 Neural Network 操作狀態,RNN 的訓練途徑並不是一路順歲的下降過程,原因是其 function 畫成視覺化的結果所呈現出來的崎嶇表面與陡峭地形,在訓練前就已經作為一個 Hyperparameter 被定死的 learning rate 要是遇到了踩在陡峭懸崖上的超大梯度,結果就是步距超大飛出了掌控範圍從此永遠別想收斂。
因此,Gradient Clipping 如上面的三行程式碼就是用來限制此一情況讓事情不發生,當 update 的值超過一定的大小時,就讓值等於我們能接受的設定範圍,並繼續下一迴圈。但是即便如此,Gradient Exploding or Vanishing 的問題還是存在於 SimpleRNN model 當中,隨著神經網路的層數加多,time sequence 裡面同樣的 Weight 值會不斷的重複使用,造成問題越來越嚴重,所以同樣需要 LSTM 來拯救。
Memory Cell
相較於一般的 model,LSTM 多了一個 memory cell 的構造,並且與其直接按照原來的計算路徑反推出 Backpropagation 的結果,取而代之的是讓 Backpropagation 去計算 memory cell 的梯度,不但繞開了 tanh 的繁重資源佔據問題,且梯度計算的值只是 matrix 裡面其中一個(或是幾個)元素(影片裡面稱作:elementwise multiplication),而不是 full matrix multiplication 這種比較不好的出結果的情況。LSTM 裡面的 cell state 就如同提供了 GD 在計算的時候一個高速公路,可以快狠準的朝向目標前進。
可以這麼做的原因就在於,每一個 LSTM 的 output 都是 “該回合的 input + 當時還記得在 Cell 裡面的 data”,所以可以直接從 Cell 著手去影響整個 network output 的輸出。
But here is an exceptional case written in one published paper: Vanilla RNN initialized with Identity matrix + ReLU activation function. The main point is that SimpleRNN model can easily beat back LSTM model by initializing with Identity matrix and using ReLU activation function.
直到現在,很多 RNN 的 model 都還是基於 LSTM 的原理去改進,會有些微的優化,但是整體而言並沒有大幅的效能提升。
下節連結: