使用異或運算實現兩數交換
通常我們實現兩數交換不得不引入一個臨時變數temp作為媒介,而使用異或運算也能實現同樣的功能,甚至無需使用臨時變數。
這是一個通常的做法:
int main(){
int a=1,b=2,temp;
temp=a;
a=b;
b=temp;
printf("%d,%d\n",a,b);
return 0;
}關於異或(Exclusive OR)
Wikipedia解釋
在數位邏輯中,邏輯算符互斥或閘(exclusive or)是對兩個運算元的一種邏輯分析型別,符號為XOR或EOR或⊕。與一般的或閘OR不同,當兩兩數值相同為真..而有一數值不同時為否..
兩個運算元(命題):A與B的異或一般寫成A異或B,或者寫成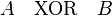
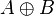 、
、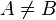 等等。在C語言中,寫作A^B。
等等。在C語言中,寫作A^B。
兩個相同數的異或結果為0
異或真值表
| A | B | A^B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
異或的小例子
假設a為二進位制數01,b為二進位制數10,a^b的結果為11並將其儲存在變數c中,經過反覆的測試,於是發現以下的規律:
11^01=10
11^10=01c^a=b;
c^b=a;原理很簡單,兩數異或的結果儲存了兩個數上每一個二進位制位不同或相同的資訊,如果相應的二進位制位不同,就標誌為1,如果相同,則標誌為0。
由於任意一個二進位制位與1異或有這樣一個特性:
0^1=1
1^1=0這樣,我們就使用異或運算交換了兩數
12(001100)
^ 34(100010)
-------------------
101110
101110 ^ 001100=100010
101100 ^ 100010=001100
int main(){
int a=12,b=34,temp;
printf("Original result: a=%d,b=%d\n",a,b);
temp=a^b;
a=temp^a;
b=temp^b;
printf("Transformed result: a=%d,b=%d\n",a,b);
return 0;
}Original result: a=12,b=34
Transformed result: a=34,b=12
但是使用這種方法似乎與使用臨時變數沒有什麼區別?
其實不然,通過簡單分析可以發現臨時變數的值在整個過程中並沒有發生變化,因此也可以無需設定臨時變數。
a=a^b^a;
b=a^b^b;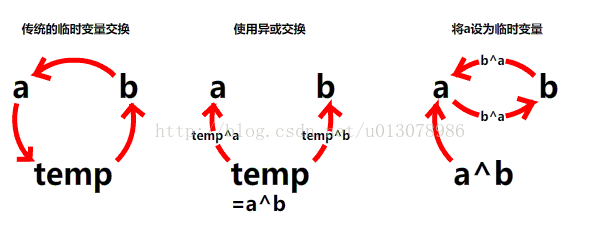
a=a^b;
b=b^a;
a=b^a;a^=b^=a^=b;還可以通過加減實現兩數互換:
a=a+b
b=a-b;
a=a-b;
前提是a+b的值不能溢位。
測試程式如下:
int main()
{
int a = 4, b = 5;
printf("a=%d b=%d\n", a, b);
a = a ^ b;
b = a ^ b;
a = a ^ b;
printf("a=%d b=%d\n", a, b);
}
執行結果:
[[email protected] cs]# ./a.out
a=4 b=5
a=5 b=4
[ 注意:當a和b相等時,該方法不適用]
其他方法:
public void change1(int a, int b){
System.out.println(“change1交換之前\ta:”+a+”\tb:”+b);
a = a + b – (b = a);
System.out.println(“change1交換之後\ta:”+a+”\tb:”+b);
} public void change2(int a, int b){//C/C++ 不適用
System.out.println(“change2交換之前\ta:”+a+”\tb:”+b);
b = a + (a = b)*0;
System.out.println(“change2交換之後\ta:”+a+”\tb:”+b);
} public void change4(int a, int b){
System.out.println(“change4交換之前\ta:”+a+”\tb:”+b);
a = a * b;
b = a / b;
a = a / b;
System.out.println(“change4交換之後\ta:”+a+”\tb:”+b);
}
