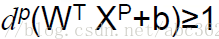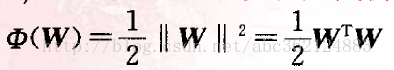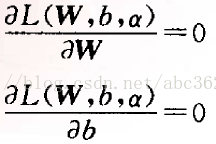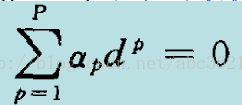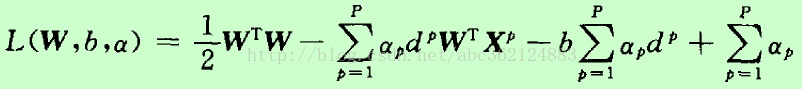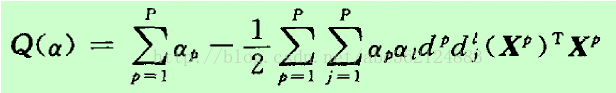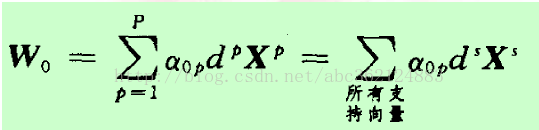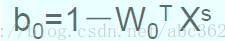一.簡介

        SVM主要針對小樣本資料進行學習、分類和預測（有時也叫回歸）的一種方法，能解決神經網路不能解決的過學習問題，而且有很好的泛化能力。SVM是一種有監督的學習模型，在處理二分類問題上可以說是現有演算法中的最好的一種。很多正統的演算法都是從VC維理論和結構風險最小原理出發，從而引出SVM，但是對於統計理論基礎不是很好的人來說理解起來比較困難，本文從線性可分情況開始，利用幾何知識和數學中的約束優化方法解決分類問題。然後引申到線性不可分的情況，再來理解基於內積核的最優超平面構造方法。希望有助於大家對演算法的理解。

二.線性可分情況下的SVM理解

        線性可分資料的二值分類機理：系統隨機產生一個超平面並移動它，直到訓練集中屬於不同類別的樣本點正好位於該超平面的兩側。顯然，這種機理能夠解決線性分類問題，但不能夠保證產生的超平面是最優的。支援向量機建立的分類超平面能夠在保證分類精度的同時，使超平面兩側的空白區域最大化，從而實現對線性可分問題的最優分類。

        支援向量機（Support Vector Machine，SVM）中的“機（machine，機器）”：實際上是一個演算法。在機器學習領域，常把一些演算法看作是一個機器（又叫學習機器，或預測函式，或學習函式）。

        “支援向量”：是指訓練集中的某些訓練點,這些點最靠近分類決策面，是最難分類的資料點 。

         “最優超平面”： 考慮P個線性可分樣本{(X1，d1)，(X2，d2)，…，(Xp，)，…(Xp，)}，對於任一輸入樣本Xp ，期望輸出為 =±1（代表兩類類別標識）。用於分類
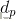
的超平面方程為
                                                                                                         

式中，X為輸入向量，W為權值向量，b為偏置（相當於前述負閾值），則有 

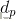
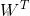
                                                         X+b>0   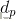                                =+1 

                                                                                                 X+b<0       

=-1

超平面與最近的樣本點之間的間隔稱為分離邊緣，用ρ表示。支援向量機的目標是找到一個分離邊緣最大的超平面，即最優超平面。也就是要確定使ρ最大時的W和b。如下圖

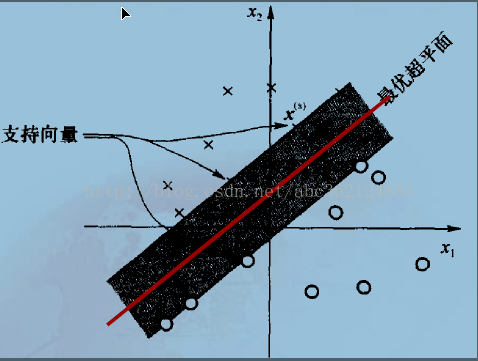
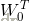
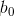
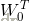
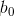
        可以看出，最優超平面能提供兩類之間最大可能的分離，因此確定最優超平面的權值和偏置應是唯一的。在式(1)定義的一簇超平面中，最優超平面的方程應為:X+=0（應該是X + = 0吧？ ）直接求和基本上不太可能，除了訓練集無別的資訊可用，如何辦？一種方法：使求得的預測函式 y = f(x) = sgn(W·X + b)對原有樣本的分類錯誤率最小。 如何使分類錯誤率最小？下面慢慢分析。

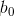
        由解析幾何知識可得樣本空間任一點X到最優超平面的距離為

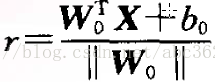
        從而有判別函式 :   g(X)=r ||W0||=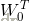X+
        g(X)給出從X到最優超平面的距離的一種代數度量。將判別函式進行歸一化，使所有樣本都滿足

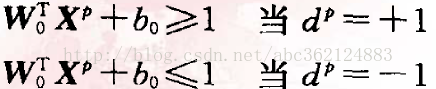
       上 式中的兩行也可以組合起來用下式表示

                                  （2）

         則對於離最優超平面最近的特殊樣本Xs滿足：I g(Xs) I=1，稱為支援向量。由於支援向量最靠近分類決策面，是最難分類的資料點，因此這些向量在支援向量機的執行中起著主導作用。

        可匯出從支援向量到最優超平面的代數距離為

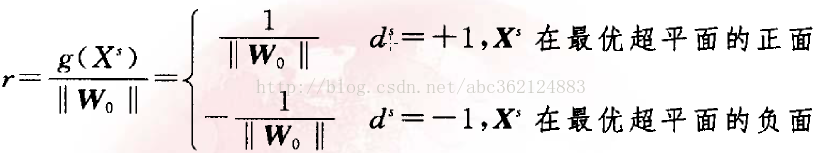
        因此，兩類之間的間隔可用分離邊緣表示為

       上式表明，分離邊緣最大化等價於使權值向量的範數|| W||最小化。因此，滿足式(2)的條件且使||W||最小的分類超平面就是最優超平面。

       建立最優分類面問題可表示成如下的約束優化問題，即對給定的訓練樣本{(X1，d1)，(X2，d2)，…，(Xp，)，…(Xp，)}，找到權值向量W和閾值B的最優值，使其在式(2)的約束下，有最小化代價函式 

        該約束優化問題的代價函式是W的凸函式，且關於W的約束條件是線性的，因此可用高等數學中Lagrange係數方法解決約束最優問題（即求解條件極值問題）。引入Lagrange函式如下

                      （3）

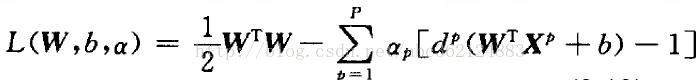
        式中αp≥0，稱為Lagrange係數。式中的第一項為代價函式 φ(w)，第二項非負，因此最小化φ(w)就轉化為求Lagrange函式的最小值。觀察Lagrange函式可以看出，欲使該函式值最小化，應使第一項φ(w)↓，使第二項↑。為使第一項最小化，將上式對W和b求偏導，並使結果為零

            可匯出最優化條件：

                                                                            （4）

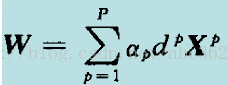
       為使第二項最大化，將式(3)展開如下

       將最優化條件代入上式整理得關於α的目標函式為Q(α) ＝L(W,b,α)

        以上為不等式約束的二次函式極值問題(Quadratic Programming，QP)。由Kuhn Tucker定理知，式(3)的最優解必須滿足以下最優化條件(KKT條件)

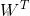
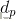
        上式等號成立的兩種情況：一是αp為零；另一種是 ( XP+b) =1 。第二種情況僅對應於樣本為支援向量。設Q(α)的最優解為{α01, α02,......, α0p} ，可通過式(4)計算最優權值向量，其中多數樣本的Lagrange係數為零，因此

        即最優超平面的權向量是訓練樣本向量的線性組合，且只有支援向量影響最終的劃分結果，如果去掉其他訓練樣本重新訓練，得到分類超平面相同。但如果一個支援向量未能包含在訓練集內時，最優超平面會被改變。利用計算出的最優權值向量和一個正的支援向量，可)進一步計算出最優偏置

         求解線性可分問題得到的最優分類判別函式為

        在上式中的P個輸入向量中，只有若干個支援向量的Lagrange係數不為零，因此計算複雜度取決於支援向量的個數。對於線性可分資料，該判別函式對訓練樣本的分類誤差為零，而對非訓練樣本具有最佳泛化效能。