目標檢測的影象特徵提取之（二）LBP特徵

        LBP（Local Binary Pattern，區域性二值模式）是一種用來描述影象區域性紋理特徵的運算元；它具有旋轉不變性和灰度不變性等顯著的優點。它是首先由T. Ojala, M.Pietikäinen, 和D.Harwood 在1994年提出，用於紋理特徵提取。而且，提取的特徵是影象的區域性的紋理特徵；

1、LBP特徵的描述

原始的LBP運算元定義為在3*3的視窗內，以視窗中心畫素為閾值，將相鄰的8個畫素的灰度值與其進行比較，若周圍畫素值大於中心畫素值，則該畫素點的位置被標記為1，否則為0。這樣，3*3鄰域內的8個點經比較可產生

LBP的改進版本：

原始的LBP提出後，研究人員不斷對其提出了各種改進和優化。

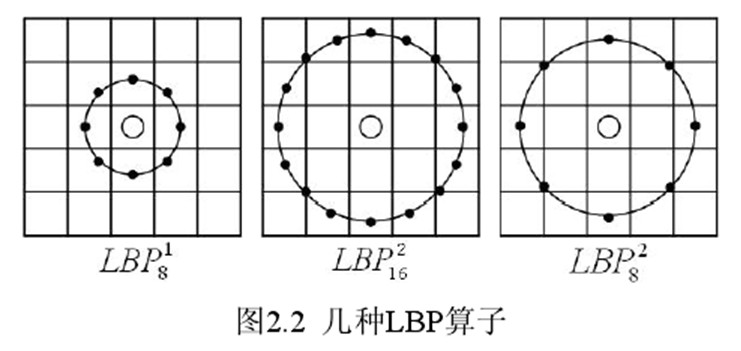
（1）圓形LBP運算元：

基本的LBP運算元的最大缺陷在於它只覆蓋了一個固定半徑範圍內的小區域，這顯然不能滿足不同尺寸和頻率紋理的需要。為了適應不同尺度的紋理特徵，並達到灰度和旋轉不變性的要求，Ojala等對LBP 運算元進行了改進，將3×3鄰域擴充套件到任意鄰域，並用圓形鄰域代替了正方形鄰域，改進後的LBP 運算元允許在半徑為R 的圓形鄰域內有任意多個畫素點。從而得到了諸如半徑為

（2）LBP旋轉不變模式

從LBP 的定義可以看出，LBP 運算元是灰度不變的，但卻不是旋轉不變的。影象的旋轉就會得到不同的LBP值。

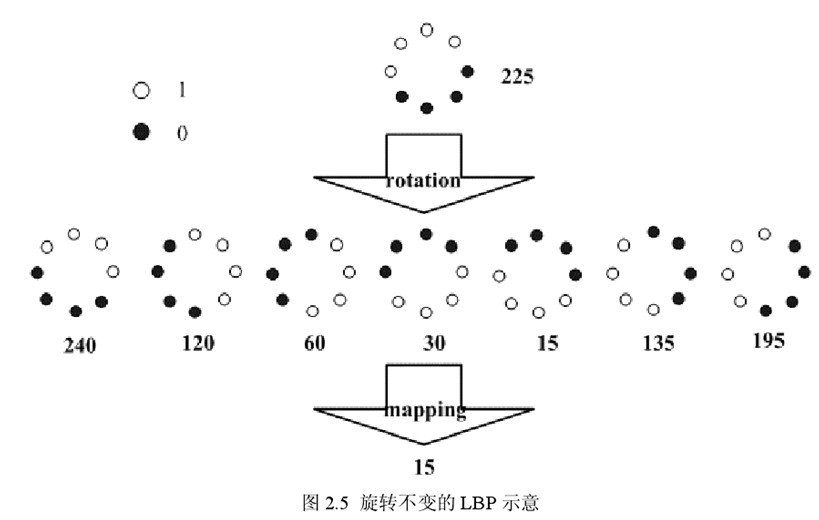
         Maenpaa等人又將LBP運算元進行了擴充套件，提出了具有旋轉不變性的LBP 運算元，即不斷旋轉圓形鄰域得到一系列初始定義的LBP值，取其最小值作為該鄰域的LBP 值。

圖2.5 給出了求取旋轉不變的LBP 的過程示意圖，圖中運算元下方的數字表示該運算元對應的LBP值，圖中所示的8 種LBP模式，經過旋轉不變的處理，最終得到的具有旋轉不變性的LBP值為15。也就是說，圖中的8種LBP 模式對應的旋轉不變的

（3）LBP等價模式

一個LBP運算元可以產生不同的二進位制模式，對於半徑為R的圓形區域內含有P個取樣點的LBP運算元將會產生P²種模式。很顯然，隨著鄰域集內取樣點數的增加，二進位制模式的種類是急劇增加的。例如：5×5鄰域內20個取樣點，有2²⁰＝1,048,576種二進位制模式。如此多的二值模式無論對於紋理的提取還是對於紋理的識別、分類及資訊的存取都是不利的。同時，過多的模式種類對於紋理的表達是不利的。例如，將LBP運算元用於紋理分類或人臉識別時，常採用LBP模式的統計直方圖來表達影象的資訊，而較多的模式種類將使得資料量過大，且直方圖過於稀疏。因此，需要對原始的LBP模式進行降維，使得資料量減少的情況下能最好的代表影象的資訊。

為了解決二進位制模式過多的問題，提高統計性，Ojala提出了採用一種“等價模式”（UniformPattern）來對LBP運算元的模式種類進行降維。Ojala等認為，在實際影象中，絕大多數LBP模式最多隻包含兩次從1到0或從0到1的跳變。因此，Ojala將“等價模式”定義為：當某個LBP所對應的迴圈二進位制數從0到1或從1到0最多有兩次跳變時，該LBP所對應的二進位制就稱為一個等價模式類。如00000000（0次跳變），00000111（只含一次從0到1的跳變），10001111（先由1跳到0，再由0跳到1，共兩次跳變）都是等價模式類。除等價模式類以外的模式都歸為另一類，稱為混合模式類，例如10010111（共四次跳變）（這是我的個人理解，不知道對不對）。

通過這樣的改進，二進位制模式的種類大大減少，而不會丟失任何資訊。模式數量由原來的2^P種減少為P ( P-1)+2種，其中P表示鄰域集內的取樣點數。對於3×3鄰域內8個取樣點來說，二進位制模式由原始的256種減少為58種，這使得特徵向量的維數更少，並且可以減少高頻噪聲帶來的影響。

2、LBP特徵用於檢測的原理

顯而易見的是，上述提取的LBP運算元在每個畫素點都可以得到一個LBP“編碼”，那麼，對一幅影象（記錄的是每個畫素點的灰度值）提取其原始的LBP運算元之後，得到的原始LBP特徵依然是“一幅圖片”（記錄的是每個畫素點的LBP值）。

        LBP的應用中，如紋理分類、人臉分析等，一般都不將LBP圖譜作為特徵向量用於分類識別，而是採用LBP特徵譜的統計直方圖作為特徵向量用於分類識別。

因為，從上面的分析我們可以看出，這個“特徵”跟位置資訊是緊密相關的。直接對兩幅圖片提取這種“特徵”，並進行判別分析的話，會因為“位置沒有對準”而產生很大的誤差。後來，研究人員發現，可以將一幅圖片劃分為若干的子區域，對每個子區域內的每個畫素點都提取LBP特徵，然後，在每個子區域內建立LBP特徵的統計直方圖。如此一來，每個子區域，就可以用一個統計直方圖來進行描述；整個圖片就由若干個統計直方圖組成；

例如：一幅100*100畫素大小的圖片，劃分為10*10=100個子區域（可以通過多種方式來劃分區域），每個子區域的大小為10*10畫素；在每個子區域內的每個畫素點，提取其LBP特徵，然後，建立統計直方圖；這樣，這幅圖片就有10*10個子區域，也就有了10*10個統計直方圖，利用這10*10個統計直方圖，就可以描述這幅圖片了。之後，我們利用各種相似性度量函式，就可以判斷兩幅影象之間的相似性了；

3、對LBP特徵向量進行提取的步驟

（1）首先將檢測視窗劃分為16×16的小區域（cell）；

（2）對於每個cell中的一個畫素，將相鄰的8個畫素的灰度值與其進行比較，若周圍畫素值大於中心畫素值，則該畫素點的位置被標記為1，否則為0。這樣，3*3鄰域內的8個點經比較可產生8位二進位制數，即得到該視窗中心畫素點的LBP值；

（3）然後計算每個cell的直方圖，即每個數字（假定是十進位制數LBP值）出現的頻率；然後對該直方圖進行歸一化處理。

（4）最後將得到的每個cell的統計直方圖進行連線成為一個特徵向量，也就是整幅圖的LBP紋理特徵向量；

然後便可利用SVM或者其他機器學習演算法進行分類了。

另外一篇部落格上的講解

#include "lbp.h"

#include <cv.h>

#include <highgui.h>

using namespacecv;

const doubleM_PI = 3.1415926;

//原始的LBP演算法實現

template <typename_Tp>

void lbp::OLBP_(constMat&src,Mat& dst) {

        dst = Mat::zeros(src.rows-2,src.cols-2,CV_8UC1);

        for(inti=1;i<src.rows-1;i++) {

                for(intj=1;j<src.cols-1;j++) {

                        _Tp center = src.at<_Tp>(i,j);

                        unsigned char code = 0;

                       code |= (src.at<_Tp>(i-1,j-1) > center)<< 7;

                       code |= (src.at<_Tp>(i-1,j) > center)<< 6;

                       code|= (src.at<_Tp>(i-1,j+1) > center)<< 5;

                       code|= (src.at<_Tp>(i,j+1) > center)<< 4;

                      code|= (src.at<_Tp>(i+1,j+1) > center)<< 3;

                        code |= (src.at<_Tp>(i+1,j) > center) << 2;

                       code|= (src.at<_Tp>(i+1,j-1) > center)<< 1;

                        code |= (src.at<_Tp>(i,j-1) > center) << 0;

                        dst.at<unsignedchar>(i-1,j-1) =code;

                }

        }

}

//LBP的改進版本

template <typename _Tp>

void lbp::ELBP_(constMat& src, Mat& dst,int radius,int neighbors) {

        neighbors = max(min(neighbors,31),1); // set bounds...

        // Note:alternatively you can switch to the new OpenCV Mat_

        // typesystem to define an unsigned int matrix... I am probably

        // mistakenhere, but I didn't see an unsigned int representation

        // inOpenCV's classic typesystem...

       dst = Mat::zeros(src.rows-2*radius, src.cols-2*radius, CV_32SC1);

        for(int n=0; n<neighbors; n++) {

                //sample points

                floatx = static_cast<float>(radius)* cos(2.0*M_PI*n/static_cast<float>(neighbors));

                floaty = static_cast<float>(radius)* -sin(2.0*M_PI*n/static_cast<float>(neighbors));

                //relative indices

                intfx = static_cast<int>(floor(x));

                intfy = static_cast<int>(floor(y));

                int cx = static_cast<int>(ceil(x));

                intcy = static_cast<int>(ceil(y));

                //fractional part

                floatty = y - fy;

                floattx = x - fx;

                //set interpolation weights

                float w1 =(1 - tx) * (1 - ty);

                floatw2 =      tx  * (1 - ty);

                floatw3 = (1 - tx) *      ty;

                floatw4 =      tx  *     ty;

                //iterate through your data

                for(int i=radius; i < src.rows-radius;i++) {

                        for(int j=radius;j <src.cols-radius;j++) {

                                float t = w1*src.at<_Tp>(i+fy,j+fx) +w2*src.at<_Tp>(i+fy,j+cx) + w3*src.at<_Tp>(i+cy,j+fx) +w4*src.at<_Tp>(i+cy,j+cx);

                                // we are dealing with floating point precision, so addsome little tolerance

                                              dst.at<float>(i-radius,j-radius)+= ((t > src.at<_Tp>(i,j)) && (abs(t-src.at<_Tp>(i,j))> std::numeric_limits<float>::epsilon()))<< n;

                               // dst.at<unsigned int>(i-radius,j-radius) += ((t >src.at<_Tp>(i,j)) && (abs(t-src.at<_Tp>(i,j)) >std::numeric_limits<float>::epsilon())) << n;

                        }

                }

        }

}

template <typename _Tp>

void lbp::VARLBP_(constMat& src, Mat& dst,int radius,int neighbors) {

        max(min(neighbors,31),1); // set bounds

        dst = Mat::zeros(src.rows-2*radius,src.cols-2*radius, CV_32FC1);//! result

        // allocatesome memory for temporary on-line variance calculations

        Mat _mean = Mat::zeros(src.rows,src.cols, CV_32FC1);

        Mat _delta = Mat::zeros(src.rows,src.cols, CV_32FC1);

        Mat _m2 = Mat::zeros(src.rows,src.cols, CV_32FC1);

        for(int n=0;n<neighbors; n++) {

                //sample points

                floatx = static_cast<float>(radius)* cos(2.0*M_PI*n/static_cast<float>(neighbors));

                floaty = static_cast<float>(radius)* -sin(2.0*M_PI*n/static_cast<float>(neighbors));

                //relative indices

                intfx = static_cast<int>(floor(x));

                intfy = static_cast<int>(floor(y));

                intcx = static_cast<int>(ceil(x));

                intcy = static_cast<int>(ceil(y));

                //fractional part

                floatty = y - fy;

                floattx = x - fx;

                //set interpolation weights

                floatw1 = (1 - tx) * (1 - ty);

                floatw2 =      tx  * (1 - ty);

                floatw3 = (1 - tx) *      ty;

                floatw4 =      tx  *     ty;

                //iterate through your data

                for(int i=radius; i < src.rows-radius;i++) {

                        for(int j=radius;j < src.cols-radius;j++){

                                float t = w1*src.at<_Tp>(i+fy,j+fx) +w2*src.at<_Tp>(i+fy,j+cx) + w3*src.at<_Tp>(i+cy,j+fx) +w4*src.at<_Tp>(i+cy,j+cx);

                                _delta.at<float>(i,j) = t - _mean.at<float>(i,j);

                                _mean.at<float>(i,j) = (_mean.at<float>(i,j) + (_delta.at<float>(i,j)/ (1.0*(n+1))));// i am a bit paranoid

                                _m2.at<float>(i,j) = _m2.at<float>(i,j)+ _delta.at<float>(i,j) * (t -_mean.at<float>(i,j));

                        }

                }

        }

        // calculateresult

        for(int i = radius; i < src.rows-radius; i++) {

                for(int j = radius; j < src.cols-radius; j++) {

                        dst.at<float>(i-radius, j-radius) = _m2.at<float>(i,j) / (1.0*(neighbors-1));

                }

        }

}