2. 程式人生 > >Decoupled Networks 論文筆記

Decoupled Networks 論文筆記

阿新 • • 發佈：2019-01-04

0 摘要

    基於內積運算的卷積操作一直是卷積神經網路（CNN）的核心元件，也是學習視覺表示的關鍵。我們觀察發現，CNN學習的特徵是類內差異（特徵的幅值）和類間差異（特徵間的夾角，語義差異）的耦合。我們提出了一種通用的解耦學習框架，該框架對類內差異和類間差異進行獨立的建模。具體而言，我們首先將內積重新分解為解耦的形式，然後將其推廣到解耦卷積運算元，利用該運算元構建解耦網路。我們提出瞭解耦卷積運算元的幾個例項。每個解耦運算元具有直觀的幾何解釋。基於這些解耦運算元，解耦網路直接從資料中學習。大量實驗表明，這種解耦具有比較顯著的效能，並且易於收斂，魯棒性更強。

1 介紹

    卷積神經網路推動了許多視覺任務的發展，包括物體識別，物體檢測，語義分割等。最近的研究中有相當一部分對CNN的結構進行改進（如ResNet的short cut和GoogLeNet的多分支卷積），他們著重於提高網路深度和表示能力。 儘管取得了這些進展，但理解卷積網路是如何產生有區分力的表示，並且能良好地泛化仍然是一個有趣的問題。
    目前的卷積操作：

f(w,x)=<w,x>=wTx，其本質上是一個矩陣相乘計算兩個矩陣的相似度操作。這個操作將類間差異和類內差異統一在一個度量中。因此，當兩個樣本之間的內積較大時，無法判斷這兩個樣本是類內差異造成的還是類間的差異造成的。（也就是說當你通過卷積操作得到的結果很相似的時候，你並不能夠得到一個結論說這兩個很相似，反之亦不能，因為你不能夠區別這種差異或者是相似度是類內差異造成的還是類間的差異造成的）。為了更好地研究CNN表示的屬性並進一步改進現有框架，我們建議明確區分類間差異和類內變異。具體來說，我們用幅值和角度來重新設計內積，比如：||w||2||x||2cos(θ(w,x))。
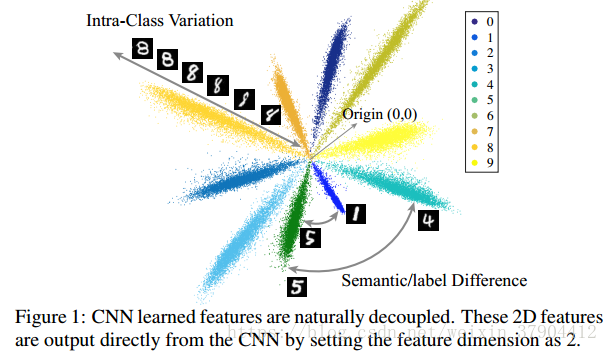
這裡寫圖片描述
圖1是CNN在手寫體識別任務上學到的特徵的2D視覺化示意圖。 0~9每一個手寫體數字對應的特徵是圖中的一束；任意一束當中的不同位置表示的是同一類別的不同表徵，也就是類間差距（intra-class Variations）；束與束之間形成的夾角表達的是兩個類別之間的差距（inter-class difference），也就是這裡所謂的語義差異。這種解耦現象促使我們提出解耦卷積運算元。我們希望內積中的解耦幅值和角度能更好地模擬深層網路中的類內差異和類間差異。
    我們通過將傳統的基於內積的卷積運算元推廣到解耦運算元，提出了一種新的解耦網路（DCNet）。（如果不解耦會存在一個什麼樣的問題呢？就是說你只能得到一個最終的結果，但是對於兩個同樣的輸出，你不能分辨造成這個結果的原因是因為他們實際就是同一種類別，還是因為剛好 ab =cd。）那麼具體怎麼解耦呢？ 作者給出的解決方案：
f(w,x)=||w||2||x||2cos(θ(w,x))=h(||w||,||x||)×g(θ(w,x))。
其中，θ=arccoswTx||wT||2||x||2
    將卷積操作解耦為幅值（Norm）和角度（Angle）兩部分，並且將這兩部分分別用兩個函式h(.) 和g(.)來表示。關於角度的函式g(.)則度量著類間差異（inter-class difference），關於幅值的函式h(.)則度量著類內差異（intra-class variations），同時其值的大小也就表示了這個類別的可信度。解耦卷積提供了一種更通用的框架以更好區分類間差異和類內差異，並且傳統的卷積操作就變成了解耦網路的一個特例：h(||w||,||x||)=||w||2||x||2,g(θ(w,x))=cos(θ(w,x))。
    從解耦的角度來看，原始的CNN基於一個強有力的假設，即類內變異可以通過正規化乘法來線性建模，而類間差異由角度餘弦來描述。 但是，這種建模方法不一定適用於所有任務。 通過解耦學習框架，我們可以根據不同的任務設計解耦運算子，也可以直接從資料中學習。 DCNets的優點有四個方面：
1.DCNets不僅允許我們使用一些替代函式來更好地模擬類內差異和類間差異，而且它們還使我們能夠直接學習這些函式，而不是擬合它們。
2.DCNets可以更快地收斂，同時達到與原始CNN相當甚至更好的精度。
3.DCNets的一些例項可以具有更強的魯棒性可以抵抗對抗樣本的攻擊。我們可以用有界的h(·)來壓縮每個類的特徵空間，這可以帶來魯棒性。
4.解耦的運算子非常靈活，並且與架構無關。 他們可以很容易地適應VGG，GoogLeNet，ResNet。
    具體而言，我們提出了兩種不同型別的解耦卷積運算元：有界運算元和無界運算元。 我們為每種型別的解耦運算元提供多個例項。 從經驗上講，有界運算元可能會產生更快的收斂速度和更好的抵抗對抗樣本攻擊的魯棒性，無界運算元可能具有更好的表徵能力。 這些解耦運算元可以是平滑的也可以是不平滑的，會產生不同的行為。 此外，我們引入了一個新的概念： 解耦運算元的運算元半徑operator radius。運算元半徑描述了幅值函式h(·)的導數相對於輸入||x||的變化。 通過反向傳播學習運算元半徑，我們進一步提出了可學習的解耦運算元。 此外，我們還展示了一些優化這些運算元的替代方法，這些運算元由標準的反向傳播學習。。我們的貢獻如下：
1.受CNN特徵解耦觀察的啟發，我們提出了一個解耦框架來研究神經網路。
2.傳統CNNs對類間差異和類內差異做了強有力的假設，這可能不是最優的。 通過解耦內積，我們能夠設計更有效的幅度和角度函式。
3.與標準CNN相比，DCNets更容易收斂，精度更高，魯棒性更強。

2 相關工作

    越來越多的工作側重於改善分類層（最後一個softmax層）以增加學習特徵的區分性。 相反，解耦學習提供了一個更加普遍和更加系統的方式來研究CNN。在我們的框架中，先前的工作（改善分類層）可以看成對最後的softmax層優化h(||w||,||x||) 和