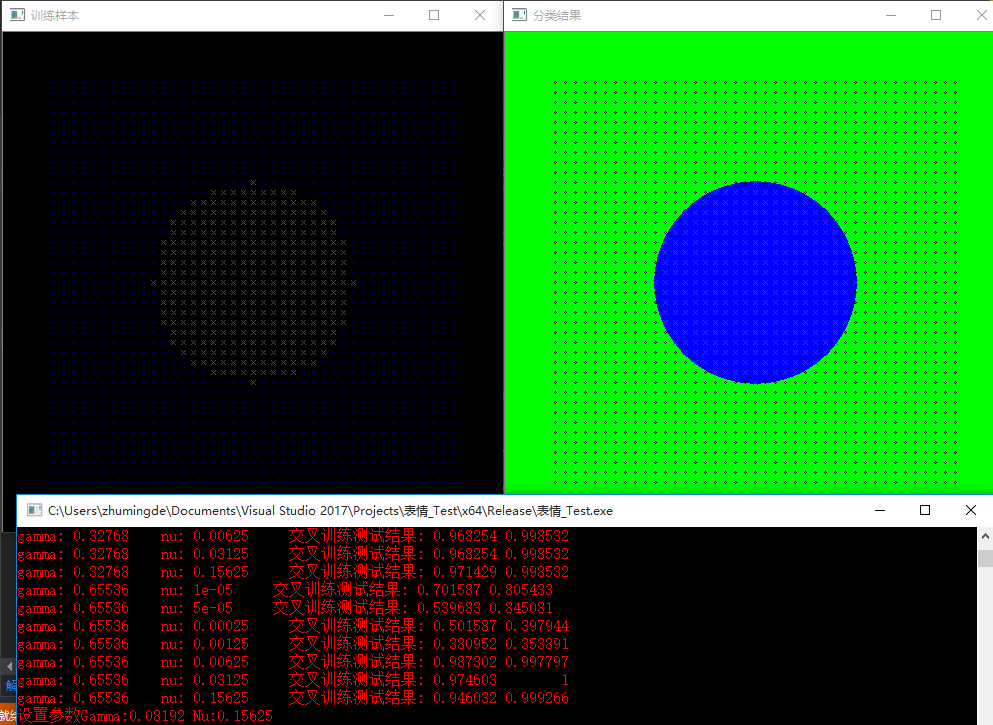
慣例先放結果圖，左側為訓練樣本，右側為訓練完後的分類演示圖

Dlib的支援向量機用起來比Opencv的爽多了，

支援交叉驗證，

降低支援向量的個數

以及兩種方式判別類別（正負以及可能性兩種）

然後就是簡單粗暴的程式碼了：

//需要配置Opencv以及Dlib的環境

Dlib配置見： 地址

Opencv配置見：地址

// The contents of this file are in the public domain. See LICENSE_FOR_EXAMPLE_PROGRAMS.txt
/*

This is an example illustrating the use of the support vector machine
utilities from the dlib C++ Library.

This example creates a simple set of data to train on and then shows
you how to use the cross validation and svm training functions
to find a good decision function that can classify examples in our
data set.


The data used in this example will be 2 dimensional data and will
come from a distribution where points with a distance less than 10
from the origin are labeled +1 and all other points are labeled
as -1.

*/


#include <iostream>
#include <dlib/svm.h>
#include<opencv2/opencv.hpp>
using namespace std;
using namespace dlib;
using namespace cv;

int main()
{

	// The svm functions use column vectors to contain a lot of the data on which they
	// operate. So the first thing we do here is declare a convenient typedef.  

	// This typedef declares a matrix with 2 rows and 1 column.  It will be the object that
	// contains each of our 2 dimensional samples.   (Note that if you wanted more than 2
	// features in this vector you can simply change the 2 to something else.  Or if you
	// don't know how many features you want until runtime then you can put a 0 here and
	// use the matrix.set_size() member function)
	typedef matrix<double, 2, 1> sample_type;

	// This is a typedef for the type of kernel we are going to use in this example.  In
	// this case I have selected the radial basis kernel that can operate on our 2D
	// sample_type objects
	typedef radial_basis_kernel<sample_type> kernel_type;


	// Now we make objects to contain our samples and their respective labels.
	std::vector<sample_type> samples;
	std::vector<double> labels;

	int 寬 = 500, 高 = 500;
	Mat 演示圖片 = Mat::zeros(高, 寬, CV_8UC3);

	for (int r = -20; r <= 20; ++r)
	{
		for (int c = -20; c <= 20; ++c)
		{
			// if this point is less than 10 from the origin
			if (sqrt((double)r*r + c*c) <= 10)
			{
				line(演示圖片, Point(c * 10 + 250 - 2, r * 10 + 250 - 2), Point(c * 10 + 250 + 2, r * 10 + 250 + 2), Scalar(0, 0, 255));
				line(演示圖片, Point(c * 10 + 250 - 2, r * 10 + 250 + 2), Point(c * 10 + 250 + 2, r * 10 + 250 - 2), Scalar(0, 0, 255));
			}
			else
				circle(演示圖片, Point(c * 10 + 250, r * 10 + 250), 1, Scalar(100));

		}
	}

	imshow("訓練樣本", 演示圖片);
	waitKey(1);

	// Now let's put some data into our samples and labels objects.  We do this by looping
	// over a bunch of points and labeling them according to their distance from the
	// origin.
	for (int r = -20; r <= 20; ++r)
	{
		for (int c = -20; c <= 20; ++c)
		{
			sample_type samp;
			samp(0) = r;
			samp(1) = c;
			samples.push_back(samp);

			// if this point is less than 10 from the origin
			if (sqrt((double)r*r + c*c) <= 10)
				labels.push_back(+1);
			else
				labels.push_back(-1);

		}
	}


	// Here we normalize all the samples by subtracting their mean and dividing by their
	// standard deviation.  This is generally a good idea since it often heads off
	// numerical stability problems and also prevents one large feature from smothering
	// others.  Doing this doesn't matter much in this example so I'm just doing this here
	// so you can see an easy way to accomplish this with the library.  
	vector_normalizer<sample_type> normalizer;
	// let the normalizer learn the mean and standard deviation of the samples
	normalizer.train(samples);
	// now normalize each sample
	for (unsigned long i = 0; i < samples.size(); ++i)
		samples[i] = normalizer(samples[i]);


	// Now that we have some data we want to train on it.  However, there are two
	// parameters to the training.  These are the nu and gamma parameters.  Our choice for
	// these parameters will influence how good the resulting decision function is.  To
	// test how good a particular choice of these parameters is we can use the
	// cross_validate_trainer() function to perform n-fold cross validation on our training
	// data.  However, there is a problem with the way we have sampled our distribution
	// above.  The problem is that there is a definite ordering to the samples.  That is,
	// the first half of the samples look like they are from a different distribution than
	// the second half.  This would screw up the cross validation process but we can fix it
	// by randomizing the order of the samples with the following function call.
	randomize_samples(samples, labels);


	// The nu parameter has a maximum value that is dependent on the ratio of the +1 to -1
	// labels in the training data.  This function finds that value.
	const double max_nu = maximum_nu(labels);

	// here we make an instance of the svm_nu_trainer object that uses our kernel type.
	svm_nu_trainer<kernel_type> trainer;

	// Now we loop over some different nu and gamma values to see how good they are.  Note
	// that this is a very simple way to try out a few possible parameter choices.  You
	// should look at the model_selection_ex.cpp program for examples of more sophisticated
	// strategies for determining good parameter choices.
	cout << "開始測試各引數效果" << endl;
	double Gamma=0.00001, Nu=0.00001;
	double OK = 0;
	for (double gamma = 0.00001; gamma <= 1; gamma *= 2)
	{
		for (double nu = 0.00001; nu < max_nu; nu *= 5)
		{
			// tell the trainer the parameters we want to use
			trainer.set_kernel(kernel_type(gamma));
			trainer.set_nu(nu);

			cout << "gamma: " << gamma << "    nu: " << nu;
			// Print out the cross validation accuracy for 3-fold cross validation using
			// the current gamma and nu.  cross_validate_trainer() returns a row vector.
			// The first element of the vector is the fraction of +1 training examples
			// correctly classified and the second number is the fraction of -1 training
			// examples correctly classified.
			matrix<double>temp= cross_validate_trainer(trainer, samples, labels, 3);
			if (OK < (temp(0, 1) + temp(0, 0))) {
				OK = temp(0, 1) + temp(0, 0);
				Gamma = gamma;
				Nu = nu;
			}
			cout << "     交叉訓練測試結果: " << cross_validate_trainer(trainer, samples, labels, 3) ;
		}
	}
	

	// From looking at the output of the above loop it turns out that a good value for nu
	// and gamma for this problem is 0.15625 for both.  So that is what we will use.

	// Now we train on the full set of data and obtain the resulting decision function.  We
	// use the value of 0.15625 for nu and gamma.  The decision function will return values
	// >= 0 for samples it predicts are in the +1 class and numbers < 0 for samples it
	// predicts to be in the -1 class.
	//trainer.set_kernel(kernel_type(0.15625));
	//trainer.set_nu(0.15625);

	trainer.set_kernel(kernel_type(Gamma));
	trainer.set_nu(Nu);

	cout << "設定引數Gamma:" << Gamma << " Nu:" << Nu << endl;

	typedef decision_function<kernel_type> dec_funct_type;
	typedef normalized_function<dec_funct_type> funct_type;

	// Here we are making an instance of the normalized_function object.  This object
	// provides a convenient way to store the vector normalization information along with
	// the decision function we are going to learn.  
	funct_type learned_function;
	learned_function.normalizer = normalizer;  // save normalization information
	learned_function.function = trainer.train(samples, labels); // perform the actual SVM training and save the results



																// print out the number of support vectors in the resulting decision function
	cout << "\nnumber of support vectors in our learned_function is "
		<< learned_function.function.basis_vectors.size() << endl;

	// Now let's try this decision_function on some samples we haven't seen before.
	sample_type sample;

	sample(0) = 3.123;
	sample(1) = 2;
	cout << "This is a +1 class example, the classifier output is " << learned_function(sample) << endl;

	sample(0) = 3.123;
	sample(1) = 9.3545;
	cout << "This is a +1 class example, the classifier output is " << learned_function(sample) << endl;

	sample(0) = 13.123;
	sample(1) = 9.3545;
	cout << "This is a -1 class example, the classifier output is " << learned_function(sample) << endl;

	sample(0) = 13.123;
	sample(1) = 0;
	cout << "This is a -1 class example, the classifier output is " << learned_function(sample) << endl;


	// We can also train a decision function that reports a well conditioned probability
	// instead of just a number > 0 for the +1 class and < 0 for the -1 class.  An example
	// of doing that follows:
	typedef probabilistic_decision_function<kernel_type> probabilistic_funct_type;
	typedef normalized_function<probabilistic_funct_type> pfunct_type;

	pfunct_type learned_pfunct;
	learned_pfunct.normalizer = normalizer;
	learned_pfunct.function = train_probabilistic_decision_function(trainer, samples, labels, 3);
	// Now we have a function that returns the probability that a given sample is of the +1 class.  

	// print out the number of support vectors in the resulting decision function.  
	// (it should be the same as in the one above)
	cout << "\nnumber of support vectors in our learned_pfunct is "
		<< learned_pfunct.function.decision_funct.basis_vectors.size() << endl;

	sample(0) = 3.123;
	sample(1) = 2;
	cout << "This +1 class example should have high probability.  Its probability is: "
		<< learned_pfunct(sample) << endl;

	sample(0) = 3.123;
	sample(1) = 9.3545;
	cout << "This +1 class example should have high probability.  Its probability is: "
		<< learned_pfunct(sample) << endl;

	sample(0) = 13.123;
	sample(1) = 9.3545;
	cout << "This -1 class example should have low probability.  Its probability is: "
		<< learned_pfunct(sample) << endl;

	sample(0) = 13.123;
	sample(1) = 0;
	cout << "This -1 class example should have low probability.  Its probability is: "
		<< learned_pfunct(sample) << endl;



	// Another thing that is worth knowing is that just about everything in dlib is
	// serializable.  So for example, you can save the learned_pfunct object to disk and
	// recall it later like so:
	serialize("saved_function.dat") << learned_pfunct;

	// Now let's open that file back up and load the function object it contains.
	deserialize("saved_function.dat") >> learned_pfunct;

	// Note that there is also an example program that comes with dlib called the
	// file_to_code_ex.cpp example.  It is a simple program that takes a file and outputs a
	// piece of C++ code that is able to fully reproduce the file's contents in the form of
	// a std::string object.  So you can use that along with the std::istringstream to save
	// learned decision functions inside your actual C++ code files if you want.  




	// Lastly, note that the decision functions we trained above involved well over 200
	// basis vectors.  Support vector machines in general tend to find decision functions
	// that involve a lot of basis vectors.  This is significant because the more basis
	// vectors in a decision function, the longer it takes to classify new examples.  So
	// dlib provides the ability to find an approximation to the normal output of a trainer
	// using fewer basis vectors.  

	// Here we determine the cross validation accuracy when we approximate the output using
	// only 10 basis vectors.  To do this we use the reduced2() function.  It takes a
	// trainer object and the number of basis vectors to use and returns a new trainer
	// object that applies the necessary post processing during the creation of decision
	// function objects.
	cout << "\ncross validation accuracy with only 10 support vectors: "
		<< cross_validate_trainer(reduced2(trainer, 10), samples, labels, 3);

	// Let's print out the original cross validation score too for comparison.
	cout << "cross validation accuracy with all the original support vectors: "
		<< cross_validate_trainer(trainer, samples, labels, 3);

	// When you run this program you should see that, for this problem, you can reduce the
	// number of basis vectors down to 10 without hurting the cross validation accuracy. 


	// To get the reduced decision function out we would just do this:
	learned_function.function = reduced2(trainer, 10).train(samples, labels);
	// And similarly for the probabilistic_decision_function: 
	learned_pfunct.function = train_probabilistic_decision_function(reduced2(trainer, 10), samples, labels, 3);
	cout << "\nnumber of support vectors in our learned_function is "
		<< learned_function.function.basis_vectors.size() << endl;

	Vec3b green(0, 255, 0), blue(255, 0, 0), red(0, 0, 255), black(0, 0, 0);
	for (int i = 0; i < 演示圖片.rows; ++i)
		for (int j = 0; j < 演示圖片.cols; ++j)
		{
			Mat sampleMat = (Mat_<float>(1, 2) << j, i);
			sample_type sample;

			sample(0) = (i - 250) / 10.0;
			sample(1) = (j - 250) / 10.0;
			float response = learned_function(sample);


			if (response <0)
				演示圖片.at<Vec3b>(i, j) = green;
			else if (response >= 0)
				演示圖片.at<Vec3b>(i, j) = blue;
			else if (response == 3)
				演示圖片.at<Vec3b>(i, j) = red;
			else if (response == 4)
				演示圖片.at<Vec3b>(i, j) = black;
		}

	for (int r = -20; r <= 20; ++r)
	{
		for (int c = -20; c <= 20; ++c)
		{
			// if this point is less than 10 from the origin
			if (sqrt((double)r*r + c*c) <= 10)
			{
				line(演示圖片, Point(c * 10 + 250-2, r * 10 + 250-2), Point(c * 10 + 250+2, r * 10 + 250+2), Scalar(0, 0, 255));
				line(演示圖片, Point(c * 10 + 250-2, r * 10 + 250+2), Point(c * 10 + 250+2, r * 10 + 250-2), Scalar(0, 0, 255));
			}
			else
				circle(演示圖片, Point(c * 10 + 250, r * 10 + 250), 1, Scalar(0));

		}
	}

	imshow("分類結果", 演示圖片);
	waitKey(-1);
	system("pause");
}