1. 蒙特卡羅方法的基本思想

蒙特卡羅方法又叫統計模擬方法，它使用隨機數（或偽隨機數）來解決計算的問題，是一類重要的數值計算方法。該方法的名字來源於世界著名的賭城蒙特卡羅，而蒙特卡羅方法正是以概率為基礎的方法。

一個簡單的例子可以解釋蒙特卡羅方法，假設我們需要計算一個不規則圖形的面積，那麼圖形的不規則程度和分析性計算（比如積分）的複雜程度是成正比的。而採用蒙特卡羅方法是怎麼計算的呢？首先你把圖形放到一個已知面積的方框內，然後假想你有一些豆子，把豆子均勻地朝這個方框內撒，散好後數這個圖形之中有多少顆豆子，再根據圖形內外豆子的比例來計算面積。當你的豆子越小，撒的越多的時候，結果就越精確。

2. 增強學習中的蒙特卡羅方法

現在我們開始講解增強學習中的蒙特卡羅方法，與上篇的DP不同的是，這裡不需要對環境的完整知識。蒙特卡羅方法僅僅需要經驗就可以求解最優策略，這些經驗可以線上獲得或者根據某種模擬機制獲得。

要注意的是，我們僅將蒙特卡羅方法定義在episode task上，所謂的episode task就是指不管採取哪種策略π，都會在有限時間內到達終止狀態並獲得回報的任務。比如玩棋類遊戲，在有限步數以後總能達到輸贏或者平局的結果並獲得相應回報。

那麼什麼是經驗呢？經驗其實就是訓練樣本。比如在初始狀態s，遵循策略π，最終獲得了總回報R，這就是一個樣本。如果我們有許多這樣的樣本，就可以估計在狀態s下，遵循策略π的期望回報，也就是狀態值函式Vπ(s)了。蒙特卡羅方法就是依靠樣本的平均回報來解決增強學習問題的。

儘管蒙特卡羅方法和動態規劃方法存在諸多不同，但是蒙特卡羅方法借鑑了很多動態規劃中的思想。在動態規劃中我們首先進行策略估計，計算特定策略π對應的Vπ和Qπ，然後進行策略改進，最終形成策略迭代。這些想法同樣在蒙特卡羅方法中應用。

3. 蒙特卡羅策略估計(Monte Carlo Policy evalution)

首先考慮用蒙特卡羅方法來學習狀態值函式Vπ(s)。如上所述，估計Vπ(s)的一個明顯的方法是對於所有到達過該狀態的回報取平均值。這裡又分為first-visit MC methods和every-visit MC methods。這裡，我們只考慮first MC methods，即在一個episode內，我們只記錄s的第一次訪問，並對它取平均回報。

現在我們假設有如下一些樣本，取折扣因子γ=1，即直接計算累積回報，則有

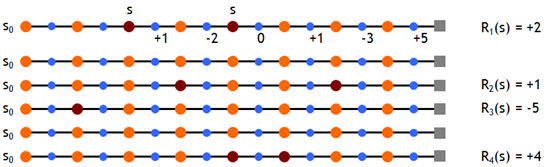
根據first MC methods，對出現過狀態s的episode的累積回報取均值，有Vπ(s)≈ (2 + 1 – 5 + 4)/4 = 0.5

    容易知道，當我們經過無窮多的episode後，Vπ(s)的估計值將收斂於其真實值。

4. 動作值函式的MC估計(Mote Carlo Estimation of Action Values)

在狀態轉移概率p(s'|a,s)已知的情況下，策略估計後有了新的值函式，我們就可以進行策略改進了，只需要看哪個動作能獲得最大的期望累積回報就可以。然而在沒有準確的狀態轉移概率的情況下這是不可行的。為此，我們需要估計動作值函式Qπ(s,a)。Qπ(s,a)的估計方法前面類似，即在狀態s下采用動作a，後續遵循策略π獲得的期望累積回報即為Qπ(s,a)，依然用平均回報來估計它。有了Q值，就可以進行策略改進了

5. 持續探索(Maintaining Exploration)

下面我們來探討一下Maintaining Exploration的問題。前面我們講到，我們通過一些樣本來估計Q和V，並且在未來執行估值最大的動作。這裡就存在一個問題，假設在某個確定狀態s0下，能執行a0, a1, a2這三個動作，如果智慧體已經估計了兩個Q函式值，如Q(s0,a0), Q(s0,a1)，且Q(s0,a0)>Q(s0,a1)，那麼它在未來將只會執行一個確定的動作a0。這樣我們就無法更新Q(s0,a1)的估值和獲得Q(s0,a2)的估值了。這樣的後果是，我們無法保證Q(s0,a0)就是s0下最大的Q函式。

Maintaining Exploration的思想很簡單，就是用soft policies來替換確定性策略，使所有的動作都有可能被執行。比如其中的一種方法是ε-greedy policy，即在所有的狀態下，用1-ε的概率來執行當前的最優動作a0，ε的概率來執行其他動作a1, a2。這樣我們就可以獲得所有動作的估計值，然後通過慢慢減少ε值，最終使演算法收斂，並得到最優策略。簡單起見，在下面MC控制中，我們使用exploring start，即僅在第一步令所有的a都有一個非零的概率被選中。

6. 蒙特卡羅控制(Mote Carlo Control)

我們看下MC版本的策略迭代過程：

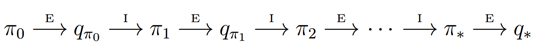
根據前面的說法，值函式Qπ(s,a)的估計值需要在無窮多episode後才能收斂到其真實值。這樣的話策略迭代必然是低效的。在上一篇DP中，我們了值迭代演算法，即每次都不用完整的策略估計，而僅僅使用值函式的近似值進行迭代，這裡也用到了類似的思想。每次策略的近似值，然後用這個近似值來更新得到一個近似的策略，並最終收斂到最優策略。這個思想稱為廣義策略迭代。

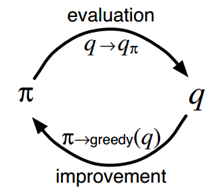
具體到MC control，就是在每個episode後都重新估計下動作值函式（儘管不是真實值），然後根據近似的動作值函式，進行策略更新。這是一個episode by episode的過程。

一個採用exploring starts的Monte Carlo control演算法，如下圖所示，稱為Monte Carlo ES。而對於所有狀態都採用soft policy的版本，這裡不再討論。

7. 小結

Monte Carlo方法的一個顯而易見的好處就是我們不需要環境模型了，可以從經驗中直接學到策略。它的另一個好處是，它對所有狀態s的估計都是獨立的，而不依賴與其他狀態的值函式。在很多時候，我們不需要對所有狀態值進行估計，這種情況下蒙特卡羅方法就十分適用。

不過，現在增強學習中，直接使用MC方法的情況比較少，而較多的採用TD演算法族。但是如同DP一樣，MC方法也是增強學習的基礎之一，因此依然有學習的必要。