一、什麼是不精確一維搜尋方法

一維搜尋方法是 求函式的最小值，來得到最優步長，不精確一維搜尋方法，即保證目標函式在每次迭代有滿意的下降量的方法。到一次滿意的水平，就是可接受步長。

二、幾個不精確一維搜尋方法的準則  引用地址

line search（一維搜尋，或線搜尋）是最優化（Optimization）演算法中的一個基礎步驟/演算法。它可以分為精確的一維搜尋以及不精確的一維搜尋兩大類。 在本文中，我想用“人話”解釋一下不精確的一維搜尋的兩大準則：Armijo-Goldstein準則 ＆ Wolfe-Powell準則。 之所以這樣說，是因為我讀到的所有最優化的書或資料，從來沒有一個可以用初學者都能理解的方式來解釋這兩個準則，它們要麼是長篇大論、把一堆數學公式丟給你去琢磨；要麼是簡短省略、直接略過了解釋的步驟就一句話跨越千山萬水得出了結論。 每當看到這些書的時候，我腦子裡就一個反應：你們就不能寫人話嗎？ 我下面就嘗試用通俗的語言來描述一下這兩個準則。

【1】為什麼要遵循這些準則

由於採用了不精確的一維搜尋，所以，為了能讓演算法收斂（即：求得極小值），人們逐漸發現、證明了一些規律，當你遵循這些規律的時候，演算法就很有可能收斂。因此，為了達到讓演算法收斂的目的，我們就要遵循這些準則。如果你不願意遵循這些已經公認有效的準則，而是要按自己的準則來設計演算法，那麼恭喜你，如果你能證明你的做法是有效的，未來若干年後，書本里可能也會出現你的名字。

【2】Armijo-Goldstein準則

此準則是在196X年的時候由Armijo和Goldstein提出的，當然我沒有具體去搜過這倆人是誰。在有的資料裡，你可能會看到“Armijo rule”（Armijo準則）的說法，可能是同一回事，不過，任何一個對此作出重要貢獻的人都是不可抹殺的，不是麼？

Armijo-Goldstein準則的核心思想有兩個：①目標函式值應該有足夠的下降；②一維搜尋的步長α不應該太小。

這兩個思想的意圖非常明顯。由於最優化問題的目的就是尋找極小值，因此，讓目標函式函式值“下降”是我們努力的方向，所以①正是想要保證這一點。

同理，②也類似：如果一維搜尋的步長α太小了，那麼我們的搜尋類似於在原地打轉，可能也是在浪費時間和精力。

文章來源：http://www.codelast.com/ 有了這兩個指導思想，我們來看看Armijo-Goldstein準則的數學表示式：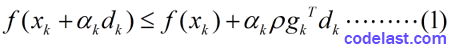

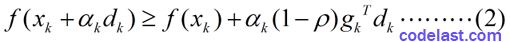
其中， 0<ρ<12  (1)為什麼要規定 ρ∈(0,12) 這個條件？其實可以證明：如果沒有這個條件的話，將影響演算法的超線性收斂性（

定義看這個連結，第4條）。在這個速度至關重要的時代，沒有超線性收斂怎麼活啊！(開個玩笑) 具體的證明過程，大家可以參考袁亞湘寫的《最優化理論與方法》一書，我沒有仔細看，我覺得對初學者，不用去管它。 (2)第1個不等式的左邊式子的泰勒展開式為： f(xk+αkdk)=f(xk)+αkgkTdk+o(αk)  去掉高階無窮小，剩下的部分為： f(xk)+αkgkTdk  而第一個不等式右邊與之只差一個係數 ρ  我們已知了 gkTdk<0 （這是 dk 為下降方向的充要條件），並且 ρ∈(0,12) ，因此，1式右邊仍然是一個比 f(xk) 小的數，即： f(xk)+αkρgkTdk<f(xk)  也就是說函式值是下降的（下降是最優化的目標）。 (3)由於 ρ∈(0,12) 且 gkTdk<0 （ dk 是一個下降方向的充要條件），故第2個式子右邊比第1個式子右邊要小，即： αk(1−ρ)gkTdk<αkρgkTdk<0  如果步長 α 太小的話，會導致這個不等式接近於不成立的邊緣。因此，式2就保證了 α 不能太小。 (4)我還要把很多書中都用來描述Armijo-Goldstein準則的一幅圖搬出來說明一下（親自手繪）：

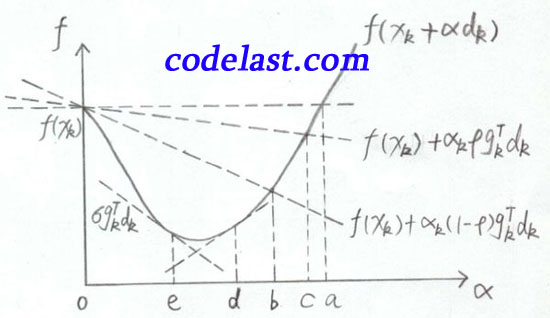
橫座標是 α ，縱座標是 f ，表示在 xk,dk 均為常量、 α 為自變數變化的情況下，目標函式值隨之變化的情況。 之所以說 xk,dk 均為常量，是因為在一維搜尋中，在某一個確定的點 xk 上，搜尋方向 dk 確定後，我們只需要找到一個合適的步長 α 就可以了。 當 x 為常量， α 為自變數時， f(x+αd) 可能是非線性函式（例如目標函式為 y=x2 時）。因此圖中是一條曲線。 右上角的 f(xk+αdk) 並不是表示一個特定點的值，而是表示這條曲線是以 α 為自變數、 xk,dk 為常量的函式圖形。 當 α=0 時，函式值為 f(xk) ，如圖中左上方所示。水平的那條虛線是函式值為 f(xk) 的基線，用於與其他函式值對比。 f(xk)+αkρgkTdk 那條線在 f(xk) 下方（前面已經分析過了，因為 gkTdk<0 ）， f(xk)+αk(1−ρ)gkTdk 又在 f(xk)+αkρgkTdk 的下方（前面也已經分析過了），所以Armijo-Goldstein準則可能會把極小值點（可接受的區間）判斷在區間bc內。顯而易見，區間bc是有可能把極小值排除在外的（極小值在區間ed內）。 所以，為了解決這個問題，Wolfe-Powell準則應運而生。 【3】Wolfe-Powell準則 在某些書中，你會看到“Wolfe conditions”的說法，應該和Wolfe-Powell準則是一回事——可憐的Powell大神又被無情地忽略了... Wolfe-Powell準則也有兩個數學表示式，其中，第一個表示式與Armijo-Goldstein準則的第1個式子相同，第二個表示式為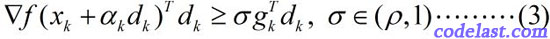： 這個式子已經不是關於函式值的了，而是關於梯度的。 此式的幾何解釋為：可接受點處的切線斜率≥初始斜率的 σ 倍。 上面的圖已經標出了 σgTkdk 那條線（即 e 點處的切線），而初始點（ α=0 的點）處的切線是比 e 點處的切線要“斜”的，由於 σ∈(ρ,1) ，使得 e 點處的切線變得“不那麼斜”了——不知道這種極為通俗而不夠嚴謹的說法，是否有助於你理解。 這樣做的結果就是，我們將極小值包含在了可接受的區間內（ e 點右邊的區間）。 Wolfe-Powell準則到這裡還沒有結束！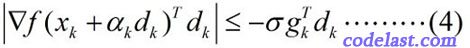在某些書中，你會看到用另一個所謂的“更強的條件”來代替(3)式，即： 這個式子和(3)式相比，就是左邊加了一個絕對值符號，右邊換了一下正負號（因為 gTkdk<0 ，所以 −σgTkdk>0 ）。 這樣做的結果就是：可接受的區間被限制在了 [b,d] 內，如圖：

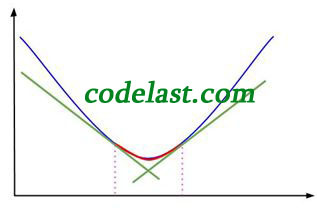
圖中紅線即為極小值被“夾擊”的生動演示。