單調棧

性質

單調棧是一種特殊的棧，特殊之處在於棧內的元素都保持一個單調性，可能為單調遞增，也可能為單調遞減。

模型

例如下圖就是一個單調遞增的單調棧。

其中的元素從小到大排列。

那麼，如果我們要加入一個新的元素5，5>4，符合要求，就可以直接加入。

那麼如果我們需要加入一個元素3呢？
為了維護單調棧的單調性，我們需要把從棧頂開始，大於3的元素全部彈出，再加入元素3。

如圖，我們彈出了4,5。

然後再加入3。
這就是單調棧的基本操作。
那麼單調棧能幹什麼呢，我們通過一道例題來了解。

Largest Rectangle in a Histogram

題目描述

A histogram is a polygon composed of a sequence of rectangles aligned at a common base line. The rectangles have equal widths but may have different heights. For example, the figure on the left shows the histogram that consists of rectangles with the heights 2, 1, 4, 5, 1, 3, 3, measured in units where 1 is the width of the rectangles:

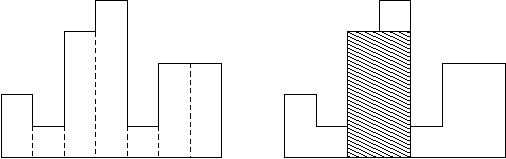
Usually, histograms are used to represent discrete distributions, e.g., the frequencies of characters in texts. Note that the order of the rectangles, i.e., their heights, is important. Calculate the area of the largest rectangle in a histogram that is aligned at the common base line, too. The figure on the right shows the largest aligned rectangle for the depicted histogram.

這道題讓求直方圖中最大的矩形
輸入和輸出

Input

The input contains several test cases. Each test case describes a histogram and starts with an integer n, denoting the number of rectangles it is composed of. You may assume that 1<=n<=100000. Then follow n integers h1,…,hn, where 0<=hi<=1000000000. These numbers denote the heights of the rectangles of the histogram in left-to-right order. The width of each rectangle is 1. A zero follows the input for the last test case.

輸入包含多組資料。每組資料包含一行，第一個正整數N表示有N個矩形，接下來N個正整數描述其高度。 資料以N=0結束。 資料範圍參看英文題面。

Output

For each test case output on a single line the area of the largest rectangle in the specified histogram. Remember that this rectangle must be aligned at the common base line.

對於每組資料輸出一行包含一個正整數，表示該組資料的答案。
樣例

Sample Input

7 2 1 4 5 1 3 3
4 1000 1000 1000 1000
0

Sample Output

8
4000

資料規模與約定

時間限制：1s1s

空間限制：64MB

解析

這其實是一道單調棧模板題。先思考一個問題，如果題目中的矩形的高度都是單調遞增的，如何得到最優解？顯然有一個貪心的策略，就是以每一個矩形的高度作為最終大矩形的高度，看最寬能是多少，然後統計最優解。
但如果進來的下一矩形比上一個低，它其實相當於限制了之前矩形的高度，那麼之前矩形比這個矩形高出的高度在以後的統計中就沒有絲毫用處了，如果我們在這個時候把以之前矩形的高度作為最終高度的答案統計掉，那麼反正以後的統計和上一個矩形沒有關係，還不如把他刪除。
這樣，我們實際上就得到了單調棧的模型，只需要維護一個單調棧，在維護單調性的彈出操作時統計寬度，更新答案即可在$O(n)$實際內得到最優解。
為了方便把最後剩下的，以及單調遞增的矩形也統計進去，我們假設a[n+1]的位置有一個高度為0的矩形，最後將它加入單調棧時他會將所有矩形都彈出，那麼答案也就完成最後的更新了。

#include<bits/stdc++.h>
using namespace std;
int n,height[100080]={},width[100080]={},Stack[100080]={},top=0;
inline bool input()
{
	scanf("%d",&n);
	if(!n)return false;
	for(int i=1;i<=n;i++)scanf("%d",&height[i]);
	height[n+1]=0;
	return true;
}
inline long long work()
{
	long long ans=0;
	for(int i=1;i<=n+1;i++)
	{
		if(height[i]>Stack[top])
		{
			Stack[++top]=height[i];width[top]=1;
		}
		else
		{
			int Widthsum=0;
			while(Stack[top]>height[i])
			{
				Widthsum+=width[top];
				ans=max(ans,(long long)Widthsum*Stack[top]);
				top--;
			}
			Stack[++top]=height[i];width[top]=Widthsum+1;
		}
	}	
	return ans;
}
int main()
{
	freopen("test.in","r",stdin);
	freopen("test.out","w",stdout);
	while(input())
	{
		printf("%lld\n",work());
		top=0;
		memset(Stack,0,sizeof(Stack));
		memset(height,0,sizeof(height));
		memset(width,0,sizeof(width));
	}
	return 0;
}

單調佇列

性質

單調佇列和單調棧很像，就是一個維護了單調性的佇列資料結構，可以是單調遞增的，也可以是單調遞減的。

模型

下圖是一個單調遞增的單調佇列模型。

其中元素也是從小到大排列。
和單調棧的操作一樣，如果加入一個滿足單調性的元素，例如5，那麼就直接加入。

那麼如果加入一個元素3呢？我們維護單調性，需要把佇列尾端把大於3的元素全部彈出，那麼就需要用雙端佇列來實現了，當然操作和單調棧是一樣的。

當然，佇列的基本操作是可以用的。例如，元素1,2出隊。

當然，一道例題。

最大子序和

Description

輸入一個長度為n的整數序列，從中找出一段不超過M的連續子序列，使得整個序列的和最大。

例如 1，-3,5,1，-2,3

當m=4時，S=5+1-2+3=7

當m=2或m=3時，S=5+1=6
Input Format

第一行兩個數n,m

第二行有n個數，要求在n個數找到最大子序和
Output Format

一個數，數出他們的最大子序和
Sample Input

6 4
1 -3 5 1 -2 3

Sample Output

7

Hint

資料範圍：

100%滿足n,m<=300000
Limitation

各個測試點1s

解析

首先，直接找區間最大和會比較困難，我們可以嘗試轉換問題模型。其實，求區間和問題就相當於找字首和的最大差值，在這道問題中，原問題就可以轉換為找到兩個位置x，y，使得sum[y]-sum[x]最大並且y-x≤m。
我們一重迴圈列舉右端點x，那麼問題就轉化為：找到左端點j，j∈[i-m,i-1]且j最小。
這就是我們單調佇列維護的物件。試考慮兩個位置j，k，如果j，k都滿足要求，且k>j,s[k]<s[j]，k就一定比j更優。因為它更接近i，即使j被剔除，k仍不一定被剔除，況且，s[k]<s[j]，它的數值也比j優，所以，無論從哪方面考慮，k都優於j，那麼等到k進入[i-m,i-1]的區間後，j就毫無用處了，我們可以刪除j。這些操作就維護了一個單調佇列，而單調佇列就保證了對頭的元素最優。我們就可以O(n)的求解這個問題了。

#include<bits/stdc++.h>
using namespace std;
int n,m,num[300080]={},s[300080]={};
deque< int >Q;
inline void input()
{
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++)
	{
		scanf("%d",&num[i]);
		s[i]=s[i-1]+num[i];
	}
}
inline int FindMax()
{
	int ans=-0x3f3f3f3f;
	Q.push_back(0);
	for(int i=1;i<=n;i++)
	{
		while(!Q.empty()&&Q.front()<i-m)Q.pop_front();
		ans=max(ans,s[i]-s[Q.front()]);
		while(!Q.empty()&&s[Q.back()]>=s[i])Q.pop_back();
		Q.push_back(i);
	}
	return ans;
}
int main()
{
	freopen("test.in","r",stdin);
	freopen("test.out","w",stdout);
	input();
	printf("%d\n",FindMax());
	return 0;
}