1 建立測試圖（鄰接矩陣和鄰接表儲存形式）

首先建立一個圖用於後續程式碼的測試，在此以無向圖為例，且所有邊的權值都為1。儲存方式分別為鄰接矩陣和鄰接表（見上一篇介紹）

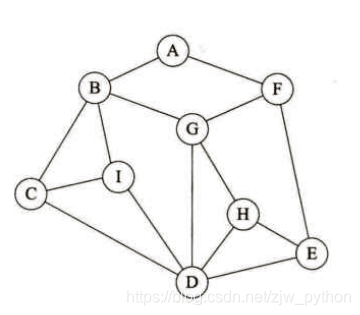
鄰接矩陣：

class Graph{
	constructor(v,vr){
		let len = v.length
		this.vexs = [].slice.apply(v);
		let arcs = [];
		for (let i=0;i<len;i++){
			arcs[i] = new Array(len);
			for (let j=0;j<len;j++){
				arcs[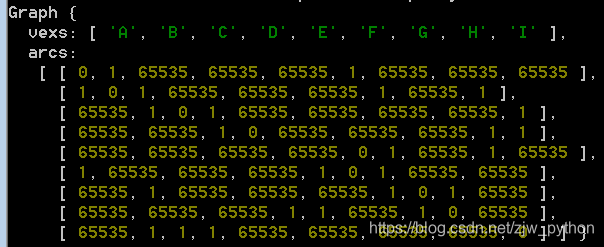
 
i][j] = i===j ? 0 : 65535;
			}
		}
		for (let arc of vr){
			let v1 = v.indexOf(arc[0]);
			let v2 = v.indexOf(arc[1]);
			arcs[v1][v2] = arcs[v2][v1] = arc[2] || 1;
		}
		this.arcs = arcs;
	}

}

let a = new Graph(['A','B','C','D','E','F','G','H','I'],[['A','B',1],['A','F',1],['B','G',1],['F','G',1]
 
,['B','C',1],['B','I',1],['G','H',1],['C','I',1],['I','D',1],['H','D',1],['F','E',1],['H','E',1],['C','D',1]]);
console.log(a);

鄰接表：

class vex{
	constructor(value){
		this.data = value;
		this.firstEdge = null;
	}

}

class adjvex{
	constructor(node,weight){
		this.node = node;
		this.weight =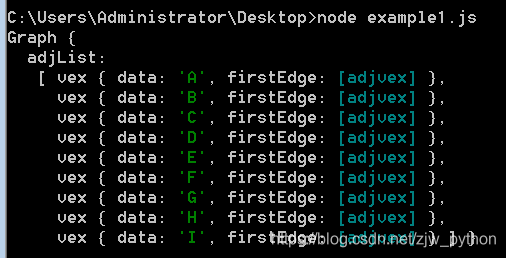
 
 weight;
		this.next = null;
	}
}

class Graph{
	constructor(v,vr){
		let len = v.length;
		let vexs = new Array(len);
		let v1=0,v2=0;
		let newvex = null;
		for (let i=0;i<len;i++){
			vexs[i] = new vex(v[i]);
		}
		for (let arc of vr){
			v1 = v.indexOf(arc[0]);
			v2 = v.indexOf(arc[1]);

			newvex = new adjvex(v1,arc[2]);
			newvex.next = vexs[v2].firstEdge;
			vexs[v2].firstEdge = newvex;

			newvex = new adjvex(v2,arc[2]);
			newvex.next = vexs[v1].firstEdge;
			vexs[v1].firstEdge = newvex;
		}
		this.adjList = vexs;
	}
}

let a = new Graph(['A','B','C','D','E','F','G','H','I'],[['A','B',1],['A','F',1],['B','G',1],['F','G',1],['B','C',1],['B','I',1],['G','H',1],['C','I',1],['I','D',1],['H','D',1],['F','E',1],['H','E',1],['C','D',1]]);
console.log(a);

2 深度優先遍歷

深度優先遍歷是一個遞迴過程，其從圖中某個頂點v出發，訪問此頂點，然後從v的未被訪問的鄰接點出發，深度優先遍歷圖，直至圖中所有點都被訪問到，類似於樹的前序遍歷。

鄰接矩陣：

function DFSTraverse(G){
	let visited = new Array(G.vexs.length);  //用於標記頂點是否被訪問過
	for (let i=0;i<G.vexs.length;i++){   //初始化
		visited[i] = false;
	}
	for (let i=0;i<G.vexs.length;i++){   //從第一個點開始遞迴訪問
		if (visited[i] === false){
			visited[i] = true;
			DFS(i);
		}
	}

	function DFS(i){
		console.log(G.vexs[i]);
		for (let j=0;j<G.vexs.length;j++){
			if (G.arcs[i][j] === 1 && visited[j] === false){  //訪問未訪問過的鄰接點
				visited[j] = true;
				DFS(j);
			}
		}
	}
}

鄰接表：

function DFSTraverse(G){
	let visited = new Array(G.adjList.length);   //用於標記頂點是否被訪問過
	for (let i=0;i<G.adjList.length;i++){   //初始化
		visited[i] = false;
	}
	for (let i=0;i<G.adjList.length;i++){   //從第一個點開始遞迴訪問
		if (visited[i] === false){
			visited[i] = true;
			DFS(i);
		}
	}

	function DFS(i){
		console.log(G.adjList[i].data);
		let adjvex = G.adjList[i].firstEdge;
		while(adjvex){
			if (visited[adjvex.node] === false){   //訪問未訪問過的鄰接點
				visited[adjvex.node] = true;
				DFS(adjvex.node);
			}
			adjvex = adjvex.next;
		}
	}
}

3 廣度優先遍歷

廣度優先遍歷類似於樹的層序遍歷，其從圖中某頂點v出發，訪問了v之後一次訪問v的各個未曾訪問過的鄰接點，然後分別從這些鄰接點出發依次訪問它們的鄰接點，且先被訪問的頂點的鄰接點先於後被訪問的頂點的鄰接點，直至圖中所有頂點都被訪問。
鄰接矩陣：

function BFSTraverse(G){
	let queue = [];   //使用佇列進行層序遍歷
	let visited = new Array(G.vexs.length);
	let vexnum = 0;
	for (let i=0;i<G.vexs.length;i++){
		visited[i] = false;
	}
	for (let i=0;i<G.vexs.length;i++){
		if (visited[i] === false){
			visited[i] = true;
			queue.push(i);
			while(queue.length > 0){
				vexnum = queue.shift();    //彈出佇列頭部序號，並訪問節點
				console.log(G.vexs[vexnum]);
				for (let j=0;j<G.vexs.length;j++){   //將當前節點未訪問過的的鄰接點序號推入佇列
					if (G.arcs[vexnum][j] === 1 && visited[j] === false){
						visited[j] = true;
						queue.push(j);
					}
				}
			}
		}	
	}
}

鄰接表：

function  BFSTraverse(G){
	let queue = [];
	let visited = new Array(G.adjList.length);
	let vexnum = 0;
	let adjvex = null;
	for (let i=0;i<G.adjList.length;i++){
		visited[i] = false;
	}
	for (let i=0;i<G.adjList.length;i++){
		if (visited[i] === false){
			visited[i] = true;
			queue.push(i);
		}
		while(queue.length > 0){
			vexnum = queue.shift();    //彈出佇列頭部序號，並訪問節點
			console.log(G.adjList[vexnum].data);
			adjvex = G.adjList[vexnum].firstEdge;
			while(adjvex){  		//將當前節點未訪問過的的鄰接點序號推入佇列
				if (visited[adjvex.node] === false){
					visited[adjvex.node] = true;
					queue.push(adjvex.node);
				}
				adjvex = adjvex.next;
			}
		}
	}
}