深度學習中的Batch Normalization
在看 ladder network(https://arxiv.org/pdf/1507.02672v2.pdf) 時初次遇到batch normalization(BN). 文中說BN能加速收斂等好處,但是並不理解,然後就在網上搜了些關於BN的資料。
看了知乎上關於深度學習中 Batch Normalization為什麼效果好? 和CSDN上一個關於Batch Normalization 的學習筆記,總算對BN有一定的瞭解了。這裡只是總結一下BN的具體操作流程,對於BN更深層次的理解,為什麼要BN,BN是否真的有效也還在持續學習和實驗中。
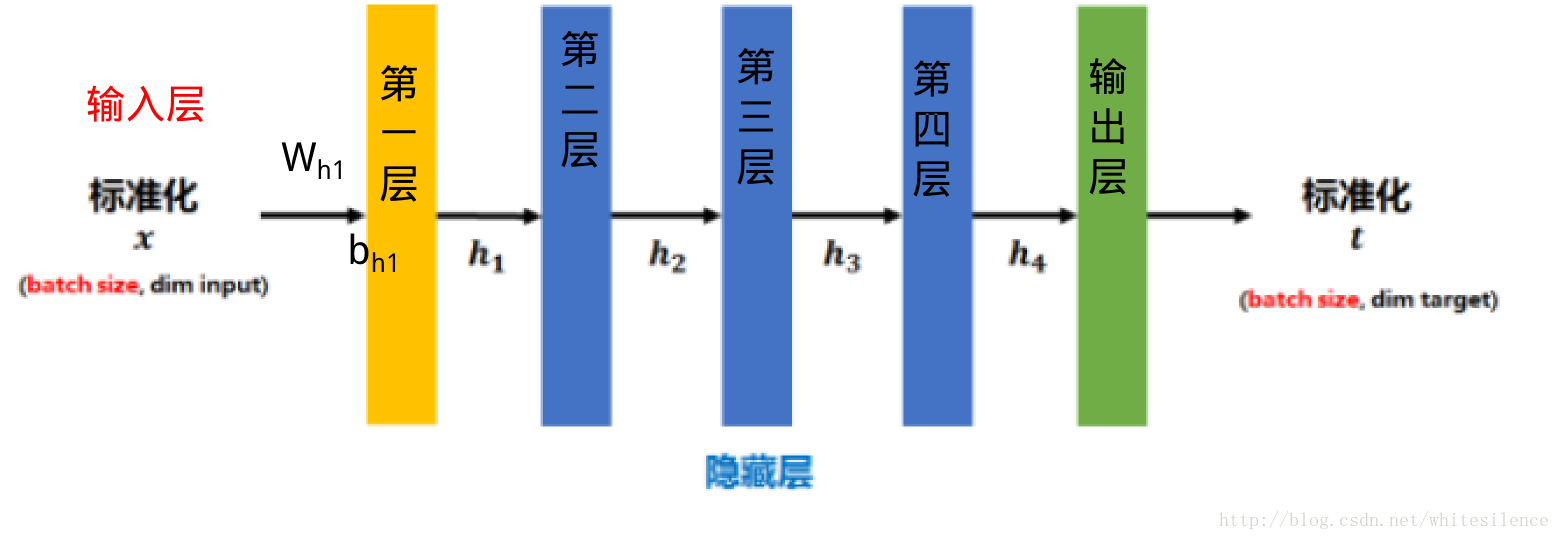
BN就是在神經網路的訓練過程中對每層的輸入資料加一個標準化處理。
傳統的神經網路,只是在將樣本
標準化後的
1. 矩陣
將
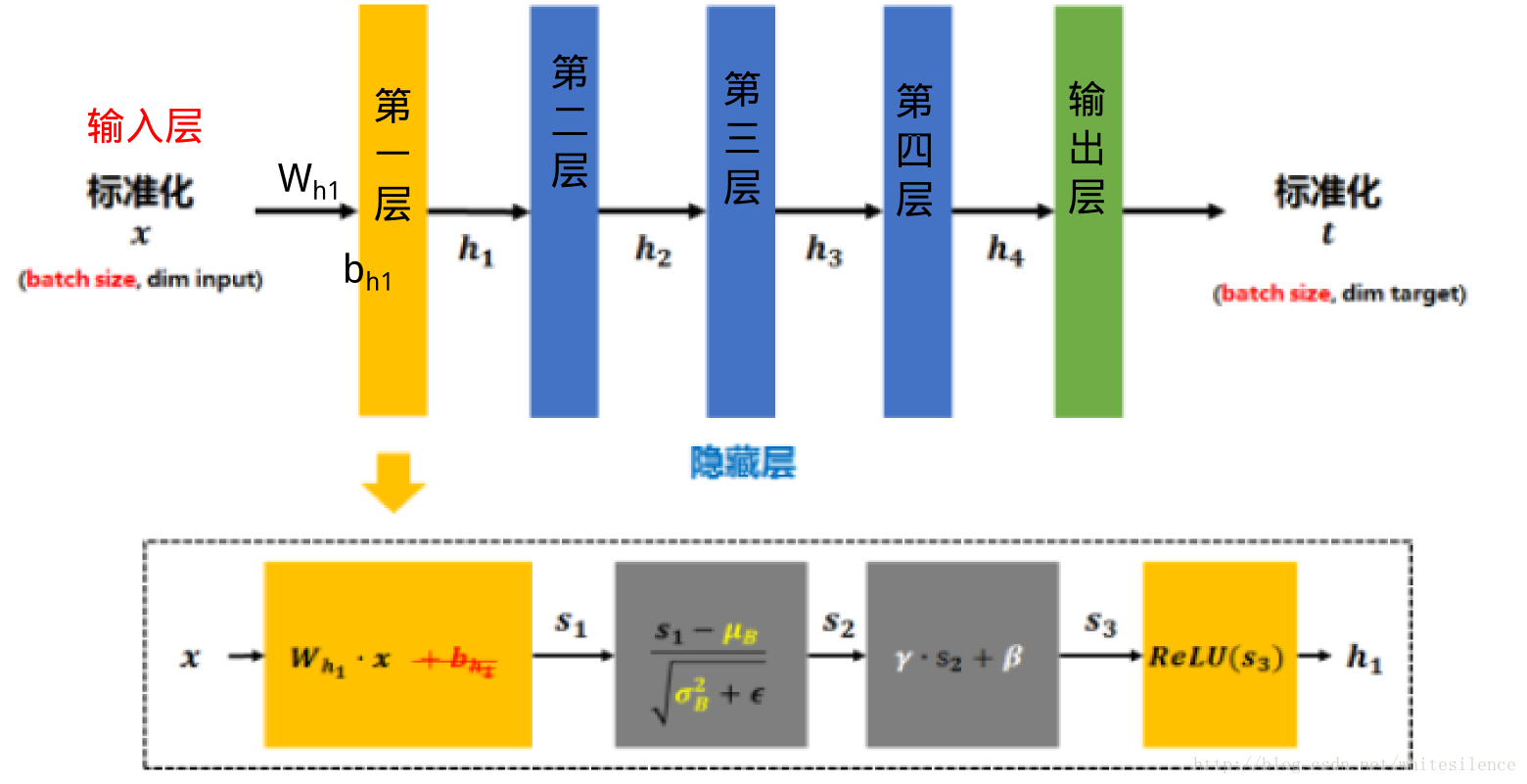
s1 再減去batch的平均值μB ,併除以batch的標準差σ2B+ϵ−−−−− 得到√s2 .ϵ 是為了避免除數為0時所使用的微小正數。
其中μB=1m∑mi=0Wh1xi
σ2B=1m∑mi=0(Wh1xi−μB)2
(注:由於這樣做後s2 基本會被限制在正態分佈下,使得網路的表達能力下降。為解決該問題,引入兩個新的引數:γ ,β .γ 和β 是在訓練時網路自己學習得到的。)將
s2 乘以γ 調整數值大小,再加上β 增加偏移後得到s3 s3 經過啟用函式後得到h1
需要注意的是,上述的計算方法用於在訓練過程中。在測試時,所使用的
在看具體程式碼之前,先來看兩個求平均值函式的用法:
mean, variance = tf.nn.moments(x, axes, name=None, keep_dims=False)
這個函式的輸入引數x表示樣本,形如[batchsize, height, width, kernels]
axes表示在哪個維度上求解,是個list
函式輸出均值和方差
'''
batch = np.array(np.random.randint(1, 100, [10, 5]))開始這裡沒有定義資料型別,batch的dtype=int64,導致後面sess.run([mm,vv])時老報InvalidArgumentError錯誤,原因是tf.nn.moments中的計算要求引數是float的
'''
batch = np.array(np.random.randint(1, 100, [10, 5]),dtype=np.float64)
mm, vv=tf.nn.moments(batch,axes=[0])#按維度0求均值和方差
#mm, vv=tf.nn.moments(batch,axes=[0,1])求所有資料的平均值和方差
sess = tf.Session()
print batch
print sess.run([mm, vv])#一定要注意引數型別
sess.close()輸出結果:
[[ 53. 9. 67. 30. 69.]
[ 79. 25. 7. 80. 16.]
[ 77. 67. 60. 30. 85.]
[ 45. 14. 92. 12. 67.]
[ 32. 98. 70. 98. 48.]
[ 45. 89. 73. 73. 80.]
[ 35. 67. 21. 77. 63.]
[ 24. 33. 56. 85. 17.]
[ 88. 43. 58. 82. 59.]
[ 53. 23. 34. 4. 33.]]
[array([ 53.1, 46.8, 53.8, 57.1, 53.7]), array([ 421.09, 896.96, 598.36, 1056.69, 542.61])]ema = tf.train.ExponentialMovingAverage(decay) 求滑動平均值需要提供一個衰減率。該衰減率用於控制模型更新的速度,ExponentialMovingAverage 對每一個(待更新訓練學習的)變數(variable)都會維護一個影子變數(shadow variable)。影子變數的初始值就是這個變數的初始值,
shadow_variable=decay×shadow_variable+(1−decay)×variable
由上述公式可知, decay 控制著模型更新的速度,越大越趨於穩定。實際運用中,decay 一般會設定為十分接近 1 的常數(0.99或0.999)。為了使得模型在訓練的初始階段更新得更快,ExponentialMovingAverage 還提供了 num_updates 引數來動態設定 decay 的大小:
對於滑動平均值我是這樣理解的(也不知道對不對,如果有覺得錯了的地方希望能幫忙指正)
假設有一串時間序列
作者:張俊林,新浪微博AI Lab擔任資深演算法專家
注:小白想系統整理一些深度學習相關的理論知識,如有侵權請聯絡刪除。
Batch Normalization(簡稱BN)自從提出之後,因為效果特別好,很快被作為深度學習的標準工具應用在了各種場合。BN大法雖然好,但是 來源:https://www.chainnews.com/articles/504060702149.htm
機器之心專欄
作者:張俊林
Batch Normalization (簡稱 BN)自從提出之後,因為效果特別好,很快被作為深度學習的標準工具應用在了各種場合。BN 大法雖然好,但是也存
參考:https://www.cnblogs.com/guoyaohua/p/8724433.html
引入原因:深度網路訓練過程中,每一層的引數都會不斷變化,很可能導致每一層的輸出(即對下一層的輸入)的分佈發生變化,因此導致模型收斂變慢,(本質原因:輸出逐漸向左右兩端移動,導致曲線平緩,比
“深度神經網路模型訓練之難眾所周知,其中一個重要的現象就是 Internal Covariate cal ati 階段 idt 影響 ima 隨機梯度下降 新的 left
原文鏈接:https://www.cnblogs.com/Luv-GEM/p/10756382.html
在機器學習領域中,有一個重要的假設:獨立同分布假設,也就是假設訓練數據和測試數據是
在看 ladder network(https://arxiv.org/pdf/1507.02672v2.pdf) 時初次遇到batch normalization(BN). 文中說BN能加速收斂等好處,但是並不理解,然後就在網上搜了些關於BN的資料。
看了知
由於深度學習的網格很大,用來訓練的資料集也很大。因此不可能一下子將所有資料集都輸入到網路中,便引入了batch_size的概念,下面總結自己兩種常用的呼叫batch的方法
1、使用TensorFlow, tf.train.batch()。
2、
offset = (offset
(1)iteration:表示1次迭代(也叫training step),每次迭代更新1次網路結構的引數;
(2)batch-size:1次迭代所使用的樣本量;
(3)epoch:1個epoch表示過了1遍訓練集中的所有樣本。
值得注意的是,在深度學習領域中,常用帶mini-batch的 Batch_size引數的作用:決定了下降的方向
極端一:
batch_size為全資料集(Full Batch Learning):
好處:
1.由全資料集確定的方向能夠更好地代表樣本總體,從而更準確地朝向極值所在的方向。
2.由於不同權重的梯度值差別巨大,因此選擇一個全域性的學習率很困難。Ful
兩者的論文:
Dropout:http://www.jmlr.org/papers/volume15/srivastava14a/srivastava14a.pdf
Layer Normaliza
1,批量梯度下降法(Batch Gradient Descent) :在更新引數時都使用所有的樣本來進行更新。
優點:全域性最優解,能保證每一次更新權值,都能降低損失函式;易於並行實現。
缺點:當樣本數目很多時,訓練過程會很慢。
2,隨機梯度下降法(Stoch
機器學習的學習過程基於概率和統計學,學習到的知識能用於其它資料的一個基本假設是獨立同分布(IID),因此把資料變成同分布是很有必要的。
A.權重歸一化: WN
不歸一化特徵,而是歸一化權重。
B.特徵歸一化: BN、LN、IN、GN、SN
歸一化操作
BN、LN、IN、GN這
在進行深度學習的過程中,我們經常會遇到一些自己不懂的概念和術語,比如,softmax, batch,min-batch,iterations,epoch,那麼如何快速和容易的理解這些術語呢? 因為筆者也是深度學習的初學者,所以筆者在學習和瀏覽文章的過程中,把一些自己不太容易和
在剛開始學習使用TF的過程中,我不是很理解什麼是“batch”。也經常有人問,到底minibatch是幹什麼的?
然而這是一個在TensorFlow中,或者說很多DL的框架中很常見的詞。
這個解釋我覺得比較貼切也比較容易理解。引用如下:
深度學習的優化演算法,說白了就是梯度 c51 進行 ros batch num 簡單的 oat 深度學習 repr
目錄
1. 什麽是正則化?
2. 正則化如何減少過擬合?
3. 深度學習中的各種正則化技術:
L2和L1正則化
Dropout
數據增強(Data augmentation)
提前停止(Ear 範圍 SM 全連接 判斷 contact con 發展 .dsp length 卷積可能是現在深入學習中最重要的概念。卷積網絡和卷積網絡將深度學習推向了幾乎所有機器學習任務的最前沿。但是,卷積如此強大呢?它是如何工作的?在這篇博客文章中,我將解釋卷積並將其與其他概念聯系起來 line question 代價函數 online 由於 數據 減少 使用 矛盾 5.4.1 關於深度學習中的batch_size
batch_size可以理解為批處理參數,它的極限值為訓練集樣本總數,當數據量比較少時,可以將batch_size值設置為全數據集(Full
轉
深度學習中 GPU 和視訊記憶體分析
2017年12月21日 14:05:01
lien0906
閱讀數:5941
更多
目錄
1. Problem
I. Introduction
II. Analysis
2. Address the problem
I. Batch normalization 及其問題
II. 梯度修正及其問題
III. Key alg
選自MachineLearningMastery
作者:Jason Brownlee
機器之心編譯
參與:Nurhachu Null、劉曉坤
本文介紹了遷移學習的基本概念,以及該方法在深度學習中的應用,引導構建預測模型的時候使用遷移學習的基本策略。
遷移學習是一種機器學習 相關推薦
深度學習中的Normalization模型
[優化]深度學習中的 Normalization 模型
【深度學習】batch normalization
詳解深度學習中的Normalization,不只是BN(2)
深度學習之Batch Normalization
深度學習中的Batch Normalization
關於在深度學習中訓練資料集的batch的經驗總結
深度學習中的 epoch iteration batch-size
深度學習中的batch的大小對學習效果的影響
深度學習中Dropout和Layer Normalization技術的使用
深度學習中的三種梯度下降方式:批量(batch),隨機(stochastic),小批量(mini-batch)
深度學習中的歸一化(normalization)和正則化(regularization)
[6]深度學習和Keras---- 深度學習中的一些難理解的基礎概念:softmax, batch,min-batch,iterations,epoch,SGD
深度學習中常見的相關概念及TensorFlow中的batch和minibatch
資深程序員帶你玩轉深度學習中的正則化技術(附Python代碼)!
卷積在深度學習中的作用(轉自http://timdettmers.com/2015/03/26/convolution-deep-learning/)
關於深度學習中的batch_size
深度學習中 GPU 和視訊記憶體分析 深度學習中 GPU 和視訊記憶體分析
論文學習:Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift
【遷移學習】簡述遷移學習在深度學習中的應用