不知道你是否看過我之前的文章，如果看了的話，你會認為很爛，然後判斷這篇部落格也是很大程度上是很爛的，如果這樣的，很幸運，那你使用了貝葉斯思維方式來進行思考問題了。
    學了這麼多年貝葉斯公式，不是很瞭解貝葉斯公式，但是今天和師兄去聊似然函式的時候，聊到了貝葉斯公式，感覺可以去解釋人生當中做的一些判斷。下面是這篇部落格的要講的三個問題
    1.頻率學派和貝葉斯學派的區別？
    2.什麼叫似然函式，它從直覺意義上表示什麼意思，為什麼要進行“最大”似然估計？為什麼在最優化的時候需要取log？
    3.貝葉斯公式感悟？

一：頻率學派和貝葉斯學派的區別？
    首先講下，在概率統計上，有兩個學派，一個是頻率學派，一個是貝葉斯學派，“最大”似然是頻率學派提出的。為什麼將最大用引號呢，因為似然函式是兩個學派共有的。那頻率學派和貝葉斯學派有什麼根本的區別呢？
    你從名字就可以看出來他們關心的就是我有多大把握去圈出那個“唯一”的真實引數。而貝葉斯學派恰恰相反，他們關心引數空間裡的“每一個值”，因為他們覺得我們又沒有上帝視角，怎麼可能知道哪個值是正確的呢？所以引數空間裡的每個值都有可能是真實模型使用的值，區別只是概率不同而已。最好詮釋這種差別的例子就是想象如果你的後驗分佈是雙峰的，頻率學派的方法會去選這兩個峰當中較高的那一個對應的值作為他們的最好猜測，而貝葉斯學派則會同時報告這兩個值，並給出對應的概率。
    在二十世紀之前，頻率學派發展很迅速很快佔據了概率統計半壁江山，現在很多本科教材大量的篇幅使用的都是頻率學派的認識。而貝葉斯學派的東西只是一筆帶過，很大程度上是因為在貝葉斯學派中很多推斷都是基於概率分佈，直到上世紀90年代依靠電子計算機的迅速發展，以及抽樣演算法的進步（GIBBS取樣）使得對於任何模型任何先驗分佈都可以有效地求出後驗分佈，貝葉斯學派才重新回到人們的視線當中。

二：.什麼叫似然函式，它從直覺意義上表示什麼意思，為什麼要進行“最大”似然估計？為什麼在最優化的時候需要取log?
2.1  什麼叫似然函式？為什麼進行最大似然估計？
    似然的意思是可能性，它的意思和possibility的意思是一樣的。
給定輸出x時，關於引數θ的似然函式L(θ|x)（在數值上）等於給定引數θ後變數X的概率：

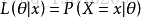
    首先它表示的是所有樣本同時發生的概率，而為什麼需要最大的呢，因為當你樣本已經拿到你手上了，即表示這個事件已經發生了，那麼最大化，這個事件的概率，從而得到引數θ，在直覺上是有道理的。
2.2 為什麼需要取log?

    那麼為什麼在最優化的時候需要取log呢？有兩點原因。
    1.為了求解簡單，在求導的時候。
    2.為了避免數值的下溢。因為L(θ|x)是由很多概率相乘，而每個概率都是小於一的，如果樣本量很大的時候，那麼很容易導致L(θ|x)非常非常的小。
2.3 一個栗子
    舉個栗子，在歷史上有很多人比價有探（zhi）索(zhang)性,有很多數學家做過相關的實驗，比如：
德摩根： 實驗次數：4092 正面次數：2048
蒲豐： 實驗次數：4040 正面次數：2048
費勒： 實驗次數：10000 正面次數：4979
羅曼諾夫斯基 ：實驗次數：80640 正面次數：39699
    上面幾位老哥，當然要數羅曼諾夫斯基，這位老哥擲了80640次，很執著，為了探索冥冥之中操縱自然規律的上帝。
    下面我們用matlab求出，羅曼諾夫斯基擲了80640次，的似然函式，及相應的最大值!!!
求解：p:表示正面的概率，1-p:表示反面的概率。

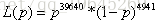
對似然函式取log得到如下公式

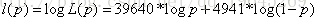
用matlab畫圖如下：

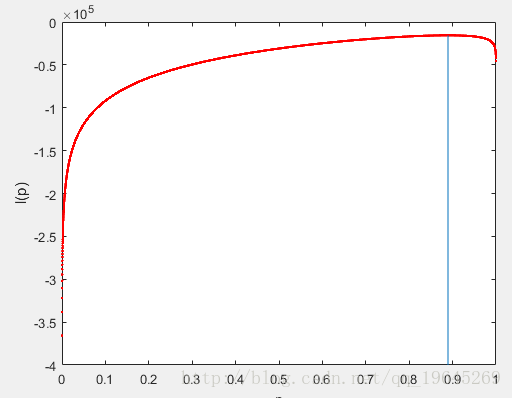
    通過計算可以得出，使上式最大的p=0.8894
    原因分析：那麼就有人疑問了，為什麼會出現這樣的結論呢，筆者猜測可能是硬幣不均勻可能導致的。但是求解似然函式的步驟就是這樣的。
三：貝葉斯公式感悟?

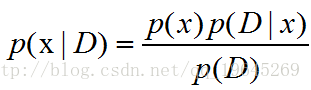
    首先看下這個公式，如果把x看做是你對一件事或者是你的人生，那麼p(x)就表示你原先的世界觀或者是對事情的理解，而p(D|x)表示你在生活中遇到的事情，p(x)p(D|x)就表示日常生活中你經歷的事情，然後去對你之前的世界觀進行更新，從而得到最後的世界觀或者是對一件事情的認識。所以嘛，當你在生活中如果一件事情你經歷了很多遍，不管是好的還是壞的，那麼你對待這件事情就有很多感悟，從而來更新你對待事物的看法，並且可以理解到這件事情的本質，從而可以得到一個很好的判斷。
    我覺得現在每個人都應該用貝葉斯學派的思想去對待生活，對生活看淡，對事情看淡，從而可以做到寵辱不驚一個人。所以嘛，年輕的時候出去闖闖還是蠻有道理的。