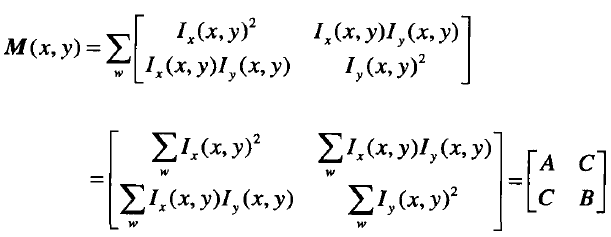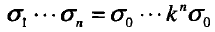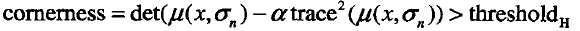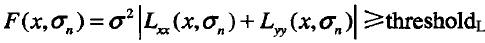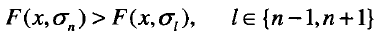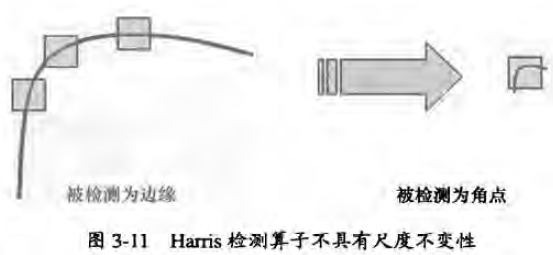
Harris角點的不變性與侷限性：

1. 由於Harris角點檢測涉及到了影象的一階微分運算，因此Harris角點對影象亮度和對比度具有不變性；
2. 同時角點檢測利用的是二階矩的特徵值，對應於橢圓區域的長軸和短軸的倒數，因此具有旋轉不變性。

但是其不具備尺度不變性，下圖就可以說明這種情況

具有尺度不變性的Harris角點檢測：

相對普通的Harris角點檢測，其發生改變的主要在二階矩的表現形式上：
具備尺度不變性Harris的二階矩：

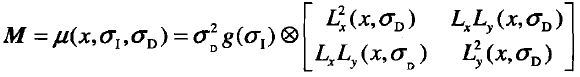
普通的Harris的二階矩：

兩者對比，前者在後者的基礎上增加了兩個因子，積分尺度因子和微分尺度因子。前者是讓影象通過含有微分尺度因子高斯核函式進行濾波處理後再進行普通的Harris的二階矩的求解處理，緊接著利用含有積分尺度因子的高斯核函式與之卷積得到含有尺度因子的二階矩表現形式。
在這裡討論一下，積分尺度因子和微分尺度因子的具體含義：
微分尺度因子，他是決定角點附近微分值變化的變數，我覺得主要就是為了消除噪聲對結果的影響；
積分尺度因子，他是決定當前尺度的變數，這個和尺度空間的建立的一致的；可以知道積分尺度因子大於微分尺度因子

具體流程：

1. 尺度不變性，當然得建立尺度空間。因此選定一組尺度值：
   
   然後大牛Mikolajczyk對於微分尺度的選取一般是0.7倍的積分尺度。在每一個尺度下，計算其角點響應：
   
   為了避免角點過於集中重疊，可以進行非最大值抑制，即在每個角點響應大於閾值的候選點的8鄰域內進行角點響應最大值的搜尋。

2. 由於位置空間的候選點不一定是在尺度空間也能成為候選點，對於位置空間的每個候選點進行拉普拉斯響應計算：
   
   然後和其鄰域的兩個尺度空間的位置點的拉普拉斯響應值進行比較，滿足下式說明該點也是尺度空間的候選點：
   

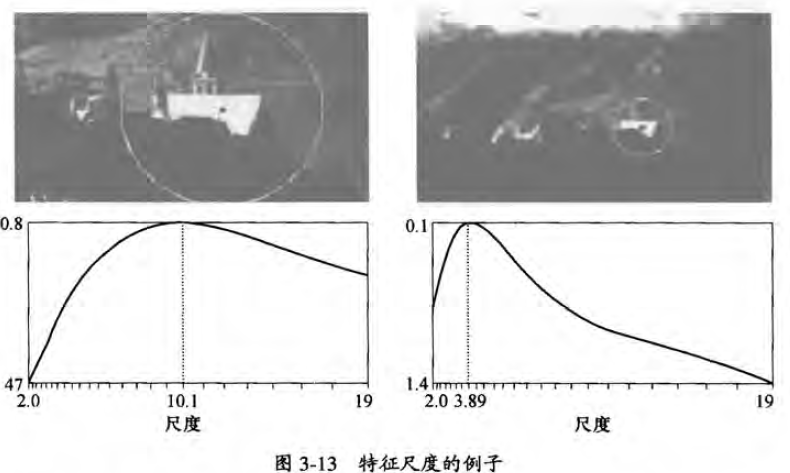
最後給大家看一個具備尺度不變性的例子：