數字影象處理學習筆記(1)——傅立葉變換在影象處理中的應用
1.理解二維傅立葉變換的定義
1.1二維傅立葉變換
二維Fourier變換:
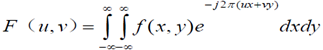
逆變換:
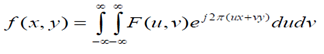
1.2二維離散傅立葉變換
一個影象尺寸為M×N的 函式的離散傅立葉變換由以下等式給出:
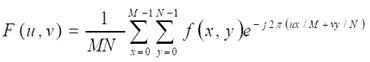
其中 和。其中變數u和v用於確定它們的頻率,頻域系統是由所張成的座標系,其中和用做(頻率)變數。空間域是由f(x,y)所張成的座標系。可以得到頻譜系統在頻譜圖四角處沿和方向的頻譜分量均為0。
離散傅立葉逆變換由下式給出:
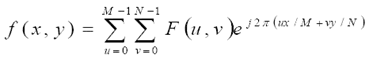
令R和I分別表示F的實部和需部,則傅立葉頻譜,相位角,功率譜(幅度)定義如下:
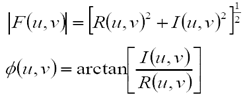

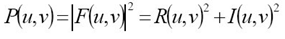
1.3用FFT計算二維離散傅立葉變換
二維離散傅立葉變換的定義為:
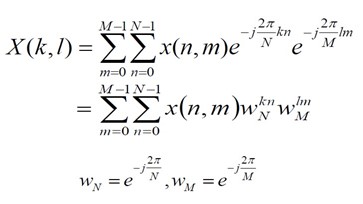
二維離散傅立葉變換可通過兩次一維離散傅立葉變換來實現:
1)作一維N點DFT(對每個m做一次,共M次)
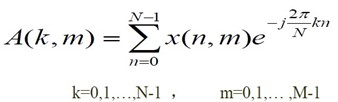
2)作M點的DFT(對每個k做一次,共N次)
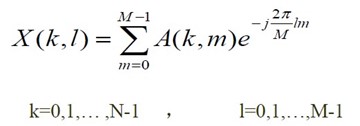

這兩次離散傅立葉變換都可以用快速演算法求得,若M和N都是2的冪,則可使用基二FFT演算法,所需要乘法次數為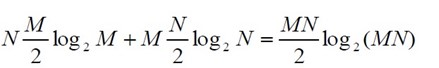
而直接計算二維離散傅立葉變換所需的乘法次數為(M+N)MN,當M和N比較大時用用FFT運算,可節約很多運算量。
1.3影象傅立葉變換的物理意義
影象的頻率是表徵影象中灰度變化劇烈程度的指標,是灰度在平面空間上的梯度。如:大面積的沙漠在影象中是一片灰度變化緩慢的區域,對應的頻率值很低;而對於地表屬性變換劇烈的邊緣區域在影象中是一片灰度變化劇烈的區域,對應的頻率值較高。傅立葉變換在實際中有非常明顯的物理意義,設f是一個能量有限的模擬訊號,則其傅立葉變換就表示f的頻譜。從純粹的數學意義上看,傅立葉變換是將一個函式轉換為一系列周期函式來處理的。從物理效果看,傅立葉變換是將影象從空間域轉換到頻率域,其逆變換是將影象從頻率域轉換到空間域。換句話說,傅立葉變換的物理意義是將影象的灰度分佈函式變換為影象的頻率分佈函式。
傅立葉頻譜圖上我們看到的明暗不一的亮點,其意義是指影象上某一點與鄰域點差異的強弱,即梯度的大小,也即該點的頻率的大小(可以這麼理解,影象中的低頻部分指低梯度的點,高頻部分相反)。一般來講,梯度大則該點的亮度強,否則該點亮度弱。這樣通過觀察傅立葉變換後的頻譜圖,也叫功率圖,我們就可以直觀地看出影象的能量分佈:如果頻譜圖中暗的點數更多,那麼實際影象是比較柔和的(因為各點與鄰域差異都不大,梯度相對較小);反之,如果頻譜圖中亮的點數多,那麼實際影象一定是尖銳的、邊界分明且邊界兩邊畫素差異較大的。
對頻譜移頻到原點以後,可以看出影象的頻率分佈是以原點為圓心,對稱分佈的。將頻譜移頻到圓心除了可以清晰地看出影象頻率分佈以外,還有一個好處,它可以分離出有周期性規律的干擾訊號,比如正弦干擾。一幅頻譜圖如果帶有正弦干擾,移頻到原點上就可以看出,除了中心以外還存在以另一點為中心、對稱分佈的亮點集合,這個集合就是干擾噪音產生的。這時可以很直觀的通過在該位置放置帶阻濾波器消除干擾。
2.二維傅立葉變換有哪些性質
2.1二維離散傅立葉變換的性質
1)分離性
二維離散傅立葉變換具有分離性

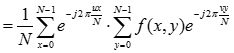
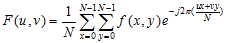
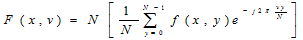
分離性質的主要優點是可藉助一系列一維傅立葉變換分兩步求得。第1步,沿著的每一行取變換,將其結果乘以1/N,取得二維函式;第2步,沿著的每一列取變換,再將結果乘以1/N,就得到了。這種方法是先行後列。如果採用先列後行的順序,其結果相同。
如圖:

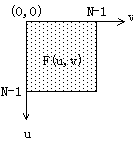
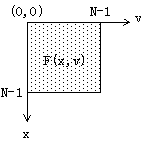
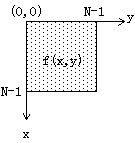

對逆變換f(x,y)也可以類似地分兩步進行。
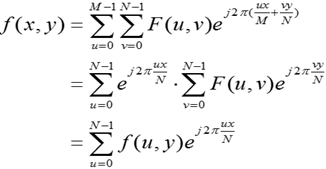
2)平移性
傅立葉變換和逆變換對的位移性質是指:


由乘以指數項並取其乘積的傅立葉變換,使頻率平面的原點位移至。同樣地,以指數項乘以並取其反變換,將空間域平面的原點位移至當N/2時,指數項為:

即為
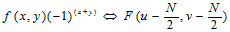
這樣,用(x+y)乘以就可以將的傅立葉變換原點移動到N*N頻率方陣的中心,這樣才能看到整個譜圖。另外,對的平移不影響其傅立葉變換的幅值。
此外,與連續二維傅立葉變換一樣,二維離散傅立葉變換也具有周期性、共軛對稱性、線性、旋轉性、相關定理、卷積定理、比例性等性質。這些性質在分析及處理影象時有重要意義。
2.2二維離散傅立葉變換影象性質
1、影象經過二維傅立葉變換後,其變換系數矩陣具有如下性質:若變換矩陣原點設在中心,其頻譜能量集中分佈在變換系數短陣的中心附近(圖中陰影區)。若所用的二維傅立葉變換矩陣的原點設在左上角,那麼影象訊號能量將集中在係數矩陣的四個角上。這是由二維傅立葉變換本身性質決定的。同時也表明一股影象能量集中低頻區域。
2、影象灰度變化緩慢的區域,對應它變換後的低頻分量部分;影象灰度呈階躍變化的區域,對應變換後的高頻分量部分。除顆粒噪音外,影象細節的邊緣、輪廓處都是灰度變化突變區域,它們都具有變換後的高頻分量特徵。
3.任給一幅影象,對其進行二維傅立葉變換和逆變換

|
原圖 |
二維傅立葉變換 |
|
逆變換 |
頻譜圖 |

| 原圖 | 加入高斯噪聲 | 計入椒鹽噪聲 |
| 對高斯噪聲中值濾波 | 對椒鹽噪聲中值濾波 | |
| 對高斯噪聲算術均值濾波 | 對椒鹽噪聲算術均值濾波 |
4.附錄
4.1matlab程式碼
1)DEMO1[i,lcmp]=imread('F:/123.jpg');%=======讀取影象 顯示影象
subplot(2,2,1),imshow(i,lcmp);
title('original');
ii=im2double(i); %=====將影象矩陣型別轉換為double(影象計算很多是不能用整型的),沒有這個會報錯!! ,如果不用這個就必須轉化為灰度圖!
i1 = fft2(ii); %======傅立葉變換
i2 =fftshift(i1); %======將變換的頻率影象四角移動到中心(原來良的部分在四角 現在移動中心,便於後面的處理)
i3=log(abs(i2)); %=====顯示中心低頻部分,加對數是為了更好的顯示
subplot(2,2,2),imshow(i3,[]);
title('Fourier');
map=colormap(lcmp); %===取色譜
imwrite(i3,map,'f:/ffttank.bmp'); %===將上面i3輸入到ffttank檔案中
i5 = real(ifft2(ifftshift(i2))); %===頻域的圖反變換到空域 並取實部
i6 = im2uint8(mat2gray(i5)); %===取其灰度圖
imwrite(i6,map,'f:/tank2.bmp','bmp'); %===利用灰度圖和原來取得顏色模板 還原影象
subplot(2,2,3),imshow(i6);
title('anti-Fourier');
i7=rgb2gray(i);
i8=fft2(i7);%===對灰色圖才能歸一化。因為那是2維矩陣,彩色圖是3維矩陣,需要轉化為2維灰圖
m=fftshift(i8); %直流分量移到頻譜中心
%RR=real(m); %取傅立葉變換的實部
%II=imag(m); %取傅立葉變換的虛部
A=abs(m);%計算頻譜幅值
%A=sqrt(RR.^2+II.^2);
A=(A-min(min(A)))/(max(max(A))-min(min(A)))*225; %歸一化
subplot(2,2,4),imshow(A); %顯示原影象
colorbar; %顯示影象的顏色條
title('FFT spectrum'); %影象命名m=imread('F:/123.jpg');
M=rgb2gray(m); %==濾波函式都是對二維灰度圖,Tif可直接濾波
subplot(3,3,1)
imshow(M);%顯示原始影象
title('original')
P1=imnoise(M,'gaussian',0.02); %加入高斯躁聲
subplot(3,3,2)
imshow(P1) %加入高斯躁聲後顯示影象
title('gaussian noise');
P2=imnoise(M,'salt & pepper',0.02); %=加入椒鹽躁聲
subplot(3,3,3)
imshow(P2) %%加入椒鹽躁聲後顯示影象
title('salt & pepper noise');
g=medfilt2(P1); %對高斯躁聲中值濾波
subplot(3,3,5)
imshow(g)
title('medfilter gaussian')
h=medfilt2(P2); %對椒鹽躁聲中值濾波
subplot(3,3,6)
imshow(h)
title('medfilter salt & pepper noise')
l=[1 1 1 %對高斯躁聲算術均值濾波
1 1 1
1 1 1];
l=l/9;
k=conv2(P1,l);
subplot(3,3,8)
imshow(k,[])
title('arithmeticfilter gaussian')
%對椒鹽躁聲算術均值濾波
d=conv2(P2,l);
subplot(3,3,9)
imshow(d,[])
title('arithmeticfilter salt & pepper noise')4.2參考文獻
[1]孟凡文, 吳祿慎.基於FTP的二維傅立葉變換的研究.鐳射與紅外.第38卷第9期 2008年9月
[2] 董健,鄧國輝,李金武. 基於二維傅立葉變換實現影象變換的研究. 福建電腦. 2015年第 9期
原文連結:http://www.cnblogs.com/tenderwx/p/5245859.html
