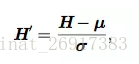一、深度學習中常用的調節引數

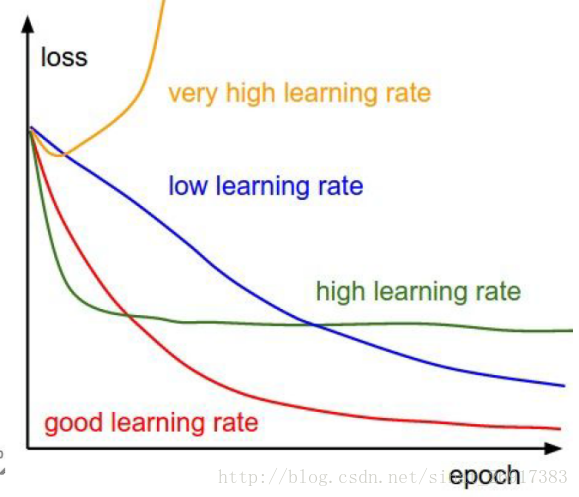
1、學習率

步長的選擇：你走的距離長短，越短當然不會錯過，但是耗時間。步長的選擇比較麻煩。步長越小，越容易得到區域性最優化（到了比較大的山谷，就出不去了），而大了會全域性最優

一般來說，前1000步，很大，0.1；到了後面，迭代次數增高，下降0.01，再多，然後再小一些。

2、權重

梯度消失的情況，就是當數值接近於正向∞，求導之後就更小的，約等於0，偏導為0
梯度爆炸，數值無限大

對於梯度消失現象：啟用函式
Sigmoid會發生梯度消失的情況，所以啟用函式一般不用，收斂不了了。Tanh(x)，沒解決梯度消失的問題。
ReLu Max(0,x)，比較好，代表Max門單元，解決了梯度消失的問題，而且起到了降維

權重初始化，可以隨機也可以一開始設定一定的圖形分佈，用高斯初始化

3、層數

越多，靈敏度越好，收斂地更好，啟用函式也越多，曲線的效能也更好
但是，神經元過擬合，並且計算量較大層數越多。在節點多的情況下一般會考慮：Drop-out
節點太多也不好，所以需要刪除一些無效的節點
但是去掉節點，這裡卻是隨機的，隨機去掉（30%-60%）的節點
注意：隨機的選擇，去掉一些節點。但是drop-out也不一定是避免過擬合
很常見。一般不drop-out一定會過擬合，有drop-out概率低一些

4、過擬合

上面的drop-out就算一種。其他過擬合可能也會使用：BN,batch normalization（歸一化）

在caffe操作時候，模型訓練中如何解決過擬合現象？

看到驗證集的資料趨於平穩，譬如第1000次之後，驗證集的loss平穩了，那麼就擷取1000次，把學習率降低為原來的0.1，拿來第10000次結果，修改檔案，繼續訓練。
.

5、Loss設計與觀察

一般來說分類就是Softmax, 迴歸就是L2的loss. 但是要注意loss的錯誤範圍(主要是迴歸), 你預測一個label是10000的值, 模型輸出0, 你算算這loss多大, 這還是單變數的情況下. 一般結果都是nan. 所以不僅僅輸入要做normalization, 輸出也要。
準確率雖然是評測指標, 但是訓練過程中還是要注意loss的. 你會發現有些情況下, 準確率是突變的, 原來一直是0, 可能保持上千迭代, 然後突然變1. 要是因為這個你提前中斷訓練了, 只有老天替你惋惜了. 而loss是不會有這麼詭異的情況發生的, 畢竟優化目標是loss.
對比訓練集和驗證集的loss。 判斷過擬合, 訓練是否足夠, 是否需要early stop的依據

二、caffe訓練時Loss變為nan的原因

本節轉載於公眾號平臺：極市平臺

1、梯度爆炸

原因：梯度變得非常大，使得學習過程難以繼續

現象：觀察log，注意每一輪迭代後的loss。loss隨著每輪迭代越來越大，最終超過了浮點型表示的範圍，就變成了NaN。
措施：
1. 減小solver.prototxt中的base_lr，至少減小一個數量級。如果有多個loss layer，需要找出哪個損失層導致了梯度爆炸，並在train_val.prototxt中減小該層的loss_weight，而非是減小通用的base_lr。
2. 設定clip gradient，用於限制過大的diff

2、不當的損失函式

原因：有時候損失層中loss的計算可能導致NaN的出現。比如，給InfogainLoss層（資訊熵損失）輸入沒有歸一化的值，使用帶有bug的自定義損失層等等。

現象：觀測訓練產生的log時一開始並不能看到異常，loss也在逐步的降低，但突然之間NaN就出現了。
措施：看看你是否能重現這個錯誤，在loss layer中加入一些輸出以進行除錯。
示例：有一次我使用的loss歸一化了batch中label錯誤的次數。如果某個label從未在batch中出現過，loss就會變成NaN。在這種情況下，可以用足夠大的batch來儘量避免這個錯誤。

3、不當的輸入

原因：輸入中就含有NaN。

現象：每當學習的過程中碰到這個錯誤的輸入，就會變成NaN。觀察log的時候也許不能察覺任何異常，loss逐步的降低，但突然間就變成NaN了。
措施：重整你的資料集，確保訓練集和驗證集裡面沒有損壞的圖片。除錯中你可以使用一個簡單的網路來讀取輸入層，有一個預設的loss，並過一遍所有輸入，如果其中有錯誤的輸入，這個預設的層也會產生NaN。
案例：有一次公司需要訓練一個模型，把標註好的圖片放在了七牛上，拉下來的時候發生了dns劫持，有一張圖片被換成了淘寶的購物二維碼，且這個二維碼格式與原圖的格式不符合，因此成為了一張“損壞”圖片。每次訓練遇到這個圖片的時候就會產生NaN。
良好的習慣是，你有一個檢測性的網路，每次訓練目標網路之前把所有的樣本在這個檢測性的網路裡面過一遍，去掉非法值。

4、池化層中步長比核的尺寸大

如下例所示，當池化層中stride > kernel的時候會在y中產生NaN

    layer {
      name: "faulty_pooling"
      type: "Pooling"
      bottom: "x"
      top: "y"
      pooling_param {
      pool: AVE
      stride: 5
      kernel: 3
      }
    }

.
.

三、一些訓練時候出現的問題

本節轉載於公眾號深度學習大講堂，文章《caffe程式碼夜話1》

1、為啥label需要從0開始？

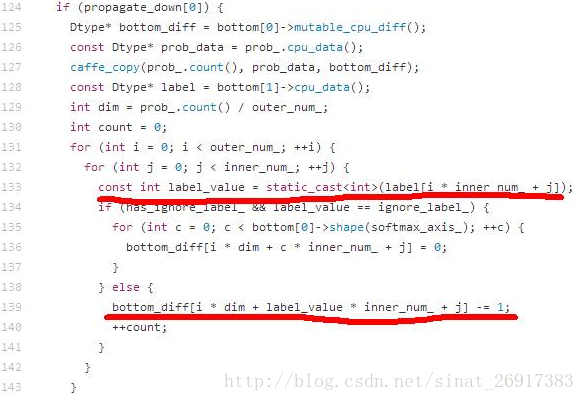
在使用SoftmaxLoss層作為損失函式層的單標籤分類問題中，label要求從零開始，例如1000類的ImageNet分類任務，label的範圍是0~999。這個限制來自於Caffe的一個實現機制，label會直接作為陣列的下標使用，具體程式碼SoftmaxLoss.cpp中133行和139行的實現程式碼。

132行第一層for迴圈中的outer_num等於batch size，對於人臉識別和影象分類等單標籤分類任務而言，inner_num等於1。如果label從1開始，會導致bottom_diff陣列訪問越界。
.

2、為什麼Caffe中引入了這個inner_num，inner_num等於什麼

從FCN全卷積網路的方向去思考。FCN中label標籤長度=圖片尺寸
caffe引入inner_num使得輸入image的size可以是任意大小，innuer_num大小即為softmax層輸入的height*width
.

3、在標籤正確的前提下，如果倒數第一個全連線層num_output > 實際的類別數，Caffe的訓練是否會報錯？

不會報錯且無影響
.

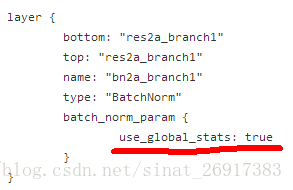
4、BN中的use_global_status

圖2. ResNet部署階模型Proto檔案片段

但是如果直接拿這個Proto用於訓練（基於隨機初始化），則會導致模型不收斂，原因在於在Caffe的batch_norm_layer.cpp實現中，use_global_stats==true時會強制使用模型中儲存的BatchNorm層均值與方差引數，而非基於當前batch內計算均值和方差。

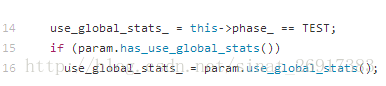
首先看use_global_stats變數是如何計算的：

圖3. use_global_stats計算

再看這個變數的作用：

圖4. use_global_stats為true時的行為

以下程式碼在use_global_stats為false的時候通過moving average策略計算模型中最終儲存的均值和方差：

圖5. BatchNorm層均值和方差的moving average

因此，對於隨機初始化訓練BatchNorm層，只需要在Proto檔案中移除use_global_stats引數即可，Caffe會根據當前的Phase(TRAIN或者TEST)自動去設定use_global_stats的值。
.

5、BatchNorm層是否支援in place運算，為什麼？

BN是對輸入那一層做歸一化操作，要對每個元素-均值/標準差，且輸入輸出規格相當，是可以進行in place。
標準的ReLU函式為max(x, 0)，而一般為當x > 0時輸出x，但x <= 0時輸出negative_slope。RELU層支援in-place計算，這意味著bottom的輸出和輸入相同以避免記憶體的消耗。
.
.

四、過擬合解決：dropout、batch Normalization

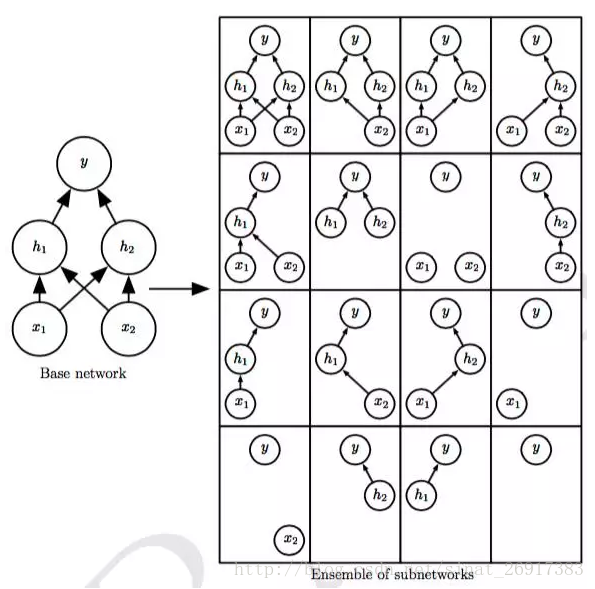
1、dropout——另類Bagging（類似隨機森林RF）

引用自Dropout作者：
在標準神經網路中，每個引數接收的導數表明其應該如何變化才能使最終損失函式降低，並給定所有其它神經網路單元的狀態。因此神經單元可能以一種可以修正其它神經網路單元的錯誤的方式進行改變。而這就可能導致複雜的共適應(co-adaptations)。由於這些共適應現象沒有推廣到未見的資料，將導致過擬合。我們假設對每個隱藏層的神經網路單元，Dropout通過使其它隱藏層神經網路單元不可靠從而阻止了共適應的發生。因此，一個隱藏層神經元不能依賴其它特定神經元去糾正其錯誤。（來源：賽爾譯文 Dropout分析）

Dropout可以被認為是整合非常多的大神經 網路的實用Bagging方法。當每個模型是一個大型神經網路時,這似乎是不切實際的,因為訓練和 評估這樣的網路需要花費很多執行時間和記憶體。
Dropout提供了一種廉價的Bagging整合近似,能夠訓練和評估指數級的神經網路。
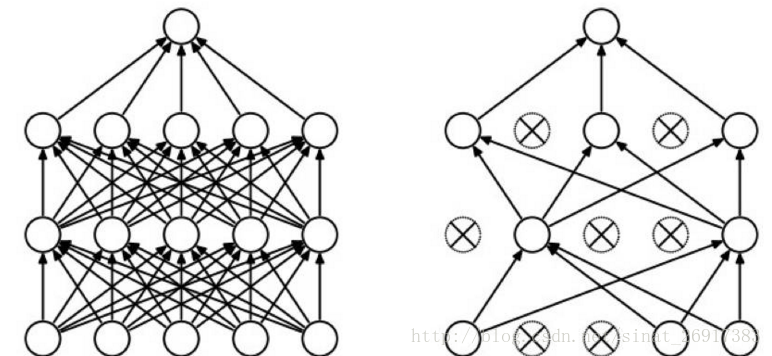
操作方法：將一些單元的輸出乘零就能有效地刪除一個單元。

（1）具體工作過程：

Dropout以概率p關閉神經元，相應的，以大小為q=1-p的概率開啟其他神經元。每個單個神經元有同等概率被關閉。當一個神經元被丟棄時，無論其輸入及相關的學習引數是多少，其輸出都會被置為0。
丟棄的神經元在訓練階段的前向傳播和後向傳播階段都不起作用：因為這個原因，每當一個單一的神經元被丟棄時，訓練階段就好像是在一個新的神經網路上完成。
訓練階段，可以使用伯努利隨機變數、二項式隨機變數來對一組神經元上的Dropout進行建模。
（來源：賽爾譯文 Dropout分析）

（2）dropout型別：
正向dropout、反向dropout。
反向Dropout有助於只定義一次模型並且只改變了一個引數（保持/丟棄概率）以使用同一模型進行訓練和測試。相反，直接Dropout，迫使你在測試階段修改網路。因為如果你不乘以比例因子q，神經網路的輸出將產生更高的相對於連續神經元所期望的值（因此神經元可能飽和）：這就是為什麼反向Dropout是更加常見的實現方式。

（3）dropout與其他規則

故反向Dropout應該與限制引數值的其他歸一化技術一起使用，以便簡化學習速率選擇過程

正向Dropout：通常與L2正則化和其它引數約束技術（如Max Norm1）一起使用。正則化有助於保持模型引數值在可控範圍內增長。
反向Dropout：學習速率被縮放至q的因子，我們將其稱q為推動因子（boosting factor），因為它推動了學習速率。此外，我們將r(q)稱為有效學習速率(effective learning rate)。總之，有效學習速率相對於所選擇的學習速率更高：由於這個原因，限制引數值的正則化可以幫助簡化學習速率選擇過程。
（來源：賽爾譯文 Dropout分析）

（4）優勢：

• 看作是對輸入內容的資訊高度智慧化、自適應破壞的一種形式,而不是 對輸入原始值的破壞。

• Dropout不僅僅是訓練一個Bagging的整合模型,並且是共享隱藏單元的整合模型。這意味著無論其他隱藏單元是否在模型中,每個隱藏單元必須都能夠表現良好。隱藏單元必須準備好進行模型之間的交換和互換。

• 計算方便是Dropout的一個優點。訓練過程中使用Dropout產生 n 個隨機二進位制 數與狀態相乘,每個樣本每次更新只需 O(n)的計算複雜度。

• Dropout的另一個顯著優點是不怎麼限制適用的模型或訓練過程。幾乎在所有 使用分散式表示且可以用隨機梯度下降訓練的模型上都表現很好。包括前饋神經網 絡、概率模型,如受限玻爾茲曼機(Srivastava et al., 2014),以及迴圈神經網路(Bayer and Osendorfer, 2014; Pascanu et al., 2014a)。許多其他差不多強大正則化策略對模 型結構的限制更嚴格。

（5）劣勢：

• Dropout是一個正則化技術,它減少了模型的有效容量。為了抵消這種影響,我們必須增大模型規模。不出意外的話,使 用Dropout時最佳驗證集的誤差會低很多,但這是以更大的模型和更多訓練演算法的迭
  代次數為代價換來的。對於非常大的資料集,正則化帶來的泛化誤差減少得很小。在
  這些情況下,使用Dropout和更大模型的計算代價可能超過正則化帶來的好處。

• 只有極少的訓練樣本可用時,Dropout不會很有效。在只有不到 5000 的樣本 的Alternative Splicing資料集上 (Xiong et al., 2011),貝葉斯神經網路 (Neal, 1996)比Dropout表現更好
  (Srivastava et al., 2014)。當有其他未分類的資料可用時,無監 督特徵學習比Dropout更有優勢。
  .

2、batch Normalization

batch normalization的主要目的是改善優化,但噪音具有正則化的效果,有時使Dropout變得沒有必要。
引數訓練過程中多層之間協調更新的問題：在其他層不改變的假設下,梯度用於如何更新每一個引數。但是，一般情況下會同時更新所有層。 這造成了很難選擇一個合適的學習速率,因為某一層中引數更新的效果很大程度上取決 於其他所有層。
batch normalization可應用於網路 的任何輸入層或隱藏層。設 H 是需要標準化的某層的minibatch激勵函式,佈置為 設計矩陣,每個樣本的激勵出現在矩陣的每一行中。標準化 H,我們替代它為

其中 μ 是包含每個單元均值的向量,σ 是包含每個單元標準差的向量。
反向傳播這些操作,計算均值和標準差,並應用它們於標準化 H。這意味著,梯度不會再簡單地增加 hi 的標準差或均值;標準化操作會 除掉這一操作的影響,歸零其在梯度中的元素。

以前的方法新增代價函式的懲罰,以鼓勵單位標準化激勵統計量,或是 在每個梯度下降步驟之後重新標準化單位統計量。
前者通常會導致不完全的標準化, 而後者通常會顯著地消耗時間,因為學習演算法會反覆改變均值和方差而標準化步驟 會反覆抵消這種變化。
batch normalization重新引數化模型,以使一些單元總是被定 義標準化,巧妙地迴避了這兩個問題。