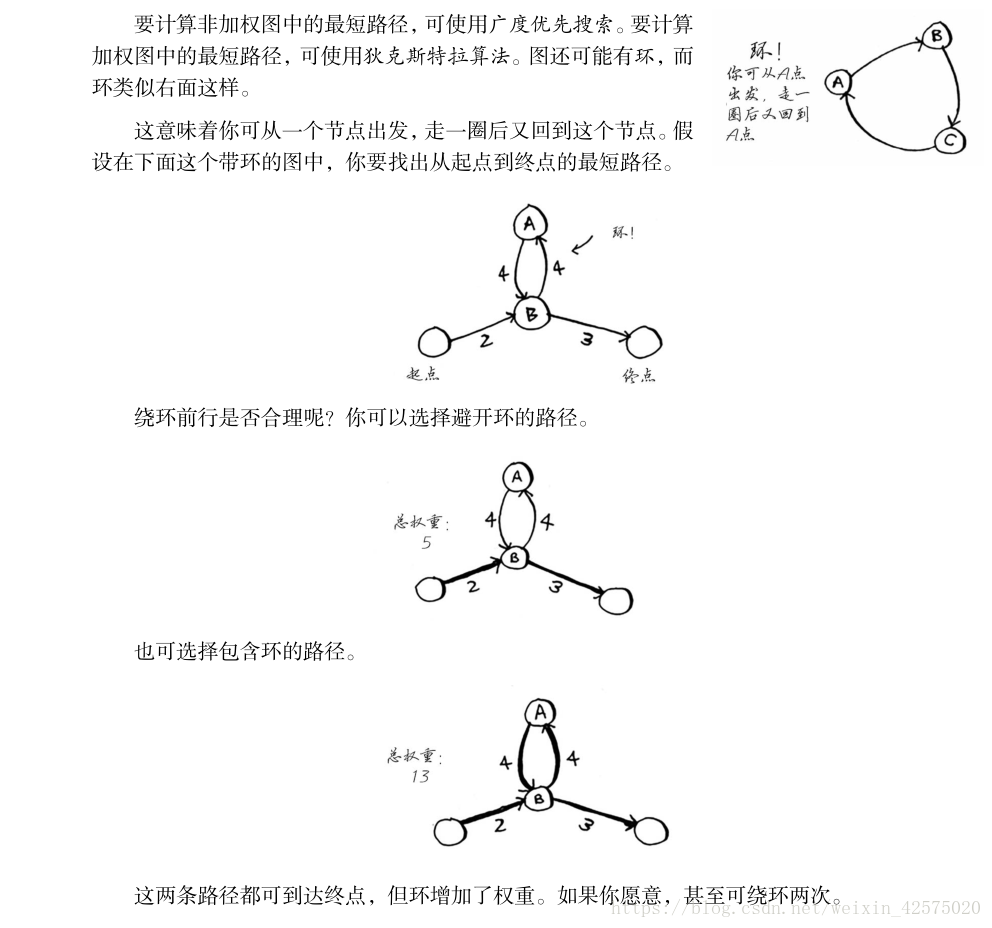
狄克斯特拉演算法找最短路徑問題:

之前我們瞭解過，用廣度優先搜尋，找出段數最少的路徑，但是要找出最快的路徑該怎麼做呢，為此我們可以用現在提到的演算法，狄克斯特拉演算法。

我們知道，狄克斯特拉算的輔助圖形必須是有向無環加權圖，這也就決定了該演算法的使用條件。

那什麼是有向無環加權圖呢？下面舉個例子說明一下

另外，值得注意的是：狄克斯特拉演算法同樣不適用於含有負權邊的圖，即是，圖上的數字不能為負值。

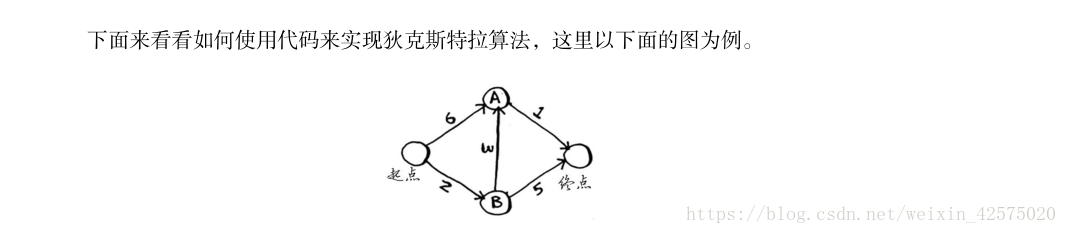
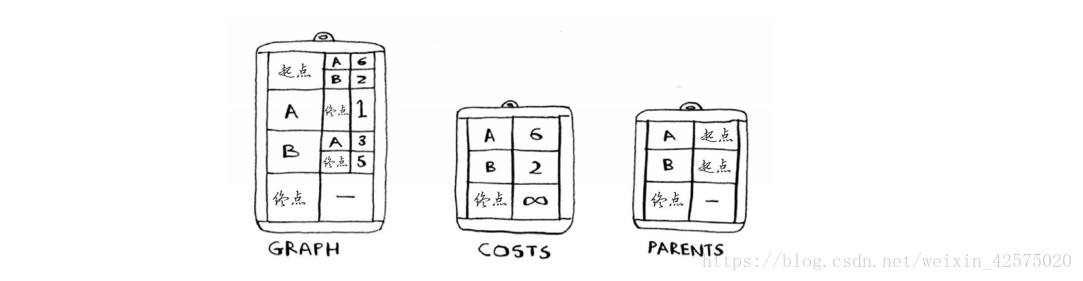
要實現演算法需要一下準備工作，首先需要三個散列表，就是python的字典。

然後我們來看一下程式碼流程

接下來直接上程式碼：

def find_lowest_cost_node(costs):
    lowest_cost = float("inf")
    lowest_cost_node = None
    for node in costs:   <---------遍歷所有的節點
        cost = costs[node]
        if cost < lowest_cost and node not in processed: <----如果當前節點的開銷更低且未處理過
            lowest_cost = cost  <--------將其視為開銷最低的節點
            lowest_cost_node = node
    return lowest_cost_node

這是找出獲取花費最低節點的函式

node = find_lowest_cost_node(costs) <------在未處理的節點中找出開銷最小的節點
while node is not None:  <-----這個while迴圈在所有節點都被處理過後結束
    cost = costs[node]
    neighbors = graph[node]
    for n in neighbors.keys():  <---遍歷當前節點的所有鄰居
        new_cost = cost + neighbors[n]
        if costs[n] > new_cost: <------如果經當前節點前往該鄰居更近，
            costs[n] = new_cost  <----就更新該鄰居的開銷
            parents[n] = node  <-----同時將該鄰居的父節點設定為當前節點
    processed.append(node)  <------將當前節點標記為處理過
    node = find_lowest_cost_node(costs) <---找出接下來要處理的節點，並迴圈