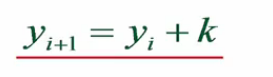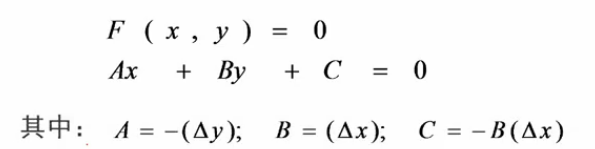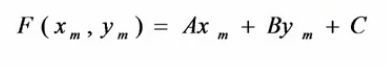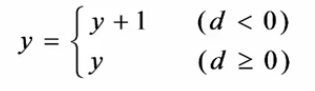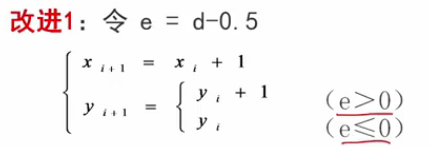計算機圖形學 學習筆記(一):概述,直線掃描轉換演算法:DDA,中點畫線演算法,Bresenham演算法
前言
感謝中國農大 趙明老師的分享~
現在我要為我自己走向遊戲程式設計打下基石~
1 計算機圖形學概論
1.1 計算機圖形學課程簡介
《計算機圖形學》是計算機、地理資訊系統、應用數學、機械、建築等專業本科教學中的一門重要的專業基礎課
如影象處理、模式識別、多媒體技術、計算機視覺等的基礎
在CAD/CAM、計算機動畫、系統環境模擬、地理資訊系統、計算機藝術、真實感圖形顯示、科學計算的視覺化、3D列印的等領域都有重要的應用
該門課程使學生了解計算機圖形學的發展、掌握圖形學的基本原理、演算法和實現技術。學會基本的圖形軟體開發技術,為進一步學習後續課程打下良好的基礎。
參考書籍:
- 《計算機圖形學基礎課程》 孫家廣、胡事民,清華出版社
- 《計算機圖形學(OpenGL版)(第3版)》胡事民,劉永進等 清華大學出版社
- 《計算機圖形學基礎》 陸楓、何雲峰 電子出版社
- 《計算機輔助設計與圖形學學報》
- 《中國影象圖形學報》
1.2 計算機圖形學概述
計算機圖形學定義
簡單來說,計算機圖形是計算機產生的影象。
定義:計算機圖形學就是研究如何在計算機中表示圖形、以及利用計算機進行圖形的計算、處理和顯示的相關原理與演算法
計算機圖形學研究內容
如何在計算機中表示圖形、以及利用計算機進行圖形的計算、處理和顯示的相關原理與演算法,構成了計算機圖形學的主要研究內容。
圖形硬體:研究圖形要有基本的支撐硬體,包括圖形加速卡、顯示器、圖形輸出裝置等等。
一般來說,要在計算機上生成一副表示物體的圖形,有三個步驟
造型技術
在計算機中建立索要生成影象的物體的模型,即給出表示該物體的集合資料和拓撲關係。光照模型
自然光照現象是由一些物理學定律所決定的,而這些物理學定律又非常複雜
所以,希望用一些簡單的數學模型來近似、代替那些物理學的模型,為模擬物體表面的光照物理現象的數學模型叫光照模型繪製(渲染)技術
第三步是選擇適當的繪製演算法來把這個場景畫(渲染)出來。就是將模型真實性顯示在螢幕上。
渲染一幅三維物體影象所涉及的知識、實際上就是計算機圖形中每個畫素看上去應該是什麼顏色的問題。這很大程度上取決於不同的光照模型。
計算機螢幕是由畫素構成的,畫素作為構成圖形的基本單位。為了在螢幕上顯示一幅圖形,就必須研究在哪些畫素上生成圖形,就必須有一套針對光柵顯示器生成圖形的演算法。
計算機圖形學發展歷史
要了解一門學科的發展,最好的就是了解它的發展歷史
(百度去吧少年們)
計算機圖形學的應用領域
- 人機互動和圖形使用者介面
- 計算機輔助設計與製造(CAD/CAM)
- 真實感圖形繪製與自然景物方針
- 計算機遊戲、電影、動漫
- 計算機藝術
- 計算機方針
- 科學計算視覺化
- 虛擬現實
- 地理資訊系統(GIS)
- 農業領域的應用
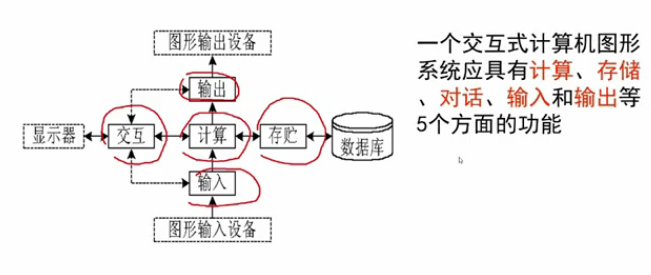
計算機圖形處理系統組成
2 光柵圖形學演算法
隨著光柵顯示器的出現,為了在計算機上處理、顯示圖形,需要發展一套與之相適應的演算法:光柵圖形學演算法。
光柵圖形演算法多數屬於計算機圖形的底層演算法,很多圖形學的基本概念和思想都在這一章。
光柵圖形學演算法的研究內容
- 直線段的掃描轉換演算法
- 多邊形的掃描轉換與區域填充演算法
- 裁剪演算法
- 反走樣演算法
- 消隱演算法
2.1 直線段的掃描轉換演算法—DDA
在數學上,直線上的點有無窮多個。但當在計算機光柵顯示器螢幕上表示這條直線時需要做一些處理(因為光柵顯示器是由一個個畫素點構成的,而畫素又是有限的)
為了在光柵顯示器上用有限的點逼近無限的點構成的直線,需要知道這些畫素點的x,y座標
DDA畫線演算法 1
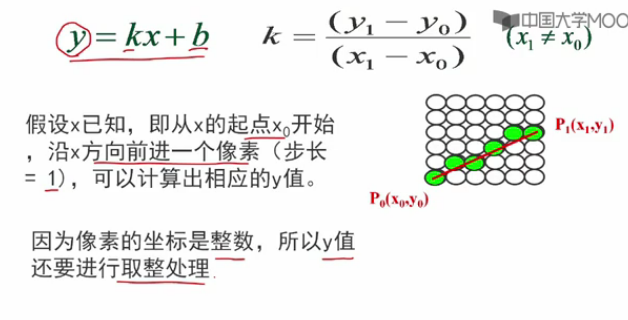
如何把數學上的一個點掃描轉換成一個頻幕畫素點?(因為畫素點都是整數,所以我要對點進行取整處理,x和y都要是整數)
y=kx+b
直線是最基本的圖形,一個動畫或真實感圖形往往需要呼叫成千上萬次畫執行緒序,因此直線演算法的好壞與效率將直接影響圖形的質量和顯示速度。
回顧一下剛才的演算法:
y=kx+b(直線斜截式方程)
這個演算法,有乘法運算和加法運算,還有後期的取整運算。
為了提高效率,把計算量減下來,關鍵問題就是如何把乘法取消?(因為計算機中加減乘除,加法的運算效率最快)
DDA畫線演算法 2
為了提高效率,把乘法取消。我們需要學習三個著名的常用演算法。
直線繪製的三個著名的常用演算法
- 數值微分法(DDA)
- 中點畫線法
- Bresenham演算法
一、數值微分法DDA
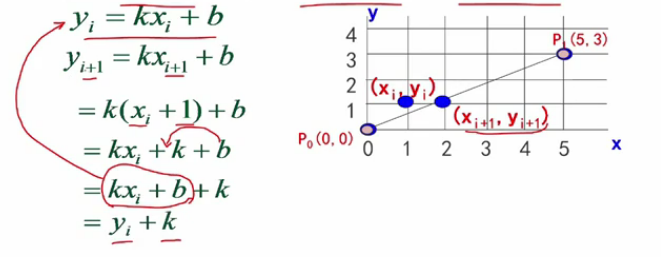
引進圖形學中一個很重要的思想—增量思想。
注:之所以能寫成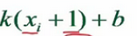
這樣也就是說
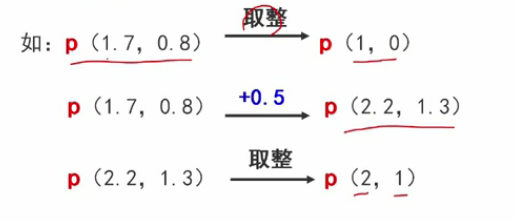
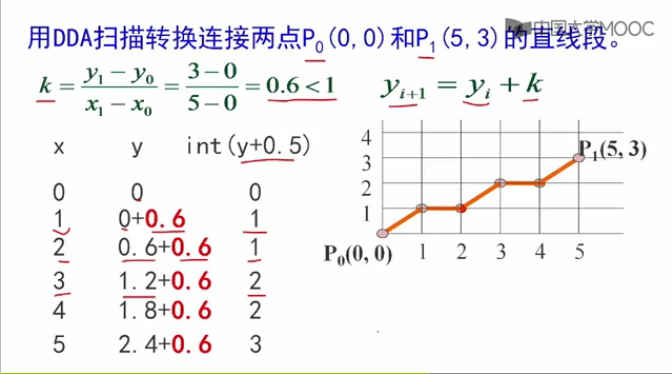
例子:
【思考題】
DDA畫直線演算法:x每遞增1,y遞增斜率k。是否適合任意斜率的直線?
(1) | k | <= 1 時,
(2) | k | > 1 時,
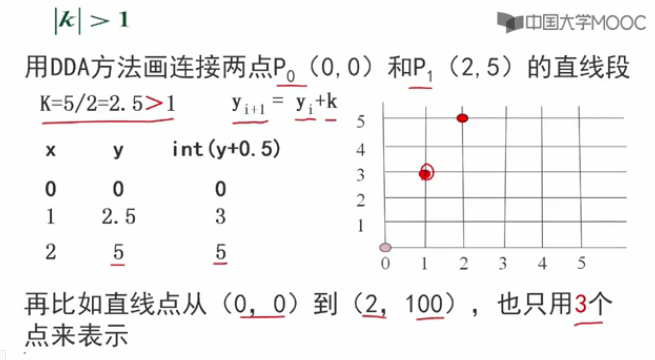
如果K>1,會導致光柵點太稀了!
除開起點和終點,中間只有1個點,而1個點完全無法表達直線的趨勢。
那麼如何解決K>1時的直線掃描演算法呢?
2.2 直線段的掃描轉換演算法—中點畫線
採用增量思想的DDA演算法,直觀、易實現,每計算一個畫素座標,只需計算一個加法。
這個演算法是否最優呢?若非最優,如何改進?
(我們在2.1中已經知道DDA不適合於斜率k>1的情況)
(1)改進效率
這個演算法每步只做一個加法,能否再提高效率呢?
計算機執行最快的就是加法。
但是加法分為整數加法和浮點加法。
一般情況下k與k都是小數,而且每一步運算都要對y進行四捨五入後取整。
唯一改進的途徑就是把浮點運算變成整數加法。
(2)改善直線方程型別
這樣就引出了中點畫線演算法~~~
中點畫線演算法 1
直線的一般式方程:
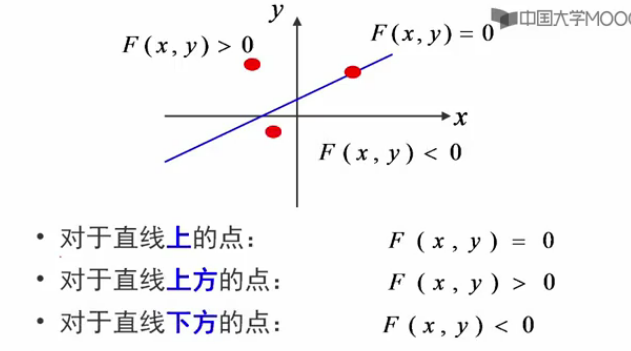
這個方程把螢幕分成3部分
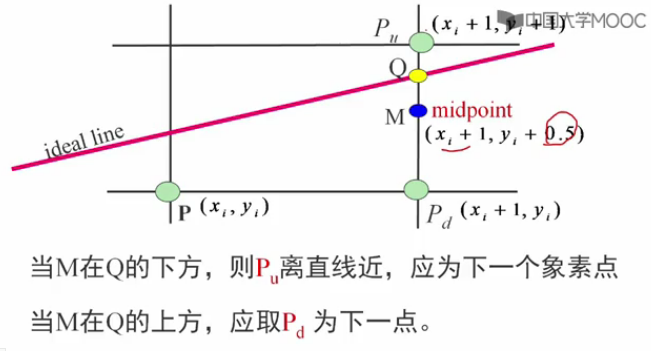
思想:每次在最大位移方向(最大位移發現就是+1,到達螢幕的另一部分)上走一步,而另一個方向是走還是不走要取決於中點誤差項的判斷(兩個方向就x和y)。
假定:0<=| k |<=1。因此,每次在x方向上加1,y方向上加1或不變需要判斷。
如何判斷Q在M的上方還是下方呢?
把M的座標代入理想直線方程:
假如M的座標為d(i)
下面來分析一箇中點畫線演算法的計算量
雖然中點畫線演算法解決了斜率大於1時,DDA演算法不精確的問題。
但明顯的是這個計算量就比DDA大多了(DDA是1個乘法1個加法)
那麼能否也採用增量計算,提高計算效率呢?
中點畫線演算法 2
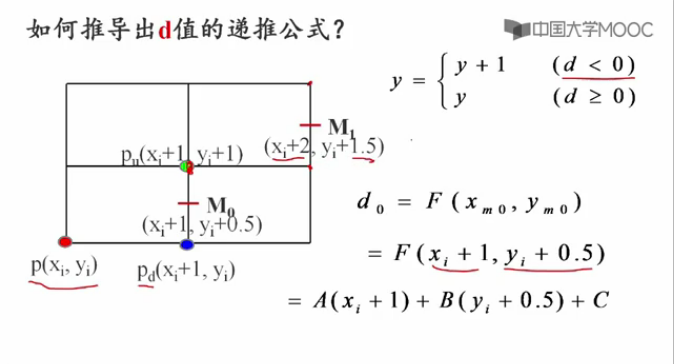
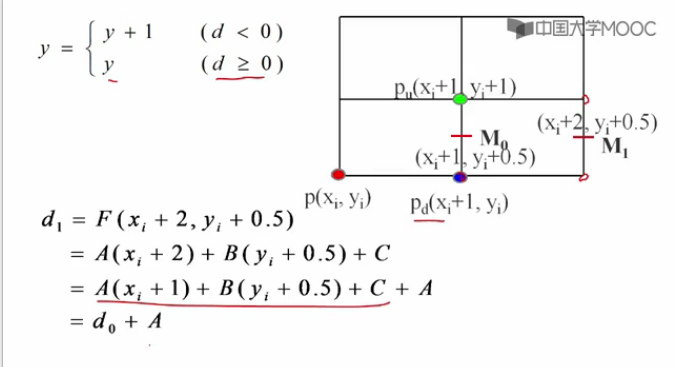
如何推匯出d值得遞推公式?
(1)d<0 的情況下
(2)d>0 的情況下
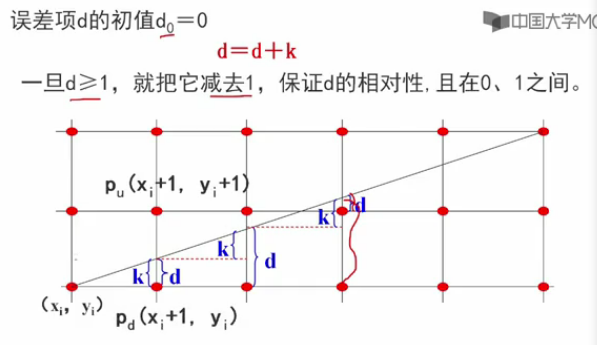
下面計算d的初始值d[0]
完整的中點畫線演算法
【小結】
- 中點畫線演算法採用直線一般式方程,而DDA採用斜截式方程
- 通過判斷中點額符號,最終可以只進行整數加法
這個演算法是否還有改進的餘地?
2.3 直線段的掃描轉換演算法—Bresenham演算法
中點畫線法
這個演算法是否還有改進的餘地?
從計算機的運算效率來說。中點畫線只做一個整數加法,而整數加法已經是最快的了。
那麼只能從直線的方程入手。
能否提出一個演算法,使這個演算法不但能解決畫直線,還能解決圓弧、拋物線甚至自由曲線的光柵化問題,使演算法的覆蓋域擴大。
這就引出了Bresenham演算法。
Bresenham演算法 1
DDA把演算法效率提高到每步只做一個加法。(加法中間有乘法運算)
中點演算法進一步把效率提高到每步只做一個整數加法。
Bresenham演算法提供了一個更一般的演算法。該演算法不僅有好的效率,而且有更廣泛的適用範圍。
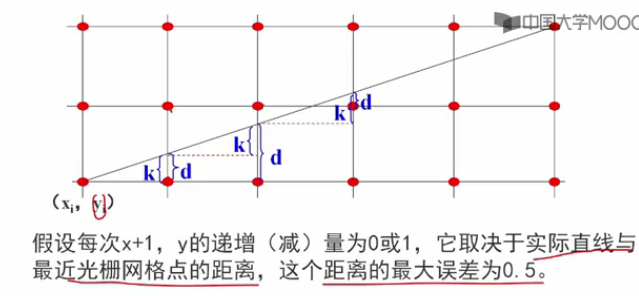
Bresenham演算法的基本思想
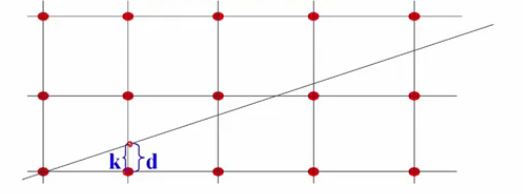
該演算法的思想是通過各行、各列畫素中心構造一組虛擬網路線,按照直線起點到終點的順序,計算直線與各垂直網格線的交點,然後根據誤差項的符號確定該列畫素中與此交點最近的畫素。
Bresenham演算法 2
(1)改進e
(2)改進 e初 和 k
演算法步驟為:
Bresenham演算法很像DDA演算法,都是加斜率。
但DDA演算法使判斷符號來決定上下兩個點。所以該演算法集中DDA和終點兩個演算法的優點,而且應用範圍廣泛。
【小結】
- 電腦科學問題的核心就是演算法
- 領會演算法中所蘊含的創新思想
- 科學研究無止境,學術面前人人平等