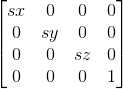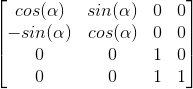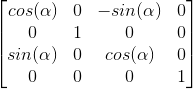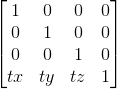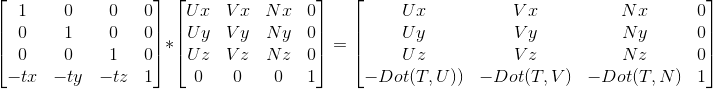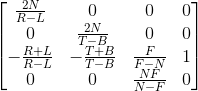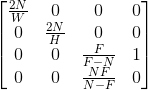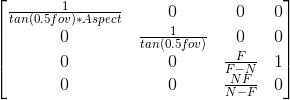簡介

這是可能一篇沒有什麼實際作用的文章，因為沒有任何shader效果實現，整篇文章到最後，我只實現了一個旋轉的立方體（o(╯□╰)o，好弱），和遊戲引擎渲染的萬紫千紅的3D世界顯得有很大落差，彷彿一切都回到了最初的起點（不知道有沒有人能猜出來左側的是哪部遊戲大作的截圖(*^▽^*)）。

不過實時渲染繁華的背後，還是這看似簡單的光柵化。今天，本人打算學習一下基本的光柵化渲染的過程，看一下怎樣把一個模型從一些頂點資料，變成最終顯示在螢幕上的影象，也就是所謂的渲染流水線。

所謂SoftRenderer（軟渲染），就是用純程式碼邏輯模擬OpenGL或者D3D渲染流水線，當然，只是實現了冰山一角，軟渲染沒有什麼實際運用意義，但是對學習渲染原理來說應該是一個比較有效的手段了。之前開了個SoftRenderer的小坑，只是實現了基本的3D變換，三角形圖元繪製，仿射紋理對映，最近本想寫一篇深度相關的blog的，奈何寫了一半發現好多內容需要推導計算，於是乎索性先把軟渲染的坑補完，正好這幾天把透視校正紋理對映加上了，順便修了幾個bug，基本可以執行起來了（然而我只畫了個正方體，幀率還慘不忍睹）。一些高階的特性，比如法線貼圖，複雜光照，雙線性取樣，RT之類的就等之後再慢慢填坑啦（恩，這很有可能是個棄坑-_-）。

簡單介紹一下，專案使用的是C++，類似D3D的3D模式，左手座標系，NDC中Z是（0,1）區間，向量為行向量，左乘矩陣，沒有第三方庫，只用到了Windows GDI相關，工程VS2015。基本實現了模型->世界->齊次裁剪空間->裁剪->透視除法->視口對映->ZBuffer深度測試->透視校正紋理對映等功能。實現過程中參考了知乎大佬們的各種回答。本人才疏學淺，尤其是渲染這裡，很可能只是“看起來是對的“，再加上哥們600多的近視，所以如果有錯誤，還望各位高手批評指正。

渲染流水線

《Real Time Renderering》中把渲染流水線的功能簡要描述如下：給定一個虛擬相機，一些三維物體，燈光，著色方程，貼圖等資源，最終生成一張二維圖片的過程。所謂流水線Pipline，也就是把原本線性執行的工作，改為並行執行，這樣可以極大地提高效率。流水線的瓶頸也就是流水線中最弱的（耗時最長的）。渲染流水線在《RTR》中定義為三個基本階段，而每一個階段裡面，又分為一些具體的操作步驟，下面分別看一下。

Application（應用程式階段）：字面意思即可，就是相對於渲染來說，其他的內容基本都可以定義在這個階段。比如遊戲邏輯，物理等等。個人理解為在呼叫DrawCall之前的階段，該階段主要在CPU上進行。

Geometry（幾何階段）：主要是頂點著色器（MVP變換），裁剪，螢幕對映。處理上一階段傳遞進來的圖元和位置等資訊，計算變換位置，最終決定物體在螢幕上的哪個位置，過程中還需進行裁剪，計算一些需要傳遞給下一階段的資料。下圖是《RTR3》中定義的Gemmetry階段：

Rasterizer（光柵化階段）：光柵化階段是將上一階段變換投影對映後螢幕空間的頂點（包括頂點包含的各種資料），轉化為螢幕上畫素的一個過程。在該階段主要進行的是三角形資料的設定，資料插值，畫素著色（包括紋理取樣），Alpha測試，深度測試，模板測試，混合。

為了更好地顯示，一般會採用雙緩衝技術，即在backbuffer渲染，完成後swap到前臺。

上面的流水線，可能並不是很全面，新版本的有可能有Geometry Shader，Early-Z，Tiled Based等等，而且這個東西每個廠商可能都不太一樣，但是上面的應該算是比較經典的一個流水線，並且都是必不可少的階段（曾經以為裁剪可以不用，偷一點懶，大不了效能差點，後來發現自己真是太天真）。

下面本人就來大致實現基本的渲染流水線，本文的順序是繪製直線，三角形，MVP矩陣變換，裁剪，視口對映，深度測試，透視校正紋理取樣，是以複雜度作為順序，並非真正的渲染順序。

繪製直線

首先來研究一下怎麼繪製直線，軟渲染中每一個階段其實都有多種方法進行實現，只不過有些是比較公認的通用方案。我這裡只是找了一個適合我的方案。

我們顯示在螢幕上的影象，其實就是一幅二維圖片，而圖片其實是離散的，換句話說，就是一個二維陣列，螢幕的座標就是陣列的索引。所以，實際上我們在光柵化階段繪製的時候，直接使用int型資料即可。俗話說得好，兩點確定一條直線，那麼，這一個步驟的輸入就是兩個二維座標，輸出就是一條直線。

實現畫線有幾種演算法，DDA（最易理解，直接算斜率，有除法，不利於硬體實現，慢），Bresenham演算法（沒有除法和浮點數，快），吳小林演算法（帶抗鋸齒，比Bresenham慢）。這裡，我採用了Bresenham演算法進行繪製：

//斜率k = dy / dx
//以斜率小於1為例，x軸方向每單位都應該繪製一個畫素，x累加即可，而y需要判斷。
//誤差項errorValue = errorValue + k，一旦k > 1，errorValue = errorValue - 1，保證0 < errorValue < 1
//errorValue > 0.5時，距離y + 1點較近，因而y++，否則y不變。
int dx = x1 - x0;
int dy = y1 - y0;
float errorValue = 0;
for (int x = x0, y = y0; x <= x1; x++)
{
	DrawPixel(x, y);
	errorValue += (float)dy / dx;
	if (errorValue > 0.5)
	{
		errorValue = errorValue - 1;
		y++;
	}
}

上面演算法的主要思想是，按照直線的一個方向，以斜率小於1為例的話，在x軸方向每次步進一個畫素，y判斷離哪個畫素近。通過y方向增加一個累計誤差值，當誤差值超過1了，說明y方向應該上移一個畫素，否則仍然是距離當前y值近。不過上面的演算法還是沒有避免掉除法的問題，我們可以通過修改一下判斷的條件，去掉除法和浮點數，並完善各種情況：

void ApcDevice::DrawLine(int x0, int y0, int x1, int y1)
{
	int dx = x1 - x0;
	int dy = y1 - y0;

	int stepx = 1;
	int stepy = 1;
	
	if (dx < 0)
	{
		stepx = -1;
		dx = -dx;
	}

	if (dy < 0)
	{
		stepy = -1;
		dy = -dy;
	}

	int dy2 = dy << 1;
	int dx2 = dx << 1;

	int x = x0;
	int y = y0;
	int errorValue;

	//改為整數計算，去掉除法
	if (dy < dx)
	{
		errorValue = dy2 - dx;
		for (int i = 0; i <= dx; i++)
		{
			DrawPixel(x, y);
			x += stepx;
			errorValue += dy2;
			if (errorValue >= 0)
			{
				errorValue -= dx2;
				y += stepy;
			}
		}
	}
	else
	{
		errorValue = dx2 - dy;
		for (int i = 0; i <= dy; i++)
		{
			DrawPixel(x, y);
			y += stepy;
			errorValue += dx2;
			if (errorValue >= 0)
			{
				errorValue -= dy2;
				x += stepx;
			}
		}
	}
}

那麼，我們隨機在螢幕上畫兩條線的效果如下，解析度是600*450，仔細看鋸齒還是挺嚴重的，也讓我深刻地意識到了抗鋸齒的重要性o(╯□╰)o：

繪製三角形

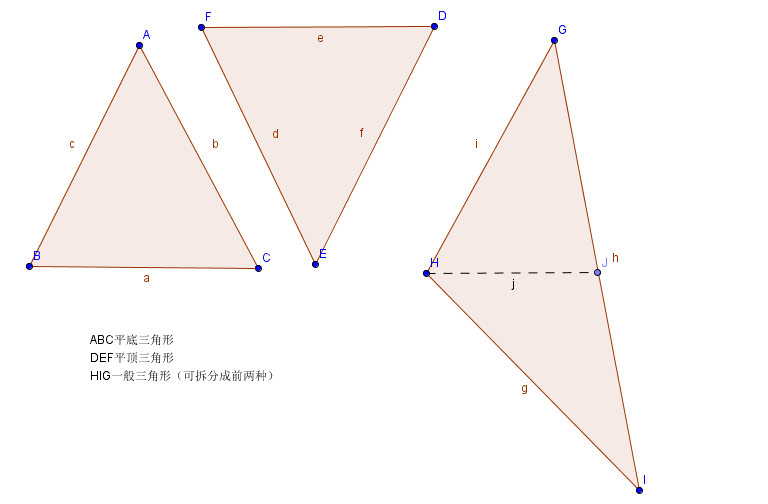
邁出了最難的第一步，接下來就會好很多了。點，線，面，三個點確定一個三角形，所以我們再加一個引數，繪製一個三角形看一下。但是此處並非直接給三個點，連在一起，而是要把三角形內部填充上顏色。最簡單的填充就是掃描線填充，換句話說我們按照螢幕的y軸方向，從上向下，每一行進行繪製，直到把三角形全部填充上為止。首先要把三角形分一下類：

我們已知的是y的方向，那麼就需要帶入三角形邊的直線方程求得x的座標，然後在兩個點之間畫線。如果三角形是平頂的或者是平底的，那麼我們只需要考慮兩條邊即可，但是如果是一般的三角形，我們就需要做一下拆分，把三角形劃分成一個平頂三角形和一個平底三角形，以上圖為例，三角形GHI，以H的y值帶入GI直線方程求得J的x座標，生成GHJ和HJI兩個三角形，這兩個三角形就可以按照平頂和平底的方式進行光柵化了。

以平底三角形ABC為例，假設A（x0，y0），B（x1，y1），C（x2，y2），AB直線上隨機一點（x，y）,那麼直線方程如下：

（y - y1） / （x - x1） = （y0 - y1） / （x0 - x1），我們已知y（從y0到y1迴圈），則x值為： x = （y - y0） * (x0 - x1) /  (y0 - y1) + x1。AC邊類似得到x值，那麼迴圈中我們就可以根據y值得到每條掃描線左右的x值。平底和平頂三角形的繪製程式碼如下：

void ApcDevice::DrawBottomFlatTrangle(int x0, int y0, int x1, int y1, int x2, int y2)
{
	for (int y = y0; y <= y1; y++)
	{
		int xl = (y - y1) * (x0 - x1) / (y0 - y1) + x1;
		int xr = (y - y2) * (x0 - x2) / (y0 - y2) + x2;
		DrawLine(xl, y, xr, y);
	}
}

void ApcDevice::DrawTopFlatTrangle(int x0, int y0, int x1, int y1, int x2, int y2)
{
	for (int y = y0; y <= y2; y++)
	{
		int xl = (y - y0) * (x2 - x0) / (y2 - y0) + x0;
		int xr = (y - y1) * (x2 - x1) / (y2 - y1) + x1;
		DrawLine(xl, y, xr, y);
	}
}

知道了平頂和平底，我們只要根據拐點計算出拐點y軸對應另一邊的x值，生成新的三角形即可。但是此處我們為了程式碼簡單一些，先對傳入的三個頂點進行一下排序：、

void ApcDevice::DrawTrangle(int x0, int y0, int x1, int y1, int x2, int y2)
{
	//按照y進行排序，使y0 < y1 < y2
	if (y1 < y0)
	{
		std::swap(x0, x1);
		std::swap(y0, y1);
	}
	if (y2 < y0)
	{
		std::swap(x0, x2);
		std::swap(y0, y2);
	}
	if (y2 < y1)
	{
		std::swap(x1, x2);
		std::swap(y1, y2);
	}

	if (y0 == y1)	//平頂三角形
	{
		DrawTopFlatTrangle(x0, y0, x1, y1, x2, y2);
	}
	else if (y1 == y2) //平底三角形
	{
		DrawBottomFlatTrangle(x0, y0, x1, y1, x2, y2);
	}
	else			//拆分為一個平頂三角形和一個平底三角形
	{
		//中心點為直線(x0, y0)，(x2, y2)上取y1的點
		int x3 = (y1 - y0) * (x2 - x0) / (y2 - y0) + x0;
		int y3 = y1;

		//進行x排序，此處約定x2較小
		if (x1 > x3)
		{
			std::swap(x1, x3);
			std::swap(y1, y3);
		}
		DrawBottomFlatTrangle(x0, y0, x1, y1, x3, y3);
		DrawTopFlatTrangle(x1, y1, x3, y3, x2, y2);
	}
}

通過上面的步驟，我們就可以在螢幕上繪製一個填充好的三角形啦，如下圖：

ObjectToWorld矩陣構建

下面就是3D相關的操作了，這也是軟渲染中最有意思的部分。首先就是MVP變換，具體來說就是將模型空間座標通過ObjectToWorld矩陣（M）變換到世界空間，然後通過WorldToView矩陣（V）變換到相機空間，最後通過透視投影矩陣（P）變換到裁剪空間。上述的幾個變換都是由矩陣完成的。關於矩陣，簡單點來說就是一個二維陣列，只是為了更加方便地表達變換的過程，並且這些計算通過矩陣更加容易用硬體進行實現。下面主要用到的是矩陣的乘法，向量與矩陣的乘法，矩陣的轉置等特性。

如果把矩陣的行解釋為座標系的基向量，那麼乘以該矩陣就相當於做了一次座標變換，vM = w，稱之為M將v變換到w。用基向量[1,0,0]與任意矩陣M相乘，得到[m11,m12,m13]，得出的結論是矩陣的每一行都可以解釋為轉化後的基向量。根據該結論，就可以通過一個期望的變換，反向構造出一個矩陣來代表這個變換。首先來看一下MVP的M，也就是模型空間轉世界空間的變換，這個變換也是分為三個子變換，分別是縮放，旋轉，平移。下面分別推導一下幾個變換的矩陣。

縮放矩陣

縮放是最簡單的變換，假設頂點為（x, y, z），縮放係數為（sx, sy, sz），那麼縮放希望的就是（sx *x, sy * y, sz * z），我們用一個矩陣來表示的話就是：

程式碼如下：

Matrix ApcDevice::GenScaleMatrix(const Vector3& v)
{
	Matrix m;
	m.Identity();
	m.value[0][0] = v.x;
	m.value[1][1] = v.y;
	m.value[2][2] = v.z;
	return m;
}

旋轉矩陣

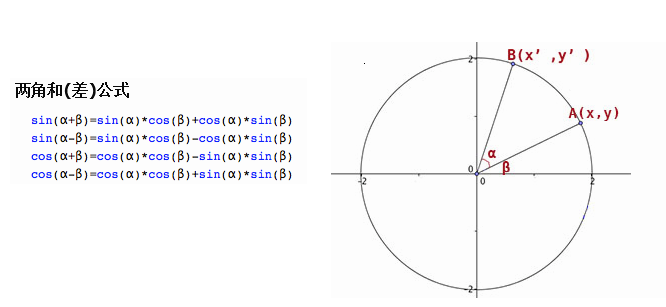
接下來是旋轉矩陣，看起來有點麻煩，而且x，y，z三個方向需要單獨實現，其實又是三個矩陣相乘，這篇文章推導的比較明瞭，借用一張圖：

到這個時候，我才意識到，哇塞，原來三角函式展開的實際應用竟然這麼重要。。。我們要表示一個旋轉，比如繞Z軸旋轉，那麼這個時候，Z軸的座標是不會變化的，所以只考慮X，Y軸座標即可，比如上圖，A為原始座標（x，y），角度為β，旋轉角度α變換到B點（x’,y'），半徑為r。此時，左右手座標系的差別就有了，我使用的是左手座標系，所以用左手拇指指向Z軸正方向（指向螢幕內），另外四指環繞的方向就是旋轉的正方向了。如果用右手座標系，那麼就得換成右手了。

那麼x’= r * cos(α + β) = cos(α) * cos(β) * r - sin(α) * sin(β) * r = cos(α) * x - sin(α) * y

同理y’= r * sin(α + β) = sin(α) * cos(β) * r + cos(α) * sin(β) * r = sin(α) * x + cos(α) * y

根據上面的兩個等式，我們就可以構建出一個矩陣，Z方向不變，置為1即可，矩陣如下：

繞X軸旋轉的矩陣：

繞Y軸旋轉的矩陣：

最終，這樣，每個軸上我們給定一個角度即可得到旋轉的矩陣，最終矩陣為三者相乘，繞三個軸旋轉值按一個Vector傳遞進來：

Matrix ApcDevice::GenRotationMatrix(const Vector3& rotAngle)
{
	Matrix rotX = GenRotationXMatrix(rotAngle.x);
	Matrix rotY = GenRotationYMatrix(rotAngle.y);
	Matrix rotZ = GenRotationZMatrix(rotAngle.z);
	return rotX * rotY * rotZ;
}

Matrix ApcDevice::GenRotationXMatrix(float angle)
{
	Matrix m;
	m.Identity();
	float cosValue = cos(angle);
	float sinValue = sin(angle);
	m.value[1][1] = cosValue;
	m.value[1][2] = sinValue;
	m.value[2][1] = -sinValue;
	m.value[2][2] = cosValue;
	return m;
}

Matrix ApcDevice::GenRotationYMatrix(float angle)
{
	Matrix m;
	m.Identity();
	float cosValue = cos(angle);
	float sinValue = sin(angle);
	m.value[0][0] = cosValue;
	m.value[0][2] = -sinValue;
	m.value[2][0] = sinValue;
	m.value[2][2] = cosValue;
	return m;
}

Matrix ApcDevice::GenRotationZMatrix(float angle)
{
	Matrix m;
	m.Identity();
	float cosValue = cos(angle);
	float sinValue = sin(angle);
	m.value[0][0] = cosValue;
	m.value[0][1] = sinValue;
	m.value[1][0] = -sinValue;
	m.value[1][1] = cosValue;
	return m;
}

上面，我們只考慮物體繞自身軸旋轉，如果需要繞任意一點旋轉的話，我們就可以先進行平移，平移到該點，然後再旋轉，旋轉後再平移回去。即v = vTRT^-1

平移矩陣

原本而言，我們用3x3的矩陣即可表示上面兩種變換，然而平移不行，所以就需要引入一個4x4的矩陣來表達平移變換，比如一個頂點（x，y，z）我們希望它平移（tx，ty，tz）距離，那麼實際上就是（x + tx，y + ty，z + tz）。使用矩陣來表示的話就是：

而如果用4x4矩陣，Vector3顯然也不夠用了，為了能達到上述的變換，我們就需要給Vector增加一個w維度，w = 1時，Vector表示點，與上述矩陣相乘後得到變換的結果，而w = 0時，Vector表示向量，上述變換的結果仍然是Vector自身，平移變換對方向變換不生效。

平移矩陣的程式碼如下：

Matrix ApcDevice::GenTranslateMatrix(const Vector3& v)
{
	Matrix m;
	m.Identity();
	m.value[3][0] = v.x;
	m.value[3][1] = v.y;
	m.value[3][2] = v.z;
	return m;
}

ObjectToWorld矩陣整合

經過上面的步驟，我們得到了縮放矩陣，旋轉矩陣，平移矩陣，最終將三者使用矩陣乘法相乘即可得到完整的ObjectToWorld矩陣，由於我們採用了行向量表示座標，所以相當於左乘，即我們用vSRT的順序進行變換。

我們可以根據矩陣連乘結合律把幾個變換通過矩陣相乘的方法，先計算出一個結果矩陣再用該矩陣去變換頂點，這有一個很大的好處，就是我們可以逐物件計算一次變換整體的變換矩陣，然後這個物件的所有的頂點都應用這個變換。這樣就把變換的時間從n次MVP計算+n次矩陣與頂點相乘變成了1次矩陣MVP計算+n次矩陣與頂點相乘，而且可以避免浮點計算誤差（嘗試了一下逐圖元計算變換矩陣，最後正方形邊界對不上，改為統一計算後效果正常）。我們不需要一些特殊的效果（固定管線），所以我們直接把這個SRT矩陣與後續的VP矩陣相乘，結果再來進行座標的變換。

WorldToCamera矩陣構建 

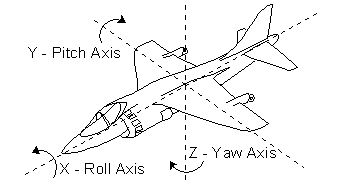
上一階段，我們把頂點從模型空間轉換到了世界空間，但是有一個很重要的問題，相機才是我們觀察世界的視窗，後續的投影，裁剪，深度等如果都在世界空間做的話就太複雜了，如果我們把這些操作的座標原點改為相機，就會大大降低後續操作的複雜性。所以，下一步就是如何將一個世界空間的物件轉化到相機空間。要定義一個相機，首先要有相機位置，還要有相機看的方向，一種方法是給出相機的旋轉角度，也就是Raw,Pitch，Roll這三個值，如下圖：

另一種方案就是給一個相機注視點以及一個控制相機Y軸方向的向量，也就是UVN相機模型，UVN比較容易定義相機的朝向，類似LookAt的功能，所以這裡我們採用這種方式定義我們的相機位置和朝向。給定了相機位置和注視點位置，我們就能求得視方向向量N，然後我們根據給定的上向量V（只是輸入臨時用的，不是最終的V，輸入的V在VN平面沒有權重，因為N已經確定了視方向，只有UV平面上可能有權重，所以需要重新計算一個僅影響Roll的角），通過向量叉乘得到一個Cross(N，V)得到右向量U，最終我們再用Cross(N，U）得到真正的V，三者都需要Normalize。這樣，我們就構建出了相機所在的空間基準座標系。

我們要的是WorldToCamera的變換，不過，對一個點做一個變換，相當於對其所在座標系做逆變換，所以我們只要求出整體變換的逆矩陣即可。比如上面的變換稱之為WTC，上面的變換包括一個旋轉R和平移T，那麼我們要求的WTC^-1 (表示逆)=（RT）^-1 = （T^-1）（ R^-1）。我們拆開來看：

先是旋轉矩陣的逆，其實上面的計算，我們構建的UVN就是R矩陣了（把相機轉換到世界空間，但是在第四行沒有分量，換句話說就是3X3的矩陣，沒有位移，也沒有縮放，那麼就只有旋轉），下面一步就是求R的逆。矩陣正常求逆的運算是很費的，所以一般來說要避免直接求逆，因為3X3的旋轉矩陣其實是一個正交矩陣（各行各列都是單位向量，並且兩兩正交，可以把上一節的旋轉矩陣每個看一遍，抽出左上角3X3部分）。正交矩陣的重要性質就是MM^T (轉置)= E（單位矩陣），進一步推導就是M ^ T = M ^ -1，所以上面的旋轉矩陣的逆實際上就是它的轉置。轉置的話，我們只需要沿著對角線把資料互換一下，計算量比起求逆要小得多。 

接下來是平移矩陣的逆，這個其實不需要去推導，比如向量按照（tx，ty，tz）進行了平移變換，那麼對它的逆變換其實就是取反（-tx，-ty，-tz）。

最終兩個矩陣以及相乘結果如下，其中T = （tx，ty，tz），UVN同理：

我們直接結果構建最終的矩陣，避免多一次矩陣運算，程式碼如下：

Matrix ApcDevice::GenCameraMatrix(const Vector3& eyePos, const Vector3& lookPos, const Vector3& upAxis)
{
	Vector3 lookDir = lookPos - eyePos;
	lookDir.Normalize();

	Vector3 rightDir = Vector3::Cross(upAxis, lookDir);
	rightDir.Normalize();

	Vector3 upDir = Vector3::Cross(lookDir, rightDir);
	upDir.Normalize();

	//構建一個座標系，將vector轉化到該座標系，相當於對座標系進行逆變換
	//C = RT,C^-1 = (RT)^-1 = (T^-1) * (R^-1),Translate矩陣逆矩陣直接對x,y,z取反即可；R矩陣為正交矩陣，故T^-1 = Transpose(T)
	//最終Camera矩陣為(T^-1) * Transpose(T)，此處可以直接給出矩陣乘法後的結果，減少執行時計算
	float transX = -Vector3::Dot(rightDir, eyePos);
	float transY = -Vector3::Dot(upDir, eyePos);
	float transZ = -Vector3::Dot(lookDir, eyePos);
	Matrix m;
	m.value[0][0] = rightDir.x;  m.value[0][1] = upDir.x;  m.value[0][2] = lookDir.x;  m.value[0][3] = 0;
	m.value[1][0] = rightDir.y;	 m.value[1][1] = upDir.y;  m.value[1][2] = lookDir.y;  m.value[1][3] = 0;
	m.value[2][0] = rightDir.z;  m.value[2][1] = upDir.z;  m.value[2][2] = lookDir.z;  m.value[2][3] = 0;
	m.value[3][0] = transX;		 m.value[3][1] = transY;   m.value[3][2] = transZ;	   m.value[3][3] = 1;
	return m;
}

透視投影矩陣構建

接下來的投影階段是3D向2D轉換的一個重要的步驟（並不是這一步就轉），同時也是後續CVV裁剪，ZBuffer，透視紋理校正的基礎，這裡我們暫且不考慮正交投影，直接來看透視投影。上文我們提到，為了更好地變換，用4X4矩陣，進而引入齊次座標的概念，但是實際上，齊次座標系真正的作用在於透視投影變換。

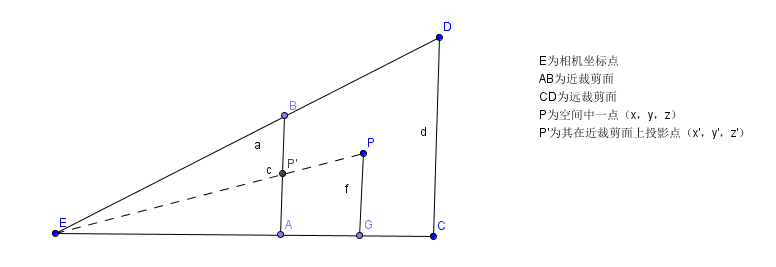
透視投影的主要知識點在於三角形相似以及小孔呈像，透視投影實現的就是一種“近大遠小”的效果，其實投影后的大小（x，y座標）也剛好就和1/Z呈線性關係。首先看下面一張圖：

上圖是一個視錐體的截面圖（只看x，z方向），P為空間中一點（x，y，z），那麼它在近裁剪面處的投影座標假設為P’(x'，y'，z’)，理論上來說，呈像的面應該在眼睛後方才更符合真正的小孔呈像原理，但是那樣會增加複雜度，沒必要額外引入一個負號（此處有一個裁剪的注意要點，下文再說），只考慮三角形相似即可。即三角形EAP’相似於三角形EGP，我們可以得到兩個等式：

x’/ x = z’/ z => x’= xz’/ z  

y’/ y = z’/ z => y’= yz’/ z

由於投影面就是近裁剪面，那麼近裁剪面是我們可以定義的，我們設其為N，遠裁剪面為F，那麼實際上最終的投影座標就是：

（Nx/z，Ny/z，N）。

投影后的Z座標，實際上已經失去作用了，只用N表示就可以了，但是這個每個頂點都一樣，每個頂點帶一個的話簡直是暴殄天物，浪費了一個珍貴的維度，所以這個Z值會被儲存一個用於後續深度測試，透視校正紋理對映的變換後的Z值。

這個Z值，還是比較有說道的。在透視投影變換之前，我們的Z實際上是相機空間的Z值，直接把這個Z存下來也無可厚非，但是後續計算會比較麻煩，畢竟沒有一個統一的標準。既然我們有了遠近裁剪面，有了Z值的上下限，我們就可以把這個Z值對映到[0,1]區間，即當在近裁剪面時，Z值為0，遠裁剪面時，Z值為1（暫時不考慮reverse-z的情況）。首先，能想到的最簡單的對映方法就是depth = （Z（eye） - N）/ F - N。but，這種方案是不正確的（需要參考下文關於光柵化資料插值的內容，此處先給出結論，我認為這個1/z在光柵化階段解釋更為合適）：透視投影變換之後，在螢幕空間進行插值的資料，與Z值不成正比，而是與1/Z成正比。所以，我們需要一個表示式，可以使Z = N時，depth = 0，Z = F時，depth = 1，並且需要有一個z作為分母，可以寫成（az + b）/z，帶入上述兩個條件：

（N * a  + b） / N = 0   =>  b = -an

（F * a  +  b） / F = 0   =>   aF + b = F => aF - aN = F

進而得到： a = F / （F - N） b = NF / （N - F）

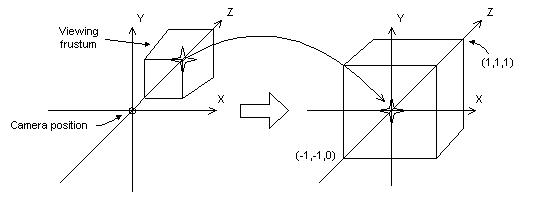
最終其實視錐體被變換為NDC，但是實際上我們一般是先不進行透視除法，那麼就稱之為CVV（此處不要過度糾結這兩個概念，下文再去解釋）過程如下圖（DX文件附圖）所示（下圖是DX模式，左手系，NDC中Z區間是0到1，也是本文使用的模式；GL的話NDC中Z是-1到1，而且是右手系，二者最終推匯出的透視投影矩陣是有差異的），主要思想就都是對映，把一個區間對映到另一個區間：

我們已經把Z值，進行了對映，秉承著對映大法好的觀點，我們再把X和Y進行一下對映，上面我們已經計算出投影后的座標值是（Nx/z，Ny/z，N）。假設近裁剪面上下分別為U，B，左右分別為L，R，我們要把原始的區間對映到[-1，1]區間。我們以X軸為例進行推導，最終X投影點對映到NDC的座標假設為Xndc，那麼對映公式如下：

Xndc - （-1） / （1 - （-1）） = （XN / Z - L) / （R - L）

計算該公式得到Xndc = 2XN / Z（R - L） - （R + L）/ （R - L）

同理Yndc  = 2YN / Z（T - B） - （T + B） / （T - B）

這樣，我們就可以得到了XYZ三個方向在NDC空間的座標。

下面在來解釋一下NDC和CVV，所謂NDC，全稱為Normalized Device Coordinates，也就是標準裝置空間，為何要引入這樣一個空間呢，主要在於我們使用不同的裝置，解析度可能都不一樣，實際在寫shader的時候，沒辦法根據解析度進行調整，而通過這樣一個空間，把x，y對映到（-1,1）區間，z對映到（0,1）區間（OpenGL是（-1,1）），在下一步螢幕座標對映時再根據螢幕解析度生成畫素真正應該在的位置，這樣可以省掉很多裝置適配的問題，讓我們在寫shader的時候一般不需要考慮螢幕解析度的問題（有時候有，主要是全屏後處理時螢幕寬高的比例，我之前在螢幕水波紋效果中實現就遇到了這樣的問題）。

再來看一下CVV，CVV全稱為Canonical View Volume，即規則觀察體。其實上面的變換最終的座標應該是NDC的，但是為了更方便地做一些其他的操作，主要是CVV裁剪，引入了一個新的空間，這個空間主要是沒有NDC空間的座標沒進行除以w計算，也就是說CVV空間的頂點還是齊次空間下的，除了w之後才會變為NDC空間，兩者的差距主要是是否除以了w。個人理解：CVV只是用齊次座標系表示了的NDC（如果我的理解不正確，還希望您及時指出我的錯誤）。

關於CVV裁剪，下文再講，我們還是回到透視投影矩陣：

我們既然要CVV空間，也就是齊次裁剪空間下的頂點，所以我們剛好可以把上文得到的投影點座標的每個元素的除以Z變換成W分量的Z，然後XYZ分量下的除以Z就可以去掉了，也就是說用齊次空間表示一下最終的投影點座標：

P’（NX，NY，aZ + b，Z）帶入上面的推導結果得到透視投影矩陣：

上面的矩陣是一個通用的矩陣，但是實際上我們絕大多數情況用的矩陣都是一個特殊情況的矩陣，也就是我們的相機剛好在視錐體中間，上下左右對稱，那麼R和L對稱，T和B對稱，兩者相加都等於0，而R-L和T-B我們就可以用一個寬度和高度來表示，簡化後的矩陣如下：

下面我們再考慮一下怎樣更加優雅地表示這個矩陣（換句話說就是參考一下DX和GL真正的介面）。我們一般來說，給定一個

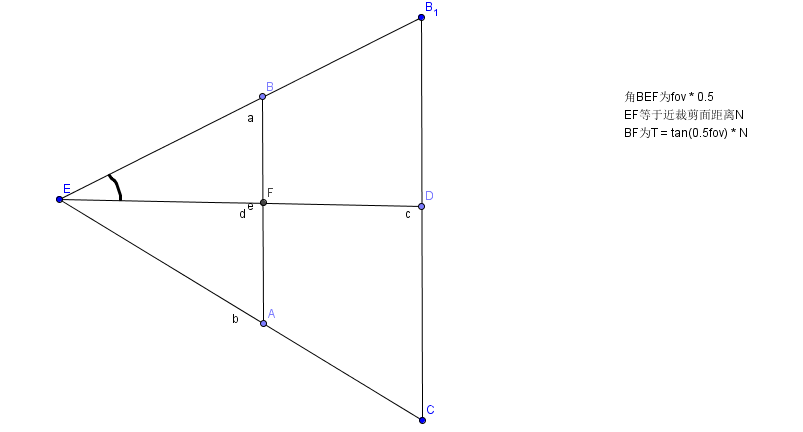
FOV角度，N近裁剪面，F遠裁剪面，Aspect螢幕寬高比即可，如下圖：

那麼BF也就是的高度就是tan（0.5*fov）* N 最終的H = 2 tan（0.5fov）*N，最終的W = Aspect * H。帶入上述矩陣：

2N/H = 2N/2tan（0.5fov）N = 1/tan（0.5fov） = cot（0.5fov）

2N/W = 1/（Aspect * tan（0.5fov）） = cot（0.5fov）/Aspect

最終矩陣結果如下，暫且還是以tan表示：

程式碼如下：

Matrix ApcDevice::GenProjectionMatrix(float fov, float aspect, float nearPanel, float farPanel)
{
	float tanValue = tan(0.5f * fov * 3.1415 / 180);

	Matrix proj;
	proj.value[0][0] = 1.0f / (tanValue * aspect);
	proj.value[1][1] = 1.0f / (tanValue);
	proj.value[2][2] = farPanel / (farPanel - nearPanel);
	proj.value[3][2] = -nearPanel * farPanel / (farPanel - nearPanel);
	proj.value[2][3] = 1;
	return proj;
}

這裡，我們只是進行了透視投影變換的第一步，將頂點轉化到齊次裁剪空間，因為並沒有進行透視除法，所以還沒有所謂的投影。第二步是透視除法，但是中間一般還會穿插一步，CVV裁剪。

啊，終於寫完了透視投影矩陣的變換，實際上這個矩陣結果只有幾個數，然而背後的數學推導還是比較複雜的。有了P矩陣，我們最終用來變換的矩陣就都完成了。

CVV裁剪

經過了透視變換，座標被變換到CVV空間，此時仍然是齊次座標，我們正常應該是判斷在裁剪的立方體內，不過齊次座標我們也就是直接比較xyz值和w的值即可，DX模式的話，z需要比較0和w。這個是非常重要的，因為我們預設為了方便是把投影平面放到了眼睛前面，但是真的有在投影平面後面的東西，如果不剔除z<0的內容，就會導致這一部分按照不對的透視公式進行計算導致結果錯誤。而且更重要的一點在於，相機空間z = 0的時候（也就是齊次空間的w = 0）的這種情況，在我們透視除法的時候會有除0的問題。所以要把這個剔除掉。

比如一個齊次空間的頂點，我們可以按照上述方式判斷其是否在CVV內：

inline bool ApcDevice::SimpleCVVCullCheck(const Vertex& vertex)
{
	float w = vertex.pos.w;
	if (vertex.pos.x < -w || vertex.pos.x > w)
		return true;
	if (vertex.pos.y < -w || vertex.pos.y > w)
		return true;
	if (vertex.pos.z < 0.0f || vertex.pos.z > w)
		return true;
	return false;
}

CVV裁剪個人感覺是一個比較有爭議的地方，現代的GPU到底如何去做裁剪，我不敢妄加推測，看了知乎上大佬們的討論，也是分為幾個派別。有認為裁剪的，有人為只剔除不裁剪的。不過個人倒比較贊同，重新構建一個三角形對於GPU來說還不如把整個三角形都畫了好，畢竟實際運用時，三角形的密度很大，面積很小，都繪製了也要比裁剪可能還省。對於CVV中比較好處理的主要在於我們可以在透視除法前就把完全不可見的三角形直接剔除掉。所以我只實現了最簡單的三頂點均不在CVV內剔除的方案（好吧，為偷懶找了個理由o(╯□╰)o）。

實現了CVV裁剪，其實還是蠻爽的，尤其是本身沒有場景管理，視錐體裁剪的話，提交上來的所有內容都要繪製，如果本身不可見的話，那直接就咔掉了。測試的話，直接渲染立方體，幀率25左右，立方體在CVV外不開裁剪，幀率100多些（有視口範圍判斷），立方體在CVV外開裁剪，幀率999+直接爆表 。

透視除法與螢幕座標對映

經過了透視投影變換，CVV裁剪，現在我們的頂點座標都在齊次裁剪空間，下一步就是真正地進行透視除法了，經過了這一步才真正算是完成了透視投影變換。其實這個操作比較簡單，因為計算在透視投影矩陣的構建中我們都推導過了，乘過Project矩陣的頂點，w座標就不會是預設的1了。因為我們把Z值存了進去，此時我們將三個分量都除以Z，就得到了透視變換後的NDC座標了。

馬上就可以和我們之前進行的在螢幕上繪製三角形聯絡起來了，中間只差了一步，那就是螢幕座標對映。上文介紹過，NDC的作用就是為了讓我們計算時不需要考慮螢幕解析度相關的問題，因為DX或者GL替我們做了，軟渲染的話，我們就需要自己做這一步。

我們建立視窗的時候，會給一個視窗的寬度和高度（RT類似），既然我們得到了NDC空間的座標值了，並且知道了螢幕的長和寬（解析度），那麼，是時候進行一波映射了。對映大法好啊！

NDC是（-1,1）區間（現在暫時只考慮X，Y），我們要把它對映到螢幕的（0，width）和（0，height）區間即可。先看X方向：首先，我們從（-1,1）區間對映到（0,1）區間，也就是（v.x / v.w + 1）* 0.5 * deviceWidth。Y方向，螢幕實際的座標是左上角為（0,0）點，與我們的NDC是反過來的，所以對映到（0,1）區間後，還需要反向一下，改為（1-screendCoord）* deviceHeight。程式碼如下，進行了透視除法&螢幕空間對映：

float reciprocalW = 1.0f / v.w;
float x = (v.x * reciprocalW + 1.0f) * 0.5f * deviceWidth;
float y = (1.0f - v.y * reciprocalW) * 0.5f * deviceHeight;

這裡的x，y就是經過了上述所有變換後，最終在螢幕上的座標點。下面我們整合一下整個3D變換的過程，最終螢幕座標v' = vFinalMatrix => vMVP => vSRTVP => vSRxRyRzTVP，程式碼如下：

Matrix ApcDevice::GenMVPMatrix()
{
	Matrix scaleM = GenScaleMatrix(Vector3(1.0f, 1.0f, 1.0f));
	Matrix rotM = GenRotationMatrix(Vector3(0, 0, 0));
	Matrix transM = GenTranslateMatrix(Vector3(0, 0, 0));
	Matrix worldM = scaleM * rotM * transM;
	Matrix cameraM = GenCameraMatrix(Vector3(0, 0, -5), Vector3(0, 0, 0), Vector3(0, 1, 0));
	Matrix projM = GenProjectionMatrix(60.0f, (float)deviceWidth / deviceHeight, 0.1f, 30.0f);

	return worldM * cameraM * projM;
}

void ApcDevice::DrawTrangle3D(const Vector3& v1, const Vector3& v2, const Vector3& v3, const Matrix& mvp)
{
	Vector3 vt1 = mvp.MultiplyVector3(v1);
	Vector3 vt2 = mvp.MultiplyVector3(v2);
	Vector3 vt3 = mvp.MultiplyVector3(v3);

	Vector3 vs1 = GetScreenCoord(vt1);
	Vector3 vs2 = GetScreenCoord(vt2);
	Vector3 vs3 = GetScreenCoord(vt3);

	DrawTrangle(vs1.x, vs1.y, vs2.x, vs2.y, vs3.x, vs3.y);
}

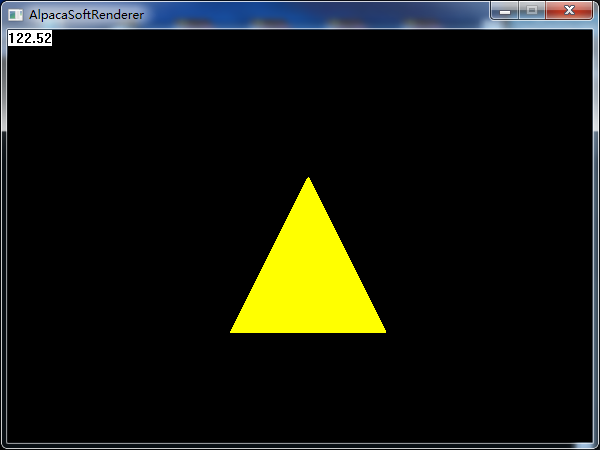
我們把MVP的計算整個抽取出來，每個物件計算一次即可，物件所有的三角形運用同一個MVP變換，即每個三角形逐頂點與MVP矩陣相乘，然後進行視口對映即可。這樣，我們就得到了一個可以變換的三角形（雖然看起來和上面一樣，然而這的確是一個有故事的三角形，因為他不是直接顯示在螢幕上的，而是歷經了無數次計算，才顯示到了螢幕上）：

來一張動圖，應用了旋轉和平移變換（有故事的三角形自然多了一些能力，比如移動，旋轉，縮放，隨著相機位置移動的近大遠小效應）：

光柵化資料插值與仿射紋理對映

直到目前為止，我們雖然可以在螢幕上看到三角形了，並且可以運用各種變換，但是我們的三角形沒有任何其他資料，僅有一個位置資訊，這是十分令人不爽的，尤其是我這個視覺動物，憋了半天終於畫出了個三角形，然而還木有顏色，簡直是不能忍了！我們要給它加點料！要有更好的表現，我們就要給頂點加一些屬性，最常見的，也是最容易的，就是顏色啦。我們給每個頂點增加一個頂點色，儲存在頂點中。but，我們這時候應該意識到一個問題，我們的三角形只有三個點，而最終顯示在螢幕上的可是無數個畫素啊，其中的資料要怎麼樣得到呢？

比如我們正常寫shader的時候，經常會定義一個v2f之類的結構體，用來從vertex階段傳遞到fragment階段，vertex階段我們只考慮逐頂點計算的值就可以了，傳遞v2f，到fragment階段，自動就可以在輸入時取到每個v2f在fragment階段的值，這個資料實際上是渲染管線幫我們自動處理了。所運用到的知識點其實也是非常簡單的，就是插值（Lerp）。

來看一維的插值程式碼，也就是我們經常用的Lerp函式：

float LerpFloat(float v1, float v2, float t){ return v1 + (v2 - v1) * t;}

其實非常簡單，我們給一個（0，1）的插值控制函式，就可以完成從v1，v2之間的插值了，當t=0時，為v1，當t=1時為v2。

那麼，在三角形設定好之後，三個頂點的資料是一定的，接下來要從上到下繪製掃描線，我們每次要繪製掃描線的時候，首先要獲得掃描線兩側端點的資料值，掃描線的兩側端點的值在我們求解方程的時候可以得到，也就能求出該點在端點所在的邊所處的值，此處是從上到下，那麼我們就用y作為插值係數，以即每一點的t = （y - y0）/ （y2 - y0），然後我們就可以用這個係數去在頂點和底點兩個點之間插值得到當前線上掃描線起始點和結束點的顏色值。掃描線本身也是同理，已知左右兩點的顏色值，每次前進一個畫素，都可以求出當前t = （x - x0） / （x1 - x0）作為插值係數。比如我們給上面的三角形增加一個頂點色，通過插值就可以得到如下的效果：

有了顏色，我們的三角形就好看了不少。需求總是有的，能不能再好看一點呢？既然程式碼寫不出來，那就貼張圖上去吧！（我想這應該也是前輩們發明紋理對映的初衷吧）。還是同一個問題，我們只有頂點資料，也就是美術同學展uv得到的座標值，存在頂點中。畫素上全靠插值，那麼要想貼上一張圖，我們應該有的其實是這一個畫素點應該取樣的紋理座標也就是uv值，還是一樣的思路，我們補全插值的計算和頂點上的uv資料。然後用windows自帶的功能讀入一張bmp貼圖，然後構建一個二維陣列，把這個貼圖的每個畫素逐步拷入陣列就可以了。取樣時，我們計算出uv值，然後依然是對映大法好，因為uv是（0,1）區間，我們把這個區間對映到畫素陣列的大小，然後就可以用這個index去紋理陣列中取樣該點的顏色了。其實在這一步也可以做一點小文章，比如傳過來的uv是非（0,1）區間的，那麼邊界的顏色怎麼給，如果我們直接截斷，那麼就是clamp，也可以取餘數那就是repeat，還可以實現mirror等模式。這裡我就直接Clamp了。下面是Texture類中兩個主要的函式：

void Texture::LoadTexture(const char* path)
{
	HBITMAP bitmap = (HBITMAP)LoadImage(NULL, path, IMAGE_BITMAP, width, height, LR_LOADFROMFILE);
	
	HDC hdc = CreateCompatibleDC(NULL);
	SelectObject(hdc, bitmap);
	
	for (int i = 0; i < width; i++)
	{
		for (int j = 0; j < height; j++)
		{
			COLORREF color = GetPixel(hdc, i, j);
			int r = color % 256;
			int g = (color >> 8) % 256;
			int b = (color >> 16) % 256;
			Color c((float)r / 256, (float)g / 256, (float)b / 256, 1);
			textureData[i][j] = c;
		}
	}
}

Color Texture::Sample(float u, float v)
{
	u = Clamp(0, 1.0f, u);
	v = Clamp(0, 1.0f, v);
	//暫時直接採用clamp01的方式取樣
	int intu = width * u;
	int intv = height * v;
	return textureData[intu][intv];
}

搞一個自己的頭像試一下紋理對映：

看起來好多了，是不是大功告成了呢？其實並不是，因為這一節忽略了一個重要的問題，導致我們所有的插值其實都是錯誤的，上面看起來沒有問題，是因為僅僅看起來可能是對的。

1/Z的問題與透視校正紋理對映

我們把上面的面片，沿著Y軸旋轉45度，再看一下效果：

哦，偉大的蠍同志腫麼變成了小短腿。。。簡直玷汙了我的偶像（我得趕快改好）。如果我們換一個貼圖，那麼這個問題將暴露得更加明顯：

這是個什麼鬼。。。我貼上去的可是一個方方正正的網格貼圖：

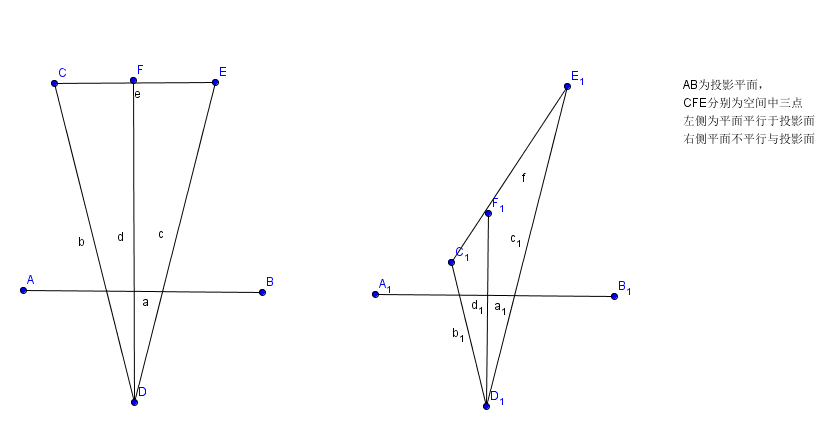
那麼，問題應該比較明確了，就出在透視上。來看一張圖解釋一下上面的現象：

右側的三角形是我直接複製過去的，唯一的區別就在於左側CFE平面平行於近裁剪面，而右側把CFE整個一條線拉歪，使C接近近裁剪面。二者在最終投影在近裁剪面的位置完全相同，但是實際上在三維空間位置是相差甚遠的。

先祭出兩篇大佬的推導：一篇幾何證明，一篇代數證明。我數學不好，只能膜拜這些大佬了。主要證明的就是在投影空間的值與1/z成正比。

我們存在頂點中的資料，頂點顏色，頂點上uv的座標等內容，其實都是在模型空間下製作的，換句話說，這些值實際上應該在模型空間下進行插值計算，但是投影是一個損失維度的變換，我們單純地用最終二維螢幕上的位置距離去插值，如果Z全都一致，那沒有影響，在投影平面均勻變換的值，對應相機空間（推回模型空間也一樣）也是均勻變換的。但是像右圖，在投影平面兩段相同距離對應相機空間的距離就不同了。

我們在推導投影矩陣的時候，得到過投影點的座標（Nx/z，Ny/z，N），換句話說，投影后的X’本身就是與1/Z呈線性關係的，然後我們還知道uv座標與x呈線性關係，實際上就是uv座標與1/z呈線性關係，那麼通過這樣一個方式，我們在三角形進行設定時，強行把uv除以一個z，那麼此時uv就變成了uv/z，這個值是與投影后的nx/z呈線性關係的，也就是說我們可以在螢幕空間根據距離進行線性插值得到一點上的確切的uv/z值。不過還有一個問題，我們得到了uv/z，還需要把uv還原，也就是得到uv，我們還需要再求出當前點的1/z值，這個值被我們存在了z座標上，我們在每個點取樣的時候，再把z乘回去，就得到了這一點真正的uv座標值（最後除以z和w其實效果差不多，兩者其實也是線性關係）。

inline void ApcDevice::PrepareRasterization(Vertex& vertex)
{
	//透視除法&視口對映
	//齊次座標轉化，除以w，然後從-1,1區間轉化到0，1區間，+ 1然後/2 再乘以螢幕長寬
	float reciprocalW = 1.0f / vertex.pos.w;
	vertex.pos.x = (vertex.pos.x * reciprocalW + 1.0f) * 0.5f * deviceWidth;
	vertex.pos.y = (1.0f - vertex.pos.y * reciprocalW) * 0.5f * deviceHeight;
	//將其他資料轉化為1/z
	vertex.pos.z *= reciprocalW;
	vertex.u *= vertex.pos.z;
	vertex.v *= vertex.pos.z;
}

在取樣時，使用了：

int errorValue = dy2 - dx;
for (int i = 0; i <= dx; i++)
{
	float t = (x - x0) / (x1 - x0);
	float z = Vertex::LerpFloat(v0.pos.z, v1.pos.z, t);
	float realz = 1.0f / z;
	float u = Vertex::LerpFloat(v0.u, v1.u, t);
	float v = Vertex::LerpFloat(v0.v, v1.v, t);	
	Color c = tex->Sample(u * realz, v * realz);
	DrawPixel(x, y, c);
	x += stepx;
	errorValue += dy2;
	if (errorValue >= 0)
	{
		errorValue -= dx2;
		y += stepy;
	}
}

經過透視校正紋理取樣後的效果：

logo的效果也正常啦：

ZBuffer演算法

人的需求總是無限的，貼上了圖，還是感覺不夠爽，畢竟不是一個立體的東西，只是個面片，下面我決定搞個模型進來。不過我不打算引入第三方庫，匯入fbx那不是軟渲染干的事兒了，這個東西在opengl玩更好。所以我手擼了個立方體資料，直接寫個頂點快取，每個點加個uv資料。然後坐等我的立方體出現：

額，好像。。。哪裡不太對。。。立方體面之間的遮擋關係錯亂了。換句話說，我們沒有深度測試，沒有辦法保證立方體面渲染的順序，我們需要的是畫素精度的深度保證。下面來加一個ZBuffer。

其實ZBuffer的思想比較簡單，就是在逐畫素增加一個快取，每次繪製的時候，把當前深度也儲存進這個buffer，下次再繪製該畫素的時候，先判斷一下當前畫素的z值，如果比該值小或相等的話，說明離得更近（僅考慮ZTest LEqual）。這種情況下就可以更新當前畫素點的顏色值，並且可以選擇更新深度快取。

我們先申請一塊螢幕大小的float型別記憶體：

zBuffer = new float*[deviceHeight];
for (int i = 0; i < deviceHeight; i++)
{
	zBuffer[i] = new float[deviceWidth];
}

然後每次渲染之前，除掉ClearColorBuffer外，還要把DepthBuffer也Clear掉：

void ApcDevice::Clear()
{
	BitBlt(screenHDC, 0, 0, deviceWidth, deviceHeight, NULL, NULL, NULL, BLACKNESS);
	//ClearZ
	for (int i = 0; i < deviceHeight; i++)
	{
		for (int j = 0; j < deviceWidth; j++)
		{
			zBuffer[i][j] = 0.0f;
		}
	}
}

每次繪製時進行深度判斷，深度檢測失敗不進行繪製，深度檢測成功此處預設開啟ZWrite：

bool ApcDevice::ZTestAndWrite(int x, int y, float depth)
{
	//上面只進行了簡單CVV剔除，所以還是有可能有超限制的點，此處增加判斷
	if (x >= 0 && x < deviceWidth && y >= 0 && y < deviceHeight)
	{
		if (zBuffer[y][x] <= depth)
		{
			zBuffer[y][x] = depth;
			return true;
		}
	}
	return false;
}

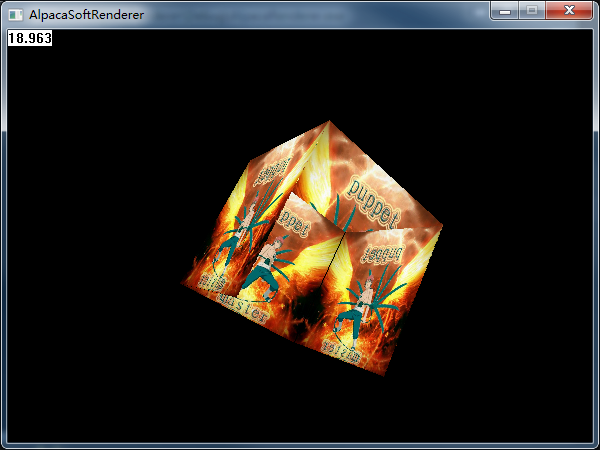
有了深度快取，我們的立方體就完整啦：

深度快取，我採用的是1/Z，所以上面的深度預設為0表示無限遠。為了更好的效率，我的ZTest實際上放在了計算掃描線時每次插值計算出Z之後立刻就進行深度檢測，其實類似於Early-Z，而不是實際上真正渲染時的ZCheck，因為我沒有考慮Alpha Test的情況，也不需要考慮分支的問題，直接Cull掉是效能最好的。

int errorValue = dy2 - dx;
for (int i = 0; i <= dx; i++)
{
	float t = (x - x0) / (x1 - x0);
	float z = Vertex::LerpFloat(v0.pos.z, v1.pos.z, t);
	float realz = 1.0f / z;
	if (ZTestAndWrite(x, y, realz))
	{
		float u = Vertex::LerpFloat(v0.u, v1.u, t);
		float v = Vertex::LerpFloat(v0.v, v1.v, t);
		//Color c = Color::Lerp(v0.color, v1.color, t);
		Color c = tex->Sample(u * realz, v * realz);
		DrawPixel(x, y, c);
	}

	x += stepx;
	errorValue += dy2;
	if (errorValue >= 0)
	{
		errorValue -= dx2;
		y += stepy;
	}
}

關於深度，其實還有很多可以玩的，不過這麼好玩的東西，還是另起一篇blog吧。

最後，再來一張動圖：

總結

本文主要實現了基本的光柵化渲染器的一些常見的特性，MVP矩陣變換，簡單CVV剔除，視口對映，光柵化，透視校正紋理取樣等等。目前還有基本的光照，背面剔除，線框渲染，相機控制等幾個是我打算加的。有些演算法肯定很古老，而且GPU的具體實現我不敢妄加揣測，填軟渲染的坑主要是為了學習的目的，加深一下對渲染知識的理解。其實實現的過程還是蠻有意思的（有點找到了幾年前寫了第一個命令列版本的2048的那種樂趣，當時自己玩了半宿，一邊玩一邊手舞足蹈，室友以為我瘋了呢），很久不寫的C++又溫習了一下，再一個方面就是需要考慮優化了，讓我清晰地意識到逐畫素計算是真的很費很費，面片貼臉的時候基本就跑不動啦！！！專案從開始寫的時候，只有一個三角形沒經過變換，沒有采樣，FPS上百，逐漸增加特性之後幀率一度掉到了個位數，後來稍微優化了一下，穩定在了20-25幀，還是有很大的優化的空間的。

程式碼的話直接開源吧，第一次用Git，如果能您賞個星星什麼的就更好啦。本人才疏學淺，如果您發現了什麼問題，還望批評指正。