機器學習升級版第七期——第二課(概率論與貝葉斯先驗)
阿新 • • 發佈:2019-01-05
本總結僅為防止遺忘而作
常見的分佈有
關於具體分佈的理論部分在此不做過多闡述,可自行查閱資料。其中負二項分佈
下面給出生活中具體的例子
對於上面的例子,若11分制,劉詩雯若獲勝那麼最後一球肯定是劉詩雯贏的,則對於公式
x=11,r=6,最後一球為劉詩雯贏的,那麼前十球中劉詩雯贏5球,即有上面的公式。
下面附上python執行的程式碼:
import numpy as np from scipy import special if================================================================== 接著生活中現象對應的常見分佈: 泊松分佈__name__ =='__main__': method='strict' #暴力模擬 if method =='simulation': p = 0.6 a,b,c = 0,0,0 t,T = 0,1000000 while t < T: a = b = 0 while (a <= 11) and (b <= 11): if np.random.uniform()<p: a += 1 else: b += 1 if a>b: c += 1 t += 1 print(float(c)/float(T)) #直接計算 elif method == 'simple': answer =0 p = 0.6 N = 11 for x in np.arange(N): #x為對手得分 answer += special.comb(N+x-1,x)*((1-p)**x)*(p**N) #scipy.special.comb(N, k) 二項分佈 print(answer) #The number of combinations of N things taken k at a time. #嚴格計算 else: answer = 0 p = 0.6 N = 11 for x in np.arange(N-1): #x為對手得分 11:9 11:8 11:7 ... answer += special.comb(N+x-1,x)*((1-p)**x)*(p**N) print(answer) p10 = special.comb(2*(N-1),N-1)*((1-p)*p)**(N-1) # 10:10的概率 t = 0 for n in np.arange(100): t += (2*p*(1-p))**n*p*p answer += p10*t print(answer)



====================================================================================================

Beta 分佈與gamma函式有關,Beta 分佈的期望為α/(α+β)
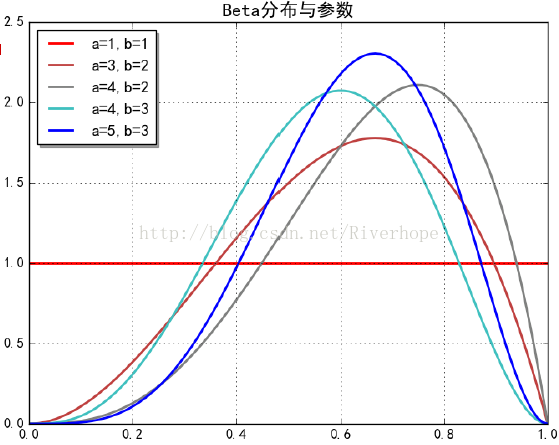
==================================================================================== 另一個重要的概念

從標題上看,是“指數分佈族(exponential family)”,不是“指數分佈(exponential distribution)”,這是兩個不同的概念。在概率論和統計學中,它是一些有著特殊形式的概率分佈的集合,包括許多常用的分佈,如normal分佈、exponential distribution、bernouli、poission、gamma分佈、beta分佈等等。指數分佈族為很多重要而常用的概率分佈提供了統一框架,這種一般性有助於表達的方便和從更大的巨集觀尺度上理解這些分佈.
bernouli分佈可以寫為:


Gaussian分佈也屬於指數族分佈可寫為:
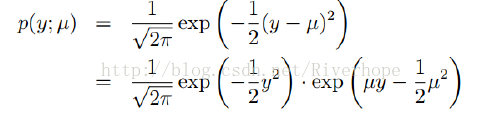

===================================================================== Pearson相關係數:

附上python程式碼
import numpy as np from scipy import stats import matplotlib as mpl import matplotlib.pyplot as plt import warnings mpl.rcParams['axes.unicode_minus'] = False mpl.rcParams['font.sans-serif'] = 'SimHei' def calc_pearson(x, y): std1 = np.std(x) #標準差 # np.sqrt(np.mean(x**2) - np.mean(x)**2) std2 = np.std(y) cov = np.cov(x, y, bias=True)[0,1] print(np.cov(x,y)) return cov / (std1 * std2) # ρ def intro(): N = 10 x = np.random.rand(N) y = 2 * x + np.random.randn(N) * 0.1 print(x) print(y) print('系統計算:', stats.pearsonr(x, y)[0]) #r是相關係數,取值[-1,1] 表示線性相關程度 # print(0.0005[0]) print('手動計算:', calc_pearson(x, y)) def rotate(x, y, theta=45): data = np.vstack((x, y)) #vstack vertical stack ,hstack horizon stack print (data) mu = np.mean(data, axis=1) mu = mu.reshape((-1, 1)) print('mu=',mu) data -= mu print ('data-mu=',data) theta *= (np.pi / 180) c = np.cos(theta) s = np.sin(theta) m = np.array((c, -s), (s, c)) print('m=',m) return np.dot(m,data) + mu def pearson(x, y, tip): clrs = list('rgbmycrgbmycrgbmycrgbmyc') plt.figure(figsize=(10, 8), facecolor='w') for i, theta in enumerate(np.linspace(0, 90, 6)): xr, yr = rotate(x, y, theta) p = stats.pearsonr(xr, yr)[0] print (calc_pearson(xr, yr)) print('旋轉角度:', theta, 'Pearson相關係數:', p) str = '相關係數:%.3f' % p plt.scatter(xr, yr, s=40, alpha=0.9, linewidths=0.5, c=clrs[i], marker='o', label=str) plt.legend(loc='upper left', shadow=True) plt.xlabel('X') plt.ylabel('Y') plt.title('Pearson相關係數與資料分佈:%s' % tip, fontsize=18) plt.grid(b=True) plt.show() if __name__ == '__main__': # warnings.filterwarnings(action='ignore', category=RuntimeWarning) np.random.seed(0) intro() N = 1000 # tip = '一次函式關係' # x = np.random.rand(N) # y = np.zeros(N) + np.random.randn(N)*0.001 # tip = u'二次函式關係' x = np.random.rand(N) y = x ** 2 + np.random.randn(N)*0.002 # # tip = u'正切關係' # x = np.random.rand(N) * 1.4 # y = np.tan(x) # # tip = u'二次函式關係' # x = np.linspace(-1, 1, 101) # y = x ** 2 # # tip = u'橢圓' # x, y = np.random.rand(2, N) * 60 - 30 # y /= 5 # idx = (x**2 / 900 + y**2 / 36 < 1) # x = x[idx] # y = y[idx] pearson(x, y, tip)生成影象為:
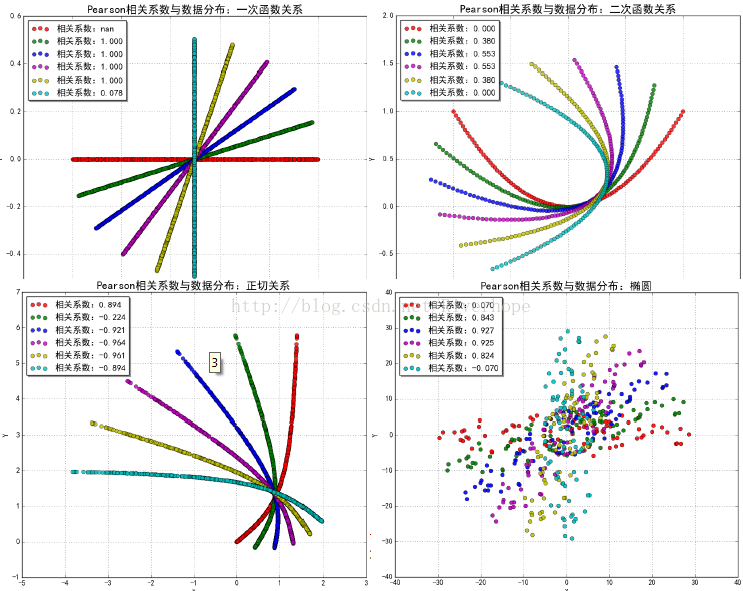
在二次函式影象中可以看出紅色線的相關係數為0,但其是具有相關性的,原因為Pearson係數在求取的過程中正負相互抵消導致為0,所以有的時候我們不用Pearson係數進行檢驗。 ======================================================================

maxP(AlD)在給定樣本的情況下,算出A結論的概率取最大,即本來我們是算哪一個結論發生概率最大,那麼這個結論是最有可能的,但在日常生活中會反著做maxP(DlA)就是當樣本給定時,我們先看發生的概率是多少,然後哪一個結論能夠使得我們這個樣本發生的概率最大我們就認為那個結論是最容易發生的。(這塊有點繞=.=),一句話就是我們想從資料找原因,其實我們是從原因看資料 最大似然估計:

對於似然函式具體求法不做闡述





