Supervised Descent Method Face Alignment 程式碼下載 和 演算法研究 之一
1 主要內容:
Supervised Descent Method and its Applications to Face Alignment演算法研究。
3本文分為幾個部分:
(1)解決什麼問題
(2)具體理論方法是什麼
(3)具體實現步驟
(1)解決什麼問題
上一篇文章newton方法,請看具體實現,
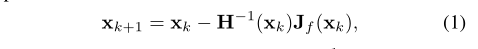
牛頓法目的是求f(x)最小值。然後改成求f’(x)=0。
迭代n次上圖公式1,直到Xk+1 - Xk收斂到0.0001
or 其他非常小大於0的值。
而公式1中 f’(x)是上圖中J(f(Xk))函式, 而f”(x)是H(Xk).
下圖為該方法:
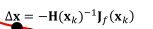
更多內容請看:上一篇牛頓法-最優方法。
我們知道牛頓法:要滿足在定義域內二次可微,hession矩陣正定。
而在計算機背景下,運用newton method有三個問題:
1 Hession矩陣在最小值的區域性是正定的,但在其他地方可能不正定。
因為只有Hession矩陣正定,初始值才能收斂到區域性值。
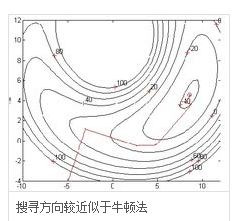
上圖可知:搜尋方法是凹方向,是梯度 or Hession矩陣的相反方向,只有Hession矩陣正定,即每個Hession矩陣每個特徵值大於零,才會沿著梯度相反方向,即沿著曲線的凹方向(梯度方向是曲線的凸方向),收斂到區域性極值點。
2Hession矩陣需要二次可微。
3Hession矩陣的維數可能很大。而Hession矩陣的逆矩陣計算的時間複雜度是O(n^3),空間複雜度O(n^2),n是矩陣維數,計算量和空間記憶體都需要很大,即使用 L-BFGS,計算成本仍然很大。
所以作者提出了a Supervised Descent Method (SDM),來求非線性的最小平方差。
在訓練階段:
通過最小化所有樣本的非線性平方差函式之和,
學習許多梯度方向組成的梯度序列。
在測試階段:
SDM minimizes 非線性平方差函式,
使用訓練時訓練的梯度方向,
再也不用計算 the Jacobian nor the Hessian矩陣 。
(2)Supervised Descent Method(SDM)具體理論原理是什麼?
這裡研究的SDM是對face alignment application.
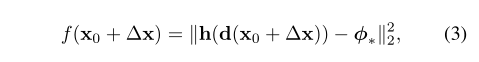
上公式中:
1 d代表一個人臉圖片的m個畫素,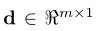
2 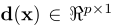
d(x)代表一個圖片的66個標點。
3 h是特徵抽取函式(比如sift特徵抽取),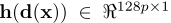
h(d(x))是在標點d(x)周圍抽取的128維的sift特徵。

4上圖
(a)圖在訓練期間,假設66個標記是已知,我們稱之為X*
(b)圖 先用檢測到人臉(藍色矩陣框),再用所有樣本平均shape,作為X0,初始化位置。
人臉匹配(face alignment),是極小化公式(3).