最近在研究人臉特徵點檢測，之前沒接觸過，有些論文雖然能看懂，但是細節的部分可能之前的論文都有提到過，就沒有再提。所以找了一篇稍微早一點的文章開始學習起來。
MATLAB版本的程式碼基本上都看懂了，不過作者可能之前做過ASM，程式碼中有一些方法沒有使用，或者使用了比較複雜的演算法，其實只使用了其中一小部分結果，看起來有點難。準備找時間自己實現一下，看了程式碼應該不算難（又立flag了，督促自己不要偷懶）。這裡先簡單的實現SDM演算法，不做人臉應用的程式碼。
簡單的說SDM演算法是牛頓法的一種改進，牛頓法在求解梯度的時候需要用到Hessian矩陣的逆以及Jacobian矩陣，在高維度的情況下這個計算量較大，而且有些情況下Hessian矩陣是不可逆的。這篇論文通過監督學習來學習Hessian矩陣的逆以及Jacobian矩陣的乘積，這樣就可以省去複雜的計算過程。

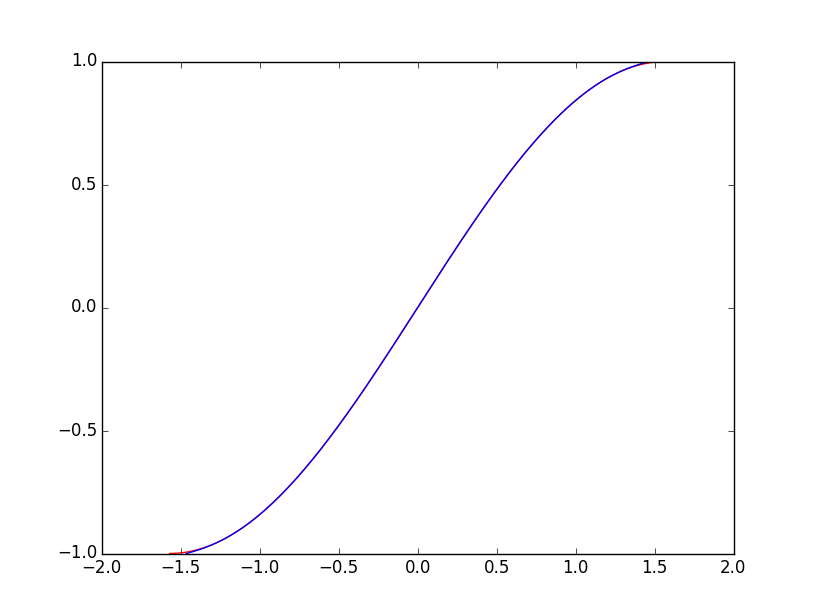
下面程式碼是SDM實現的例子，完成對曲線的擬合。擬合過程中會列印誤差值。R儲存了要學習的引數。steps是蒙特卡洛取樣的引數，取樣點間隔越小，擬合效果越好。
程式碼簡單的說就是在訓練過程中已知dx,dy，然後可以通過最小二乘訓練R，然後在Test過程中，已知dy可以通過R求解x的最優解。論文中提到了訓練引數R和b，應該可以合到一起，這裡只有引數R。

#coding:utf-8

import numpy as np
import math
import matplotlib.pyplot as plt

#取樣間距
steps = [0.25,0.025,0.0025,0.00025]

y = np.mat(np.arange(-1
 
,1,0.001))
x = np.mat(np.arcsin(y))


for i in range(len(steps)):
    #train
    R = []  #要學習的引數
    n = 10  #迭代次數，一般要多次迭代才能達到較好的效果，減小n會看到誤差增大
    y0 = np.mat(np.arange(-1,1,steps[i]))
    x0 = np.mat(np.arcsin(y0))
    x_start = np.mat([0] * x0.shape[1])
    for j in range(n):
        dx = x0 - x_start
        dy = y0 - np.sin(x_start)
        #嶺迴歸
 

        r_tmp = (dy*dy.T+np.eye(1)*0.001).I*(dy*dx.T)
        x_start = x_start + r_tmp*dy
        R.append(r_tmp)
        print np.linalg.norm(dx)    #求誤差，所有元素平方和開根
    print '--------------------'
    #test
    y_pred = y
    x_pred = np.mat([0]*x.shape[1])
    for j in range(n):
        dy = y - np.sin(x_pred)
        x_pred = x_pred + R[j]*dy
        #  += 上面一句之前用了這個，一直有問題，有點坑，對於變數python是可以這麼寫的，矩陣不可以吧

    plt.plot(np.asarray(x)[0], np.asarray(y)[0], 'r')
    plt.plot(np.asarray(x_pred)[0], np.asarray(y_pred)[0], 'b')
    plt.show()

下面是擬合的效果圖，紅色為真實曲線，藍色為訓練得到的曲線。