歡迎大家關注我們的網站和系列教程：http://panchuang.net/ ，學習更多的機器學習、深度學習的知識！

目錄：

• 常用的迴圈神經網路結構

• 多層迴圈神經網路
• 雙向迴圈神經網路
• 遞迴神經網路

• 長期依賴問題及其優化

• 長期依賴問題
• 長期依賴問題的優化

• 參考文獻

一、常用的迴圈神經網路結構

前面的內容裡我們介紹了迴圈神經網路的基本結構，這一小節裡我們介紹幾種更常用的迴圈神經網路的結構

1. 多層迴圈神經網路

多層迴圈神經網路是最容易想到的一種變種結構，它的結構也很簡單，就是在基本的迴圈神經網路的基礎上增加了隱藏層的數量。

圖1 多層迴圈神經網路結構

多層迴圈神經網路按時間展開後，每一層的引數和基本的迴圈神經網路結構一樣，引數共享，而不同層的引數則一般不會共享（可以類比CNN的網路結構）。和基本結構的迴圈神經網路相比，多層迴圈神經網路的泛化能力更強，不過訓練的時間複雜度和空間複雜度也更高。在TensorFlow裡，我們可以藉助MultiRNNCell這個類來實現深度迴圈神經網路，下面我們用一個具體的例子來演示TensorFlow中多層迴圈神經網路的實現。

示例：航班乘客人數預測

時間	乘客人數（單位：千人）
"1949-01"	112
"1949-02"	118
"1949-03"	132
"1949-04"	129
"1949-05"	121

我們將所有資料視覺化顯示：

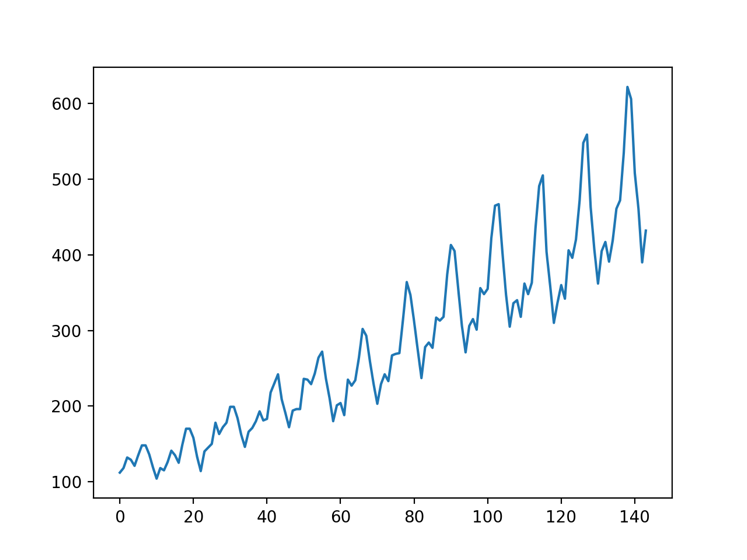
圖2 資料視覺化效果圖

從視覺化的效果可以看到資料的變化呈現週期性，對於RNN來說，學習這種很明顯的序列關係並非難事。我們定義一個多層迴圈神經網路（完整專案程式碼可以在本書配套的GitHub專案中找到）：

1	def get_cell(self):
2	    return rnn.BasicRNNCell(self.hidden_dim)
3
4	def model(self):
5	    # 定義一個多層迴圈神經網路
6	    cells = rnn.MultiRNNCell([self.get_cell() for _ in range(3)], state_is_tuple=True)
7	    # 用cells構造完整的迴圈神經網路
8	    outputs, states = tf.nn.dynamic_rnn(cells, self.x, dtype=tf.float32)
9
10	    num_examples = tf.shape(self.x)[0]
11	    # 初始化輸出層權重矩陣
12	    W_out = tf.tile(tf.expand_dims(self.W_out, 0), [num_examples, 1, 1])
13	    out = tf.matmul(outputs, W_out) + self.b_out  # 輸出層的輸出
14	    out = tf.squeeze(out)  # 刪除大小為1的維度
15	    tf.add_to_collection('model', out)
16	    return out

 

在第1行程式碼中定義了一個方法用來返回單層的cell，在第6行程式碼中，我們使用MultiRNNCell類生成了一個3層的迴圈神經網路。最終的預測結果如下圖左側所示：

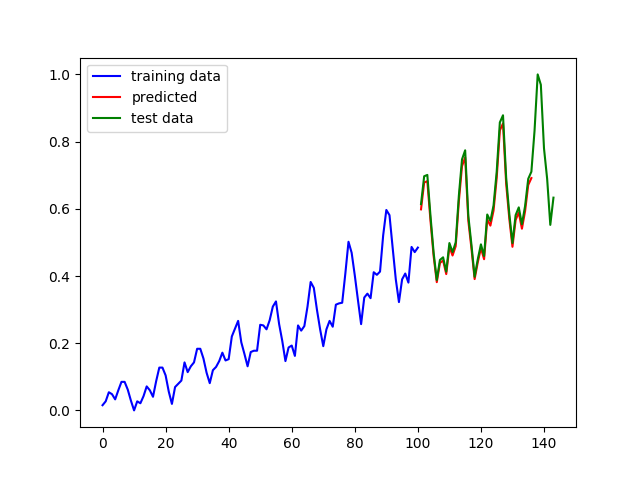
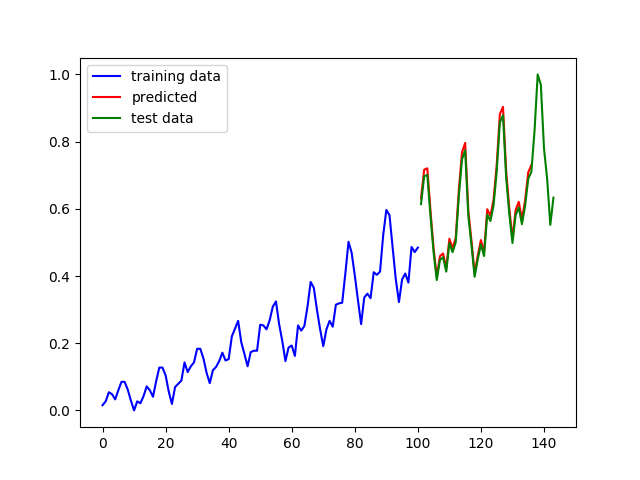
圖3多層迴圈神經網路的預測結果

上圖中，藍色線條是原始資料，綠色線條是從原始資料中劃分出來的測試資料，紅色線條是在測試資料上的預測效果，左側是多層迴圈神經網路的預測結果，右側是單層迴圈神經網路的預測結果（除網路層數不同外，其它引數均相同）。可以看到兩個預測結果都幾乎和真實資料重合，仔細比較會發現，多層迴圈神經網路的擬合效果更好一些。

2.雙向迴圈神經網路

無論是簡單迴圈神經網路還是深度迴圈神經網路[1]，網路中的狀態都是隨著時間向後傳播的，然而現實中的許多問題，並不都是這種單向的時序關係。例如在做詞性標註的時候，我們需要結合這個詞前後相鄰的幾個詞才能對該詞的詞性做出判斷，這種情況就需要雙向迴圈神經網路來解決問題。

圖4 雙向迴圈神經網路結構

圖片來源於http://www.wildml.com

雙向迴圈神經網路可以簡單的看成是兩個單向迴圈神經網路的疊加，按時間展開後，一個是從左到右，一個是從右到左。雙向迴圈神經網路的計算與單向的迴圈神經網路類似，只是每個時刻的輸出由上下兩個迴圈神經網路的輸出共同決定。雙向迴圈神經網路也可以在深度上進行疊加：

圖5 深度雙向迴圈神經網路結構

圖片來源於http://www.wildml.com

在下一章的專案實戰部分，我們會使用TensorFlow來實現深度雙向迴圈神經網路解決文字多分類問題，會結合程式碼來介紹雙向迴圈神經網路。

3.遞迴神經網路

遞迴神經網路[2]（recursive neural network，RNN）是迴圈神經網路的又一個變種結構，看它們的名稱縮寫，很容易將兩者混淆（通常我們說的RNN均特指recurrent neural network，同時也不建議將recurrent neural network說成是遞迴神經網路。一般預設遞迴神經網路指的是recursive neural network，而迴圈神經網路指的是recurrent neural network）。我們前面所介紹的迴圈神經網路是時間上的遞迴神經網路，而這裡所說的遞迴神經網路是結構上的遞迴。遞迴神經網路相較於迴圈神經網路有它一定的優勢，當然這個優勢只適用於某些特定場合。目前遞迴神經網路在自然語言處理和計算機視覺領域已經有所應用，並獲得了一定的成功，但是由於其對輸入資料的要求相對迴圈神經網路更為苛刻，因此並沒有被廣泛的應用。

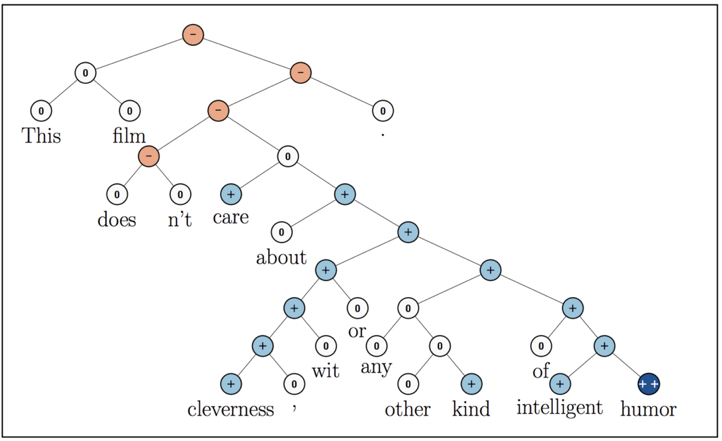
圖6 遞迴神經網路結構示意圖

二、長期依賴問題及其優化

1. 長期依賴問題

什麼是長期依賴？我們知道迴圈神經網路具有記憶能力，憑著它的記憶能力，能夠較好的解決一般的序列問題，這些序列問題的資料內部基本上都存在著一定的依賴性，例如我們在前面提到過的詞性標註的問題以及我們在演示專案裡面人工構造的二進位制資料。在有些現實問題中，資料間的依賴都是區域性的、較短時間間隔的依賴。還是以詞性標註為例，判斷一個詞是動詞還是名詞，或者是形容詞之類，我們往往只需要看一下這個詞前後的兩個或多個詞就可以做出判斷，這種依賴關係在時間上的跨度很小。

圖7 時間跨度較小的依賴關係示意圖

如上圖所示，時刻網路的輸出（上圖中到是隱藏層的輸出）除了與當前時刻的輸入相關之外，還受到和時刻網路的狀態影響。像這種依賴關係在時間上的跨度較小的情況下，RNN基本可以較好地解決，但如果出現了像圖6-12所示的依賴情況，就會出現長期依賴問題：梯度消失和梯度爆炸。

圖8 時間跨度較大的依賴關係示意圖

什麼是梯度消失和梯度爆炸？圖9是一個較為形象的描述，在深層的神經網路中，由於多個權重矩陣的相乘，會出現很多如圖所示的陡峭區域，當然也有可能會出現很多非常平坦的區域。在這些陡峭的地方，Loss函式的倒數非常大，導致最終的梯度也很大，對引數進行更新後可能會導致引數的取值超出有效的取值範圍，這種情況稱之為梯度爆炸。而在那些非常平坦的地方，Loss的變化很小，這個時候梯度的值也會很小（可能趨近於0），導致引數的更新非常緩慢，甚至更新的方向都不明確，這種情況稱之為梯度消失。長期依賴問題的存在會導致迴圈神經網路沒有辦法學習到時間跨度較長的依賴關係。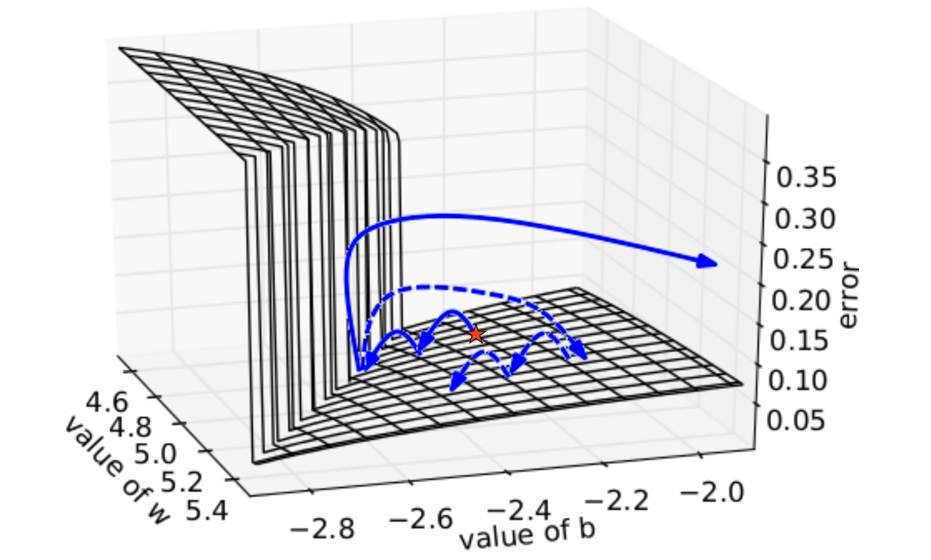

圖9 導致梯度爆炸的情況

圖片引用自Razvan Pascanu的論文：《On the difficulty of training recurrent neural networks》

正如上面所說，長期依賴問題普遍存在於層數較深的神經網路之中，不僅存在於迴圈神經網路中，在深層的前饋神經網路中也存在這一問題，但由於迴圈神經網路中迴圈結構的存在，導致這一問題尤為突出，而在一般的前饋神經網路中，這一問題其實並不嚴重。

值得注意的是，在第三章中介紹啟用函式的時候我們其實已經提到過梯度消失的問題，這是由於Sigmoid型的函式在其函式影象兩端的倒數趨近於0，使得在使用BP演算法進行引數更新的時候會出現梯度趨近於0的情況。針對這種情況導致的梯度消失的問題，一種有效的方法是使用ReLU啟用函式。但是由於本節所介紹的梯度消失的問題並不是由啟用函式引起的，因此使用ReLU啟用函式也無法解決問題。下面我們來看一個簡單的例子。

圖10 引數W在迴圈神經網路中隨時間傳遞的示意圖

如上圖所示，我們定義一個簡化的迴圈神經網路，該網路中的所有啟用函式均為線性的，除了在每個時間步上共享的引數W以外，其它的權重矩陣均設為1，偏置項均設為0。假設輸入的序列中除了的值為1以外，其它輸入的值均為0，則根據前一篇講解RNN的原理內容，可以知道：

最終可以得到，神經網路的輸出是關於權重矩陣W的指數函式。當W的值大於1時，隨著n的增加，神經網路最終輸出的值也成指數級增長，而當W的值小於1時，隨著n的值增加，神經網路最終的輸出則會非常小。這兩種結果分別是導致梯度爆炸和梯度消失的根本原因。

從上面的例子可以看到，迴圈神經網路中梯度消失和梯度爆炸問題產生的根本原因，是由於引數共享導致的。

2.長期依賴問題的優化

對於梯度爆炸的問題，一般來說比較容易解決。我們可以用一個比較簡單的方法叫做“梯度截斷”，“梯度截斷”的思路是設定一個閾值，當求得的梯度大於這個閾值的時候，就使用某種方法來進行干涉，從而減小梯度的變化。還有一種方法是給相關的引數新增正則化項，使得梯度處在一個較小的變化範圍內。

梯度消失是迴圈神經網路面臨的最大問題，相較於梯度爆炸問題要更難解決。目前最有效的方法就是在模型上做一些改變，這就是我們下一節要介紹的門控迴圈神經網路。本篇主要介紹了RNN的一些常用的迴圈網路結構，以及長期問題和如何優化。下一篇我們將介紹基於門控制的迴圈神經網路，也就是大家常見的LSTM以及GRU模型原理。

• 參考文獻

[1]BiDirectional_Recurrent_Neural_Networks_For_Speech_Recognition,Mike Schuster.

[2]Recursive Deep Models for Semantic Compositionality Over a Sentiment Treebank

歡迎大家關注我們的網站和系列教程：http://panchuang.net/ ，學習更多的機器學習、深度學習的知識！