轉載請註明出處。

隨機數

關於隨機數的定義：隨機數是專門的隨機試驗的結果。

當然這裡的隨機數說的是偽隨機數，是計算機通過某種計算生成的一個數。關於隨機數的意義及其價值，這裡就不多贅述，因為例子實在太多，筆者就用一個簡單的例子來講——計算π的近似值。

一、C/C++隨機數的產生

我們可以想象出，產生一個隨機數，就像當於在一片試驗田隨意地播撒種子，每個種子都會落到不同的地方，這樣就體現了隨機性。

C/C++是這樣產生隨機數的：
首先，我們要引用包含srand()（隨機數發生器初始化函式）、rand()（隨機數產生函式）函式的標頭檔案，這兩個函式都包含於常用標準函式庫，在C++中引用標頭檔案cstdlib（C中為stdlib.h）。

要想產生的隨機數不同，可以使用系統時間來初始化隨機數的發生。
這樣就需要引用包含時間函式的標頭檔案ctime（C中為time.h）。

程式碼可以寫成：

#include<iostream>
#include<ctime>     //包含時間的標頭檔案
#include<cstdlib>   //包含隨機數函式的標頭檔案
using namespace std;
int main()
{
    srand((unsigned)time(NULL));    
    //初始化隨機數的發生，使用時間函式並使其非負
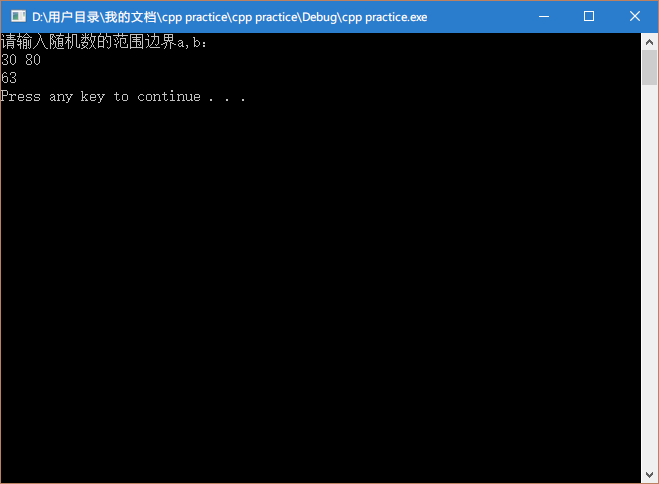
    int a = 0, b = 0;
    int
 
 i = 1, r = 0;
    cout << "請輸入隨機數的範圍邊界a,b：" << endl;
    cin >> a >> b;
    while (i) {
        r = rand() % (b - a + 1) + a;   /*控制隨機數的範圍（簡單記為：取“區間長度+1”的模再+前端點值）*/
        cout << r << endl;
        --i;
    }
    system("pause");
    return 0;
}

若想產生隨機小數
可以修改變數：

float r;
r=rand()%(b-a+1)+a+(float)rand()%1000/1000.0
//隨機產生位數不定的小數

這裡有一個值得注意的地方，隨機數每次只能產生一個。如果需要用到不同的隨機數，那麼產生的隨機數的函式要放在迴圈裡面，這樣每次執行程式的時候，隨機數才會隨著迴圈的改變而隨機改變。

二、計算π的近似值

隨機數的應用很廣，估算π的近似值也是很重要的應用。
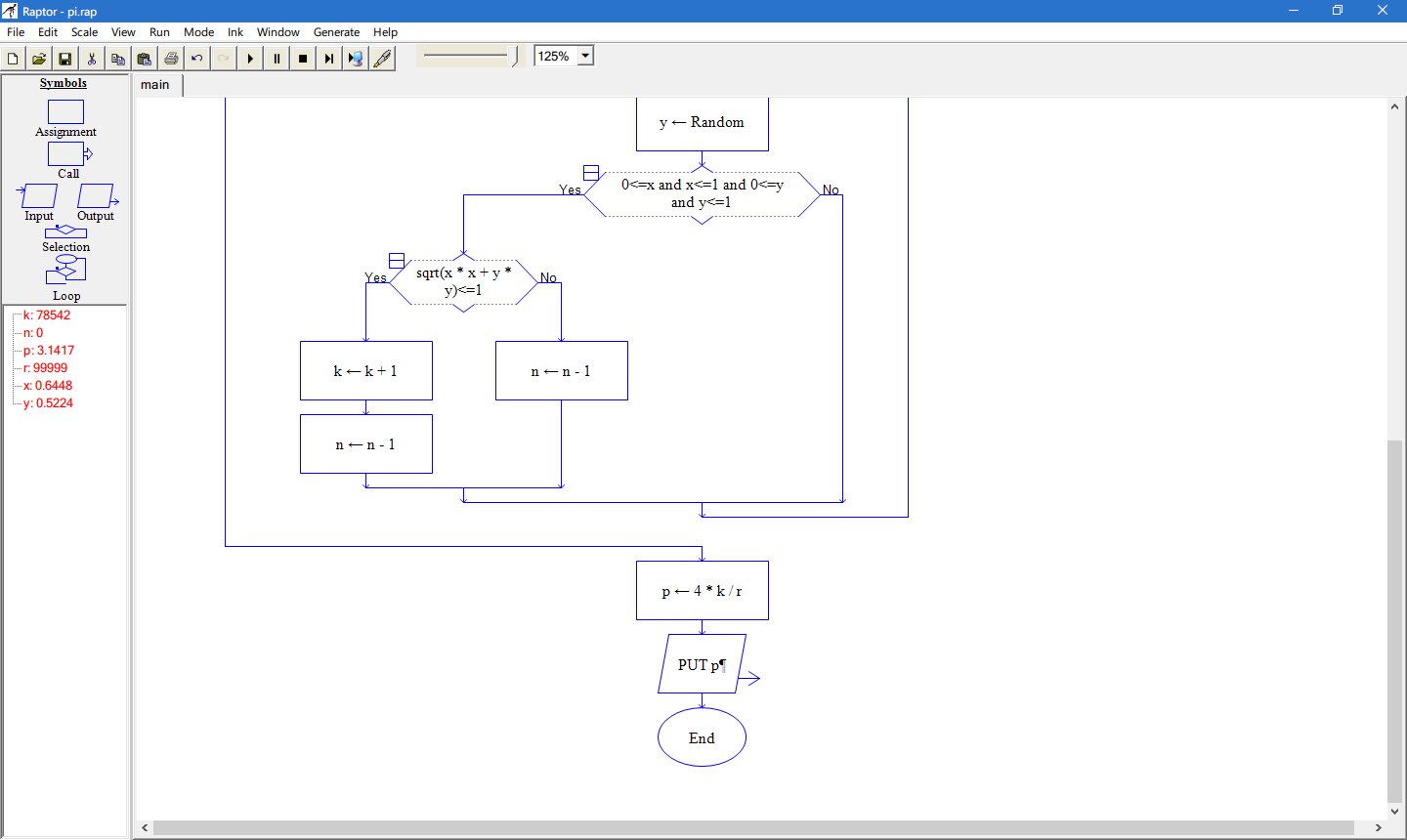
這裡使用的是最常用的撒豆子演算法：
方便計算，這裡用單位圓，取r=1，
由圓的面積除以正方形的面積 πr²/4r² = π/4————————–(1)

往正方形內撒豆子，所以把正方形面積看成beans，撒進1/4圓的豆子看成k，即1/4圓的面積。

這樣由(1)就得到一條等式 4k/b=π

用raptor進行視覺化演算法設計：

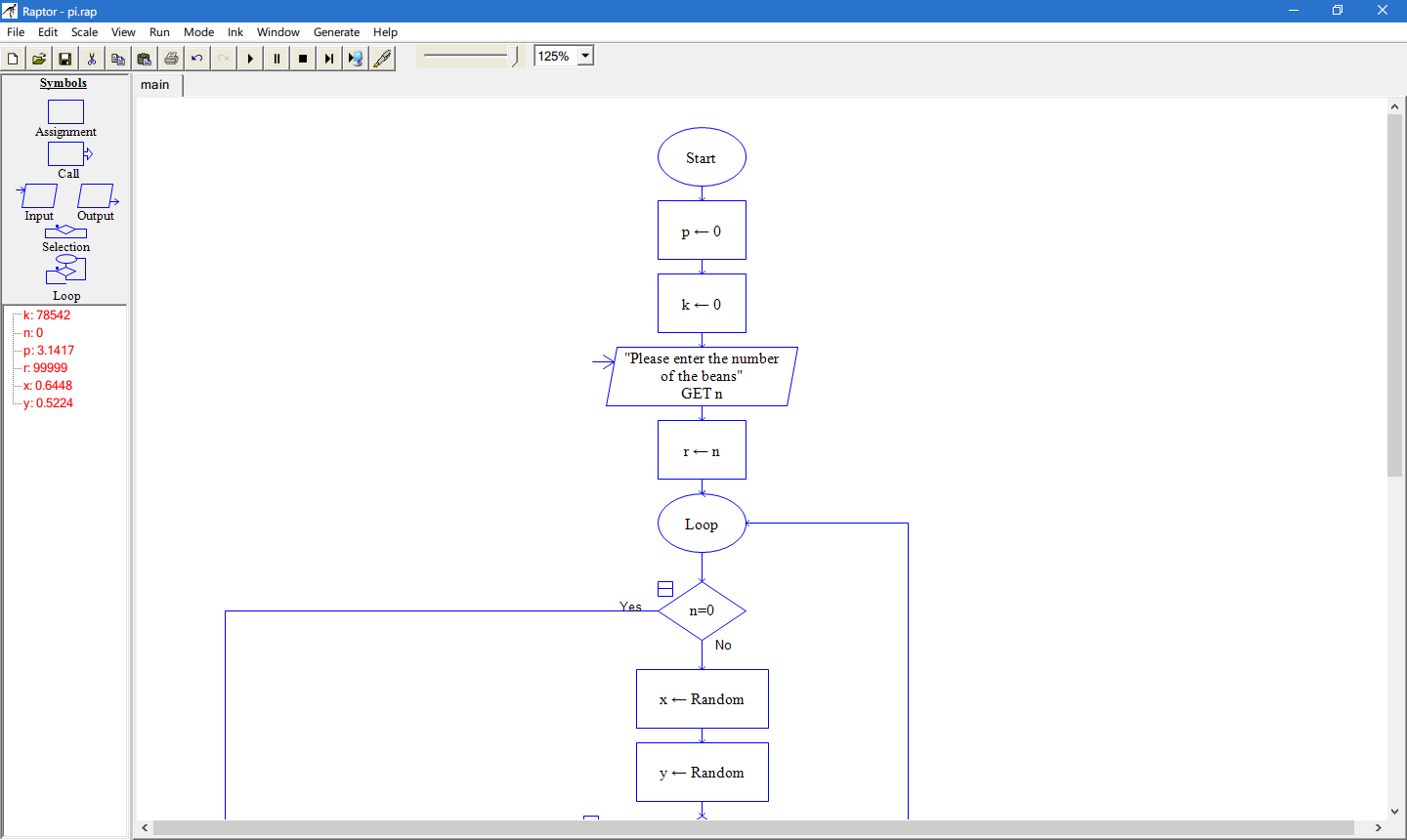
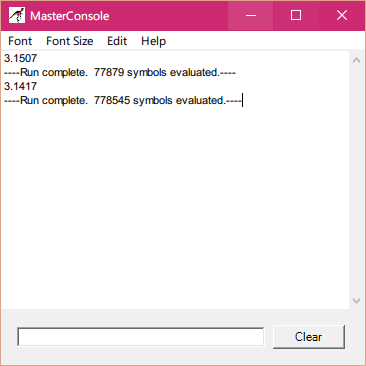
這裡先是用了99、999、9999三個數字的豆子進行計算，結果也是差別很大，得不到理想的圓周率。
如果按照這樣的演算法進行更大數字的計算，耗時會更久。

下面是C++的描述：

#include<iostream>
#include<iomanip>
#include<cstdlib>
#include<ctime>
#include<cmath>     //包含開平方sqrt()函式的標頭檔案
using namespace std;
int main()
{
    srand((unsigned)time(NULL));
    int k = 0;
    int n = 0, beans = 0;
    double pi;
    double x = 0, y = 0;

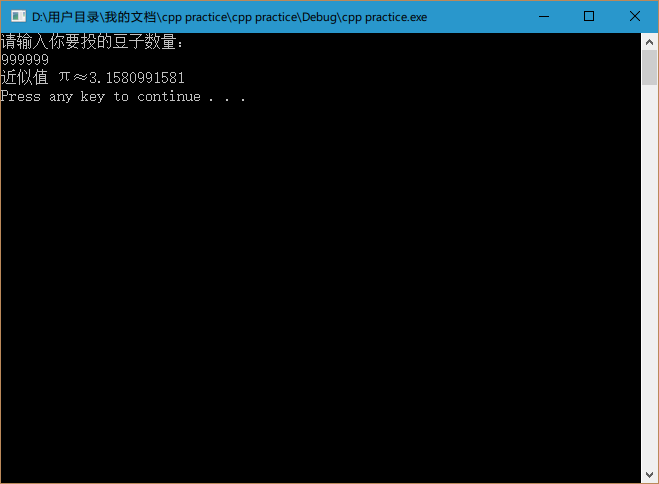
    cout << "請輸入你要投的豆子數量：" << endl;
    cin >> n;
    beans = n;
    do 
    {
        x = rand() % 2 + 0 + (double)(rand() % 1000) / 1000.0;
        y = rand() % 2 + 0 + (double)(rand() % 1000) / 1000.0;

        if (0 <= x&&x <= 1 && 0 <= y&&y <= 1) 
        {
            if (sqrt(x*x + y*y) <= 1) 
            {
                ++k;
                --n;
            }
            else --n;
        }
    } while (n > 0);
    pi = 4.0 * k / beans;
    cout << "近似值 π≈" << setiosflags(ios::fixed) << setprecision(10) << pi << endl;
    system("pause");
    return 0;
}

執行結果比較靠近實際情況：

小結：學習隨機數是一個比較有樂趣的過程，尤其是自己摸索的過程，是充滿樂趣的。

隨機數需要注意應用，比如用系統時間進行隨機數的生成、產生某一範圍的隨機數以及產生小數隨機數等等。收穫也是很大的。