首先要差分+離散化。
然後就是求形如ABA的串有多少，其中B的長度確定為k。
我們用到了設定關鍵點的思想。我們列舉A的長度L。然後在\(1,1+L,1+L*2,1+L*3。。。\)設定關鍵點。然後我們列舉這些關鍵點，試圖求出跨過這個關鍵點的長度為L的在B左邊的A有多少個。
可以證明這樣可以做到不重不漏，因為A的長度為L至少跨過一個關鍵點。
然後這個點的貢獻就怎麼算？我們先處理出字尾陣列。然後對列舉的關鍵點i和i+L+k求LCP和LCS。貢獻就是(min(LCP,L)+min(LCS,L)-1)-L+1。為什麼是這個呢？
當K=4，L=3時，如圖
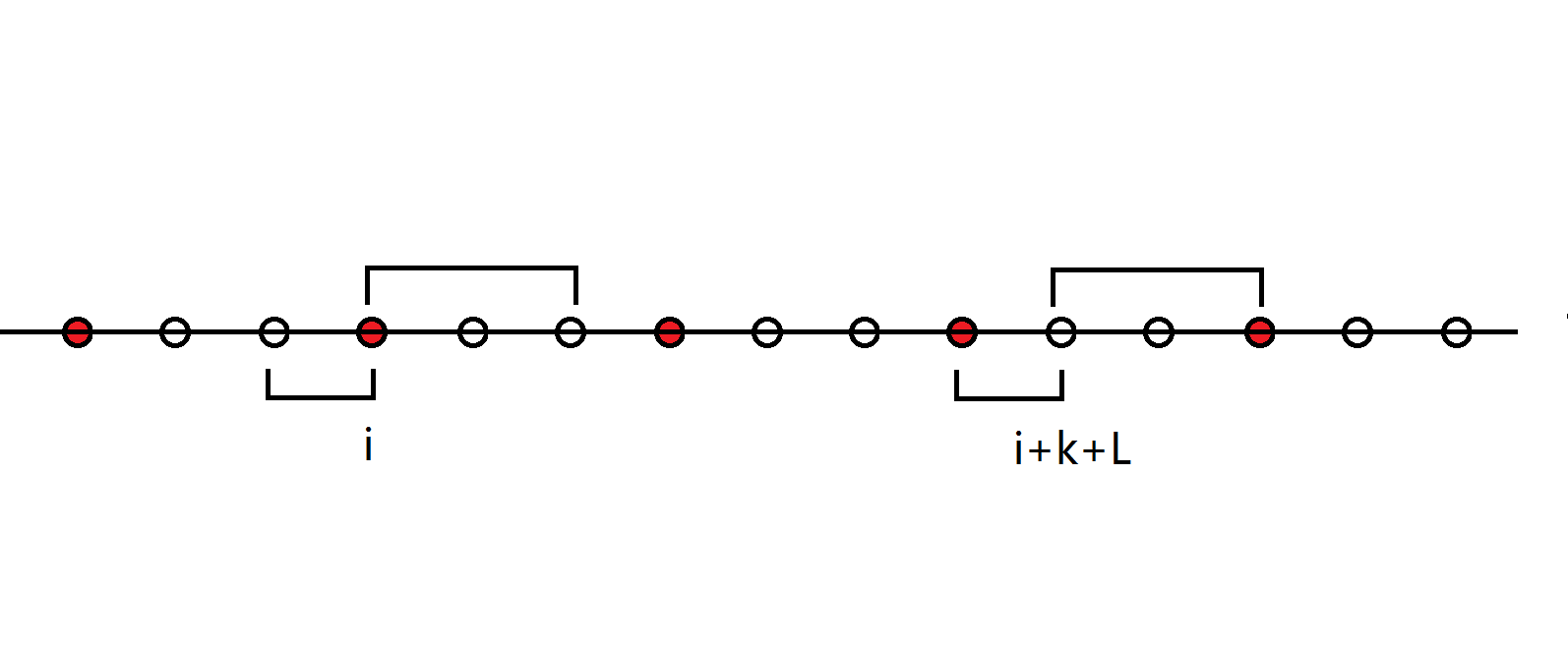實際上我們是確定了左邊A的區間就是\([i-LCP+1,i+LCS-1]\)

#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
#include<algorithm>
using namespace std;
const int N=100100;
int ans,n,a[N],b[N],k;
struct SA{
    int c[N],x[N],y[N],m,sa[N],rk[N],height[N],mn[N][20],s[N];
    void get_sa(){
        for(int i=1;i<=m;i++)c[i]=0;
        for(int i=1;i<=n;i++)c[x[i]=s[i]]++;
        for(int i=1;i<=m;i++)c[i]+=c[i-1];
        for(int i=n;i>=1;i--)sa[c[x[i]]--]=i;
        for(int k=1;k<=n;k<<=1){
            int num=0;
            for(int i=n-k+1;i<=n;i++)y[++num]=i;
            for(int i=1;i<=n;i++)if(sa[i]>k)y[++num]=sa[i]-k;
            for(int i=1;i<=m;i++)c[i]=0;
            for(int i=1;i<=n;i++)c[x[i]]++;
            for(int i=1;i<=m;i++)c[i]+=c[i-1];
            for(int i=n;i>=1;i--)sa[c[x[y[i]]]--]=y[i],y[i]=0;
            for(int i=1;i<=n;i++)swap(x[i],y[i]);
            x[sa[1]]=1;num=1;
            for(int i=2;i<=n;i++)
                x[sa[i]]=(y[sa[i]]==y[sa[i-1]]&&y[sa[i]+k]==y[sa[i-1]+k])?num:++num;
            if(n==num)break;
            m=num;
        }
    }
    void get_height(){
        int k=0;
        for(int i=1;i<=n;i++)rk[sa[i]]=i;
        for(int i=1;i<=n;i++){
            if(rk[i]==1)continue;
            if(k)k--;
            int j=sa[rk[i]-1];
            while(i+k<=n&&j+k<=n&&s[i+k]==s[j+k])k++;
            height[rk[i]]=k;
        }
    }
    void pre_work(){
        for(int i=1;i<=n;i++)mn[i][0]=height[i];
        int len=log2(n);
        for(int j=1;j<=len;j++)
            for(int i=1;i+(1<<j)-1<=n;i++)
                mn[i][j]=min(mn[i][j-1],mn[i+(1<<j-1)][j-1]);
    }
    int getlcp(int l,int r){
        if(l>r)swap(l,r);
        l++;
        int len=log2(r-l+1);    
        return min(mn[l][len],mn[r-(1<<len)+1][len]);
    }
}A,B;
int read(){
    int sum=0,f=1;char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9'){sum=sum*10+ch-'0';ch=getchar();}
    return sum*f;
}
int main(){
    n=read();k=read();
    for(int i=1;i<=n;i++)a[i]=read();
    for(int i=1;i<n;i++)a[i]=a[i+1]-a[i],b[i]=a[i];
    n--;
    sort(b+1,b+1+n);
    int tot=unique(b+1,b+1+n)-b-1;
    for(int i=1;i<=n;i++)a[i]=lower_bound(b+1,b+1+tot,a[i])-b;
    for(int i=1;i<=n;i++)A.s[i]=a[i],B.s[i]=a[n-i+1];
    A.m=B.m=51000;
    A.get_sa();A.get_height();A.pre_work();
    B.get_sa();B.get_height();B.pre_work();
    for(int i=1;i<=n;i++)
        for(int j=1;j+i+k<=n;j+=i)
            ans+=max(min(i,A.getlcp(A.rk[j],A.rk[j+i+k]))+min(i,B.getlcp(B.rk[n-j+1],B.rk[n-(j+i+k)+1]))-1,i-1)-(i-1);
    printf("%d",ans);
    return 0;
}