Discrete Difference Equation Prediction Model (DDEPM)

離散差分方程預測模型從灰度預測模型（grey prediction model）衍生出來，可以用於預測序列的發展趨勢。

DDEPM過程

DDEPM的流程如下圖所示

其中 $x^{\left(0\right)}$

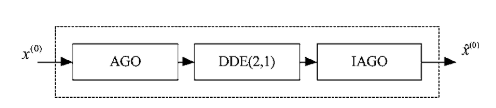
x^{(0)} 表示原始的序列， $x^{(1)}$

表示DDEPM預測值。AGO表示累加生成器（Accumulated Generating Operation）用於預處理原始序列 $x^{(0)}$

，把 $x^{(0)}$轉變成指數增長的序列。對原始序列應用一次AGO（1-AGO）就足夠生成一個指數增長序列。接下來構造一個單一變數的二階離散差分方程（DDE(2,1)）來擬合1-AGO生成的序列。通過DDE(2,1)可以預測序列中未知的元素值。因為DDE(2,1)預測的是AGO生成的序列，因此需要把預測結果還原，方法就是IAGO (Inverse Accumulated Generating Operation)。最後得到的就是原始序列的預測結果。

（1）獲取n個原始序列資料

$x^{(0)} = \{ x^{(0)}(1), x^{(0)}(2), x^{(0)}(3), \cdots, x^{(0)}(n) \} \quad n \in Z \tag{1}$
其中 $x^{(0)}$表示有n個元素的元素序列， $x^{(0)}(n)$表示原始序列的第n個元素。

（2）AGO

生成指數增長序列
$x^{(1)} = \{ x^{(1)}(1), x^{(1)}(2), x^{(1)}(3), \cdots, x^{(1)}(n) \} \quad n \in Z \tag{2}$
其中
$x^{(p)} = \sum_{i=1}^{p}x^{(0)}(i), \quad p=1,2,\cdots,n$

只對原序列進行一次AGO操作，因此稱 $x^{(1)}$為1-AGO序列。

因為要生成指數增長序列，所以原序列不能有負數元素，否則上述公式不能生成指數增長序列。

（3）DDE(2, 1)

使用單一變數的二階離散差分公式生成DDE(2, 1)來擬合1-AGO序列
$x^{(1)}(p+2) + a \cdot x^{(1)}(p+1) + b \cdot x^{(1)}(p) =0 \tag{3}$
其中a和b是係數，為了確定a和b，我們使用最小二乘法。我們把公式（3）重寫成
$\begin{bmatrix} -x^{(1)}(p+1) & -x^{(1)}(p) \end{bmatrix} \begin{bmatrix} a \\ b \end{bmatrix} = \begin{bmatrix} x^{(1)}(p+2) \end{bmatrix} \tag{4}$
讓 $p=1,2,\cdots,n-2$，接著公式（4）變為
$\begin{bmatrix} -x^{(1)}(2) & -x^{(1)}(1) \\ -x^{(1)}(3) & -x^{(1)}(2) \\ \vdots & \vdots \\ -x^{(1)}(n-1) & -x^{(1)}(n-2) \end{bmatrix} \begin{bmatrix} a \\ b \end{bmatrix} = \begin{bmatrix} x^{(1)}(3) \\ x^{(1)}(4) \\ \vdots \\ x^{(1)}(n) \end{bmatrix} \tag{5}$

相關推薦