求圖中最短路徑演算法之Dijkstra演算法——C++實現並優化
阿新 • • 發佈:2019-01-05
Dijkstra演算法是一種比較經典的求圖中最短路徑演算法,它是一種貪心演算法,可以求出從源節點到圖中其他所有節點的最短路徑。適用範圍:用於求有向或無向加權圖中兩點間的最短路徑,其中邊的權值不能為負。
最近重新學習了該演算法,並用C++將其實現,同時對程式碼進行了優化,優化思路如下:
一般的Dijkstra演算法實現程式碼,在每次將節點新增到S集合之前,都要在所有節點中進行搜尋,找出代價最小的節點進行新增。這種方法效率低下,我們可以發現,有兩類節點不是候選節點:1.已經新增到S集合中的節點;2.到源節點代價為無窮的節點。基於這個原因,我將新增到S集合的候選節點儲存在一個連結串列中,並動態的更新,以達到提升程式效率的目的。
由於Dijkstra演算法比較經典,在此不再贅述。下面給出原始碼。
輸入
第一行輸入三個整數n,m,s,分別表示節點個數,邊條數,源節點;接下來輸入m行,每一行輸入三個整數u,v,w,分別表示一條邊的起點,終點,權值;為了便於程式的除錯,可以從檔案中讀取資料;輸出
輸出從源節點到其他節點的最短路徑以及最小代價,如果不存在則輸出:No path;原始碼:
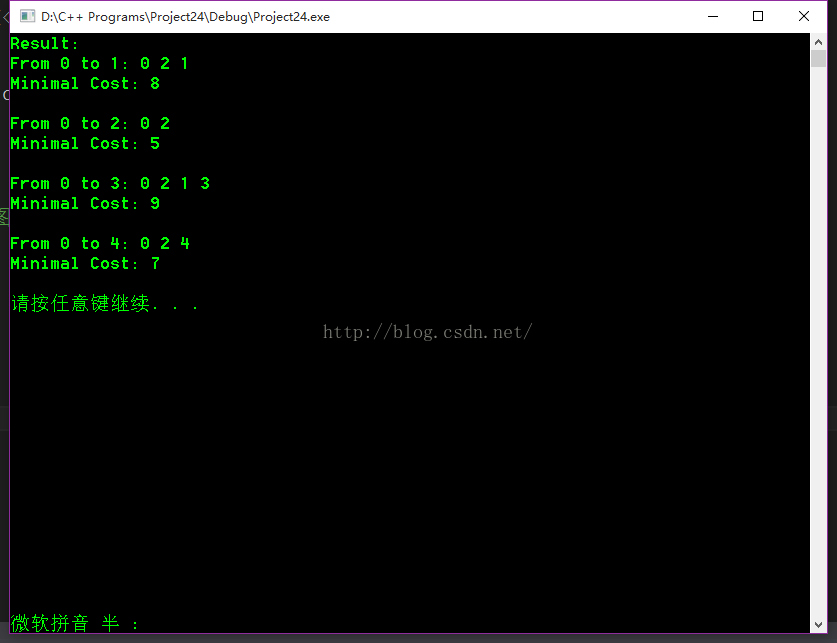
當用Dijkstra演算法求兩點間的最短路徑時,可以在S集合中添加了終節點後就終止程式,從而提高程式效率。 演算法測試圖:#include <iostream> #include <fstream> #include <vector> #include <list> using namespace std; //鄰接表中節點,每個節點與該節點對應的索引號指定一條邊 struct Node { int u; //邊終點節點號 int w; //邊權值 Node(int a, int b) :u(a), w(b){} }; struct Record { int pre; //路徑中當前節點的前一節點 int cost; //當前節點到源節點的最短路徑代價 }; int n, m, s; //n表示圖中節點個數,m表示圖中邊數,s表示源節點 vector<list<Node>> Adj; //圖的鄰接表 vector<Record> Path; //採用雙親表示法儲存源節點到其他所有節點的最短路徑資訊 void Dijkstra() { vector<bool> isUsed(n, false); //向量某索引號對應的值為true,表示該索引號對應的節點 //在S集合中 list<int> Assi; //Assi中儲存著當前的候選節點 Path.assign(n, Record()); //路徑資訊初始化 for (int i = 0; i < n; i++) { Path[i].pre = i; Path[i].cost = INT_MAX; } isUsed[s] = true; for (auto it = Adj[s].begin(); it != Adj[s].end(); it++) { Path[it->u].pre = s; Path[it->u].cost = it->w; Assi.push_back(it->u); } while (!Assi.empty()) { list<int>::iterator It; int minCost = INT_MAX; //從Assi中選擇代價最小的節點加入到S集合中 for (auto it = Assi.begin(); it != Assi.end(); it++) { if (minCost > Path[*it].cost) { minCost = Path[*it].cost; It = it; } } int u = *It; Assi.erase(It); isUsed[u] = true; //對與選中節點直接相連,並且不在S集合中的節點進行鬆弛操作 //同時更新Assi的內容 for (auto it = Adj[u].begin(); it != Adj[u].end(); it++) { if (isUsed[it->u]) continue; if (Path[it->u].cost == INT_MAX) Assi.push_back(it->u); if (Path[it->u].cost > minCost + it->w) { Path[it->u].cost = minCost + it->w; Path[it->u].pre = u; } } } } void Traverse(int k) { if (Path[k].pre == k) { cout << k; return; } Traverse(Path[k].pre); cout << " " << k; } void Print() { cout << "Result:\n"; for (int i = 0; i < n; i++) { if (i == s) continue; cout << "From " << s << " to " << i << ": "; if (Path[i].cost == INT_MAX){ cout << "No path\n\n"; continue; } Traverse(i); cout << endl; cout << "Minimal Cost: " << Path[i].cost << endl << endl; } } int main() { ifstream in("data.txt"); //從檔案中讀取圖的資訊 in >> n >> m >> s; int u, v, w; Adj.assign(n, list<Node>()); while (m--) { in >> u >> v >> w; Adj[u].push_back(Node(v, w)); } in.close(); Dijkstra(); Print(); system("pause"); return 0; }
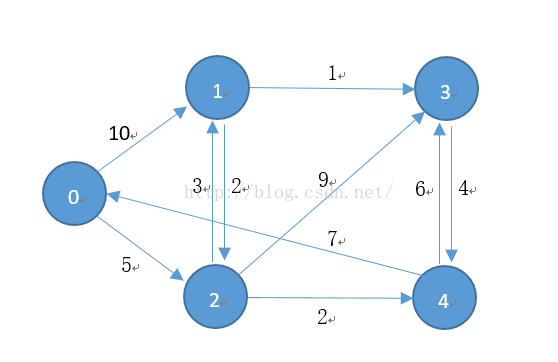 程式執行結果:
程式執行結果: