歡迎探討，如有錯誤敬請指正

如需轉載，請註明出處 http://www.cnblogs.com/nullzx/

1. 演算法的原理

以源點開始，以源點相連的頂點作為向外延伸的頂點，在所有這些向外延伸的頂點中選擇距源點最近的頂點(如果有多個距離最近的頂點，任意選擇一個即可)繼續向四周延伸（某個頂點被選作繼續延伸的頂點，則源點到它的最短距離就已經確定，我們也不再將其視為向外延伸的頂點了），如果在繼續延伸的過程中遇到了之前已延伸到的頂點，且當前這次延伸過程使其離源點更近，我們就修正這個距離，直到所有的頂點都被當做過繼續延伸的頂點，此時我們就得到了源點到其它各個頂點的距離。

2. 一個具體的例子

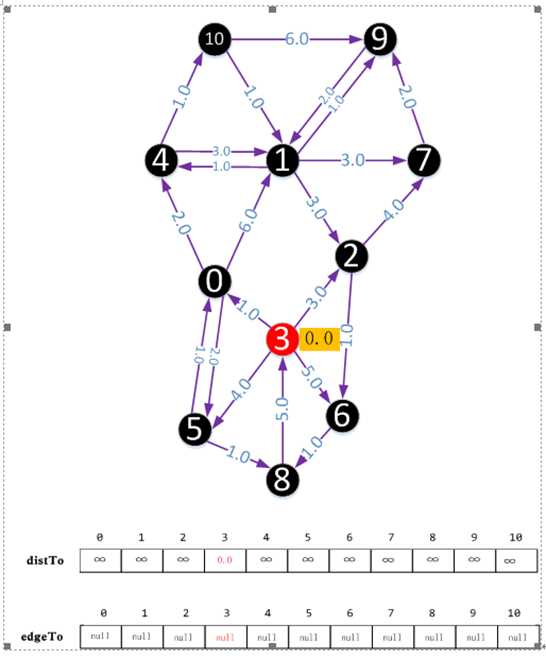
在下面的例子中，模擬了dijkstra演算法求解頂點3到其它各個頂點的最短距離。

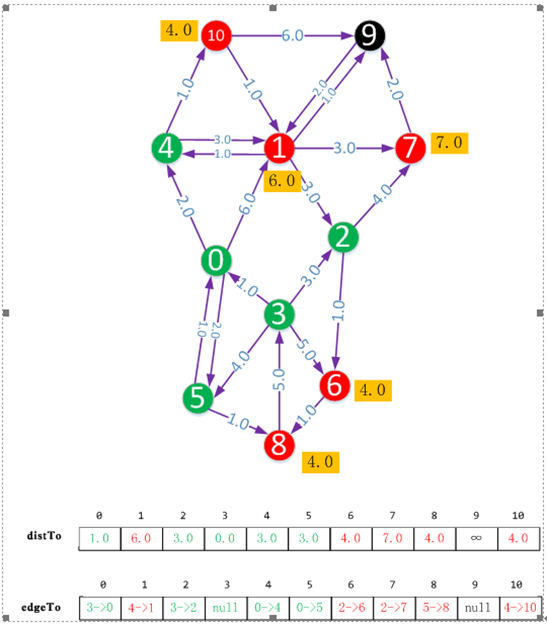
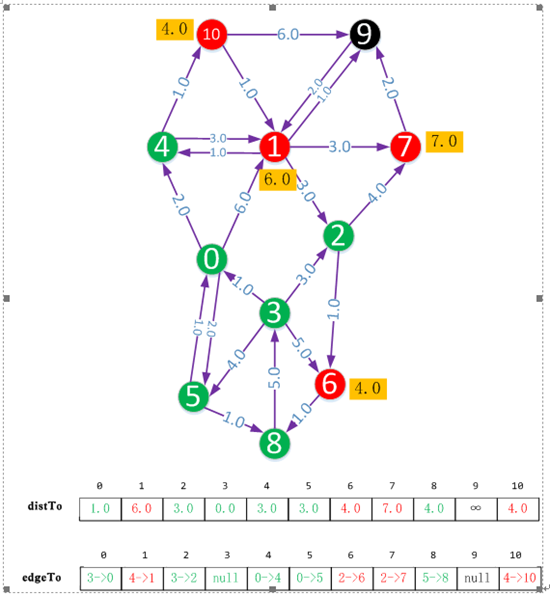
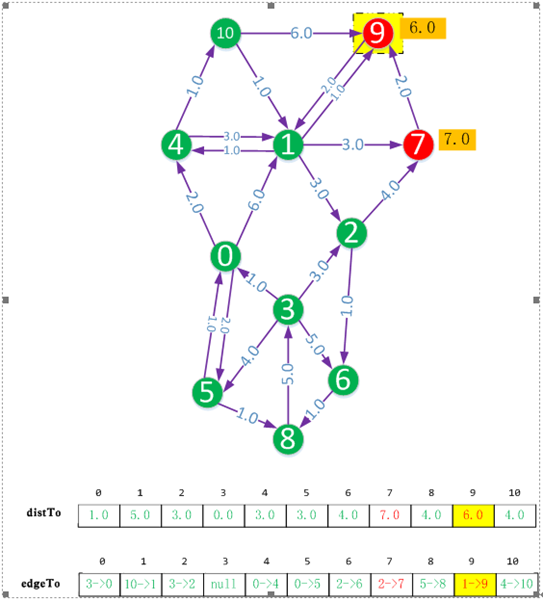
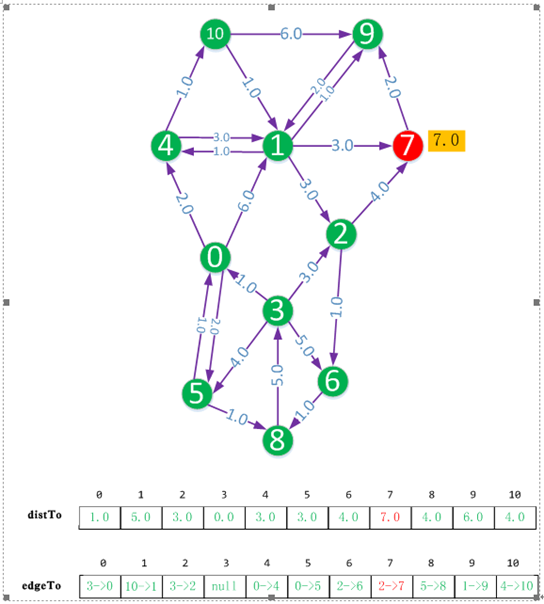
黑色的頂點表示沒有被延伸到的頂點，此時源點到它的距離為無窮。紅色頂點表示已被延伸到的頂點，紅色頂點旁的數字表示源點到它的距離。綠色頂點表示源點到該頂點的最短距離已確定。如果源點到某個頂點的距離被修正，我們將用黃色的方框將其標註。

distTo陣列表示源點（下圖中源點為頂點3）到各個頂點的距離，其中綠色的表示最短距離，紅色表示這個距離是否是最短距離還未確定。

edgeTo陣列表示源點（下圖中源點為頂點3）到各個頂點的路徑，其中綠色的表示最短距離路徑已確定，紅色表示這個路徑是否是最路徑離還未確定。edgeTo[i]表示經過頂點i的上一個頂點。

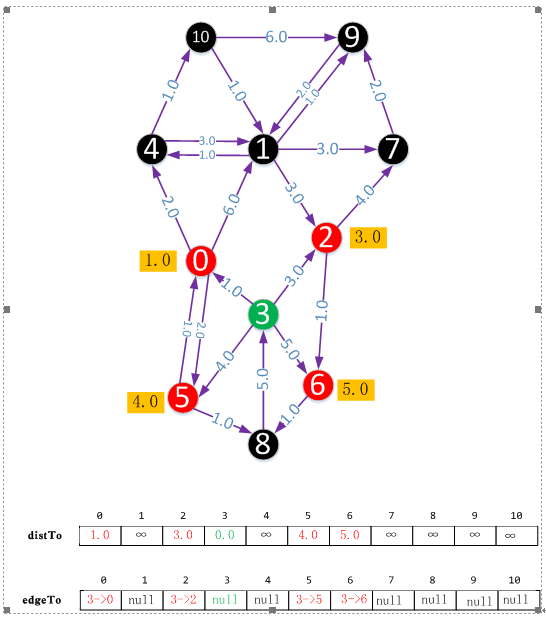
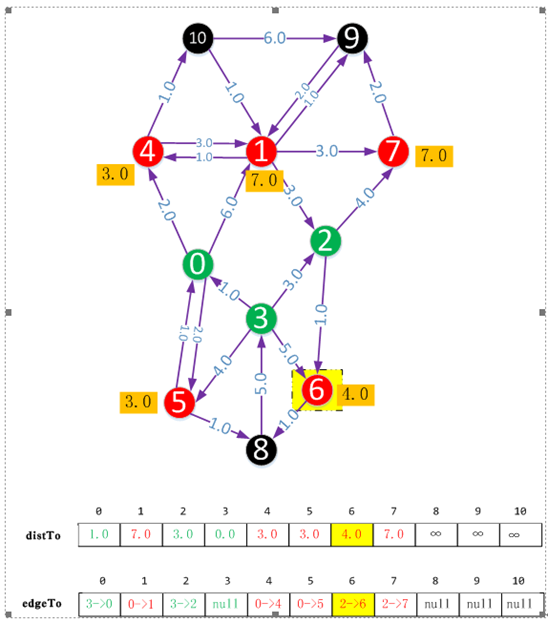
初始時，將源點看做向外延伸的頂點，它到自身的距離為0.0。每次向外延伸的過程中我們都會從紅色的頂點中選擇距離最近的頂點（如果距離最近的頂點有多個，則任意選擇一個）繼續向外延伸，然後把該頂點標註成綠色。

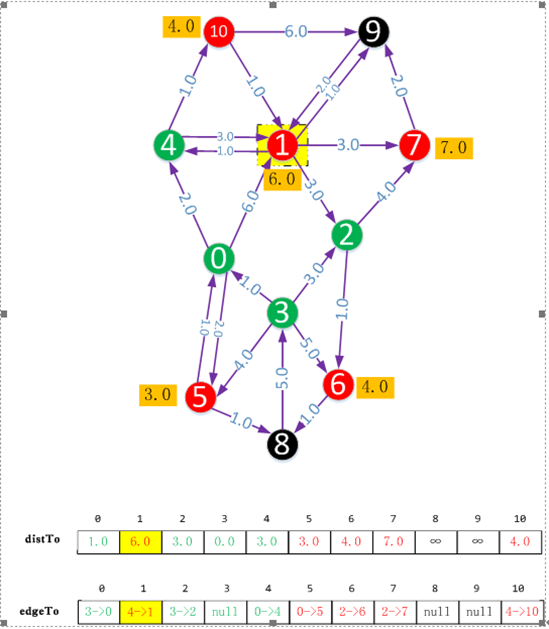
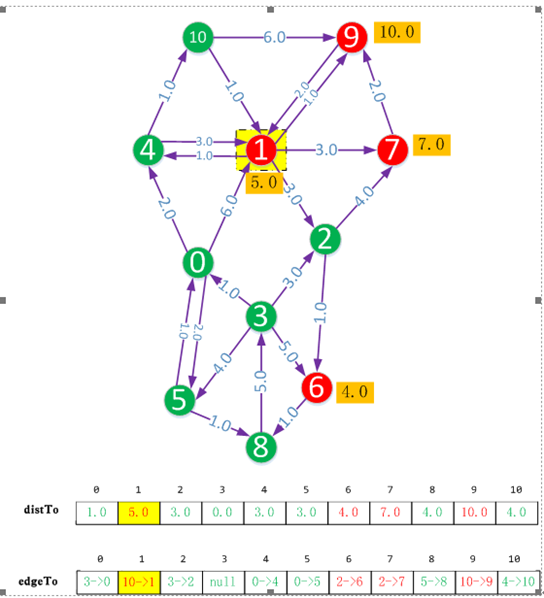
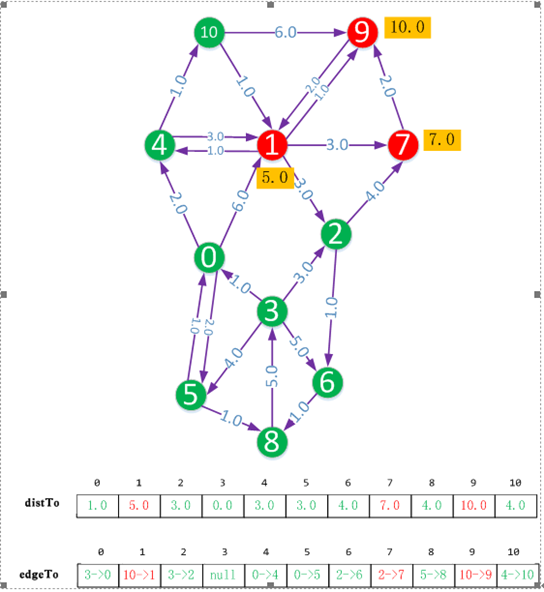
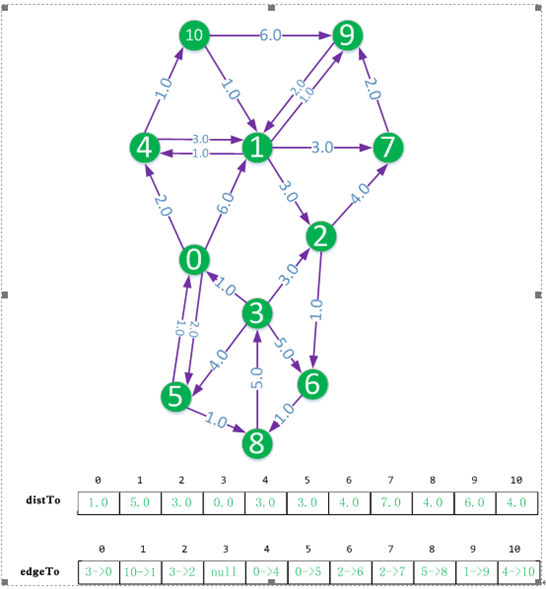
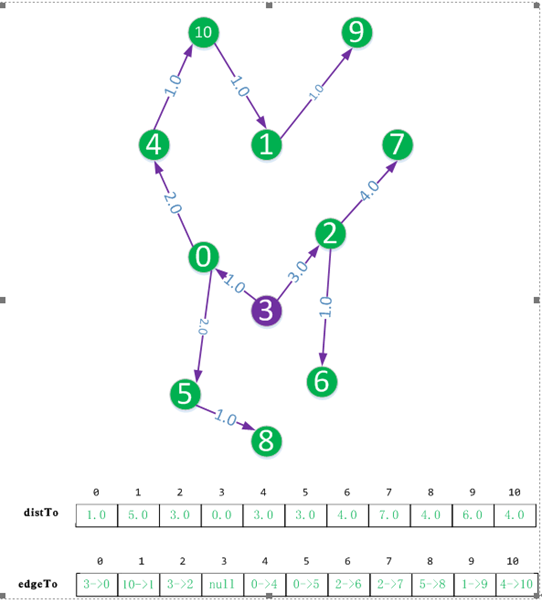
下面是源點到各個節點的最短路徑

最後我們從distTo和edgeTo陣列就可以找到最短的距離和路徑。

假設我們想得到源點，即頂點3，到頂點1的距離和路徑。

distTo[1]的值為5.0，說明最短距離為5.0。

edgeTo[1]說明到頂點1的上一個頂點為頂點10，edgeTo[10]說明到頂點10的上一個頂點為4，edgeTo[4]說明到頂點4的上一個頂點為頂點0,edgeTo[0]說明到頂點0的上一個頂點為頂點3。也就是路徑為3->0->4->10->1

3. 演算法的證明

要證明演算法的正確性，我們實際上需要證明：當從延伸頂點中選擇離源點最近的頂點繼續向外延伸時，源點到它的最短距離就已經確定了。

假設當前延伸頂點中最短的距離的頂點t，同時存在一條路徑從已訪問到的頂點k經過某些未知頂點x到達t的距離更小。

已知distTo[s->t] <= distTo[s->k]，

如果distTo[k->x]以及distTo[x->t]都大於零， 那麼

distTo[s->t] < distTo[s->k] + distTo[k->x] + distTo[x->t]

上述不等式必然成立，所以演算法的正確性得以證明。不等式成立的充分條件是distTo[k->x]以及distTo[x->t]都大於零，這也使我們得出了Dijistra演算法的適用情況：邊的權值都為非負值。

顯然，如果是求給定兩點s到t的最短距離，我們只需要在延伸的過程中將t作為繼續向四周延伸的頂點時停止演算法即可。

4. 演算法的實現

測試資料

8 15 4 5    0.35 5 4    0.35 4 7    0.37 5 7    0.28 7 5    0.28 5 1    0.32 0 4    0.38 0 2    0.26 7 3    0.39 1 3    0.29 2 7    0.34 6 2    0.40 3 6    0.52 6 0    0.58 6 4    0.93

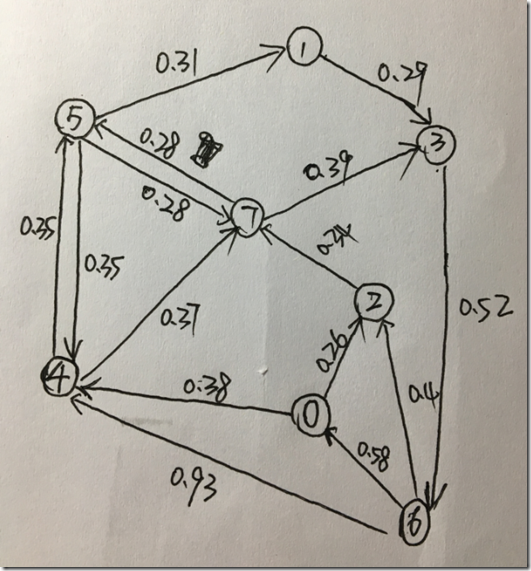輸出結果

原始碼

package datastruct;

import java.io.File;
import java.io.FileNotFoundException;
import java.io.FileReader;
import java.util.Arrays;
import java.util.LinkedList;
import java.util.List;
import java.util.PriorityQueue;

import datastruct.Graph.Edge;

public class Dijkstra {
	private double[] distTo;
	private Edge[] edgeTo;
	private PriorityQueue<DistTo> pq;
	private Graph g;
	private int s;
	
	//源點到頂點V的距離,
	public static class DistTo implements Comparable<DistTo>{
		public int idx;    //頂點的編號
		public double dist;//源點到頂點idx的短距離
		
		public DistTo(int v, double totalDist){
			this.idx = v;
			this.dist = totalDist;
		}

		@Override
		public int compareTo(DistTo that) {
			if(this.dist > that.dist){
				return 1;
			}else
			if(this.dist < that.dist){
				return -1;
			}else{
				return 0;
			}
		}
	}
	
	public Dijkstra(Graph g, int s){
		this.g = g;
		this.s = s;
		shortPath();
	}
	
	private void shortPath(){
		edgeTo = new Edge[g.V()];
		
		distTo = new double[g.V()];
		Arrays.fill(distTo, Double.POSITIVE_INFINITY);
		distTo[s] = 0.0;
		
		//如果到源點到頂點v的距離被多次修正，那麼優先佇列中就可能存在到頂點v的多個距離
		//所以以邊的個數作為優先佇列的最大長度，使用索引優先佇列是個更好的選擇
		pq = new PriorityQueue<DistTo>(g.E());
		
		pq.offer(new DistTo(s, 0.0));
		while(!pq.isEmpty()){
			DistTo v = pq.poll();//每次從優先佇列中找到最近的延伸頂點
			for(Edge e : g.adjEdge(v.idx)){//從與idx頂點的出邊繼續向下延伸
				int to = e.to();
				if(v.dist + e.weight() < distTo[to]){
					edgeTo[to] = e;//修正路徑
					distTo[to] = v.dist + e.weight();//修正距離
					pq.offer(new DistTo(to, distTo[to]));//修正後入列
				}
			}
		}
	}
	
	public double shortDistTo(int v){
		return distTo[v];
	}
	
	public List<Edge> shortPathTo(int v){
		LinkedList<Edge> stack = new LinkedList<Edge>();
		int to = v;
		if(distTo[to] == Double.POSITIVE_INFINITY){
			return stack;
		}
		
		while(edgeTo[to] != null){
			stack.push(edgeTo[to]);
			to = edgeTo[to].from();
		}
		return stack;
	}
	
	public static void main(String[] args) throws FileNotFoundException{
		File path = new File(System.getProperty("user.dir")).getParentFile();
		File f = new File(path, "algs4-data/tinyEWD.txt");
		FileReader fr = new FileReader(f);
		Graph g = new Graph(fr, true, true);
		System.out.println(g);
		
		Dijkstra dijkstra = new Dijkstra(g, 0);
		System.out.printf("%.2f\n", dijkstra.shortDistTo(6));
		List<Edge> shortPath = dijkstra.shortPathTo(6);
		for(Edge e : shortPath){
			System.out.println(e);
		}
	}
}

有關Graph類的實現可參照我技術部落格的另一篇文章：

5. 參考內容

[1]. 演算法（第4版）Robert Sedgewick 人民郵電出版社